- ... Gradienten1.1
- Die Numerik kennt raffiniertere
gradientenbasierte Verfahren als den
einfachen Gradientenanstieg.
Im Rahmen dieser Arbeit wird uns jedoch
statt der Frage, wie man einmal gewonnene Gradienten am
effizientesten zur Zielfunktionsmaximierung
einsetzt, vor allem der Entwurf angemessener
problemspezifischer Architekturen sowie unterschiedliche
Ansätze zur Gradientenberechnung
selbst interessieren.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nachbauen2.1
- Dazu
müßte man ja die
meisten Gewichte gleich Null setzen und ginge dabei der potentiell
ausschöpfbaren Möglichkeiten massiv paralleler Algorithmen verlustig.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Berechnungskomplexität2.2
- Pineda hat einen weiteren Algorithmus für
rekurrente Netze beschrieben, der, wie er selbst feststellt,
`einige der schlechtesten Eigenschaften beider Algorithmen
(BPTT und RTRL) besitzt' [72]. Sein
Verfahren benötigt
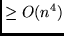 Speicherkomplexität und
Speicherkomplexität und
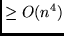 Zeitkomplexität, falls die Zahl der Zeitschritte
Zeitkomplexität, falls die Zahl der Zeitschritte
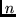 übersteigt.
übersteigt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Algorithmus2.3
- Kürzlich erfuhr ich, daß derselbe
Algorithmus auch von Williams in einem nicht öffentlich
angekündigten Report [148] beschrieben wurde, dessen
Inhalt in [152] erscheinen wird.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Ergebnissen2.4
- Giles,
Miller, Chen and Chen, Sun und Lee extrahieren aus
trainierten Netzen (mit Verbindungen zweiter Ordnung)
auch noch den zugehörigen minimalen endlichen
Automaten [29].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Gedächtnisstruktur3.1
-
Mit dem Ausdruck `differenzierbare Gedächtnisstruktur' ist
ein Speicher gemeint, dessen zeitveränderliche Inhalte
bezüglich aller Parameter, die das Systemverhalten steuern,
differenzierbar sind. Gleichzeitig sollte das Performanzmaß
bezüglich der Gedächtnisinhalte differenzierbar sein.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... geschaffen3.2
- Hier
sollte vielleicht angemerkt werden, daß neuronalen Netzen
bis vor kurzem gelegentlich vorgeworfen wurde, keinen Mechanismus
zur Variablenbindung anzubieten.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
kann4.1
- Es gibt Algorithmen für R-Lernen,
die keine derartigen Annahmen machen, z.B.
[7], [8],
[147], [6], [9],
[90], [140],
[97],
[51], [92].
Die theoretischen Grundlagen der meisten dieser Algorithmen
reichen allerdings höchstens in Spezialfällen aus, um im
asymptotischen Fall die
Konvergenz zu (sub)optimalen Lösungen zu beweisen.
Wir wollen uns hier
auf Algorithmen beschränken, die
aus bestimmten Voraussetzungen über Performanzmaß und
Architektur mathematisch sauber
ableitbar sind.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Rückkopplung4.2
-
Bei externer Rückkopplung können Ausgaben zu früheren
Zeitpunkten Einfluß auf spätere Eingaben nehmen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... an5.1
-
Das Konzept einer `Regularität' kleidet sich jedoch in viele
Gewänder. Um die Tatsache zu würdigen, daß es
nicht nur einen einzigen allgemein akzeptierten Ansatz
zur Definition `regulärer Struktur' gibt, beachte man,
daß algorithmische Informationstheorie
[43][17] reguläre Muster
in einer von statistischer Informationstheorie
[125] unterschiedlichen Weise definiert.
Die algorithmische Information eines Musters ist im
wesentlichen die Läge des kürzesten Programms, das das Muster
reproduzieren kann. Da es kein allgemeines Verfahren zum Finden
solch eines Programms gibt (im wesentlichen deswegen nicht,
weil keine obere Schranke für seine Laufzeit gefordert wird
 Halteproblem), wird
algorithmische Informationstheorie in der Regel nicht als
ein praktikables Werkzeug zur Entdeckung von Regularitäten
angesehen.
Halteproblem), wird
algorithmische Informationstheorie in der Regel nicht als
ein praktikables Werkzeug zur Entdeckung von Regularitäten
angesehen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Nebenbedingung5.2
- Der
Nebenbedingung (5.6) kommt eine entscheidende Rolle zu.
Beispiel:
Man betrachte vier 4-dimensionale Eingabevektoren
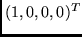 ,
,
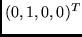 ,
,
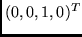 ,
,
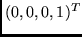 .
Wir nehmen an, daß
die ersten beiden Eingabemuster auf das 4-dimensionale
Ausgabemuster
.
Wir nehmen an, daß
die ersten beiden Eingabemuster auf das 4-dimensionale
Ausgabemuster
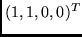 und die verbleibenden zwei Eingabemuster auf
und die verbleibenden zwei Eingabemuster auf
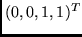 abgebildet werden. Dies liefert
zwar maximale Varianz 4,
maximiert jedoch nicht
die Zahl der verschiedenen
Musterklassifizierungen, und führt auch nicht zu lokaler
Repräsentation.
Die `bessere'
informationserhaltende (und Bedingung (5.6) erfüllende)
Abbildung, welche jedes Muster auf sich
selbst abbildet, besitzt lediglich Varianz 3.
abgebildet werden. Dies liefert
zwar maximale Varianz 4,
maximiert jedoch nicht
die Zahl der verschiedenen
Musterklassifizierungen, und führt auch nicht zu lokaler
Repräsentation.
Die `bessere'
informationserhaltende (und Bedingung (5.6) erfüllende)
Abbildung, welche jedes Muster auf sich
selbst abbildet, besitzt lediglich Varianz 3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ist5.3
- Eine
triviale Klassifikation, die alle Eingaben
auf denselben Repräsentationsvektor abbildet, wäre zwar
stets vorhersagbar, aber nicht informationstragend.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... minimieren5.4
-
Man könnte zusätzliche `Vorhersagenetzwerke'
einführen - eines, um
 aus
aus  vorherzusagen, und ein weiteres, um
vorherzusagen, und ein weiteres, um
 aus
aus  vorherzusagen.
Dann ließen sich Zielfunktionen zur Erzwingung wechselseitiger
Vorhersagbarkeit konstruieren (statt die im wesentlichen
gleichwertige Funktion
vorherzusagen.
Dann ließen sich Zielfunktionen zur Erzwingung wechselseitiger
Vorhersagbarkeit konstruieren (statt die im wesentlichen
gleichwertige Funktion 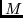 zu verwenden).
Dies würde die Allgemeinheit des Ansatzes allerdings nicht erhöhen, sondern
lediglich unnötige zusätzliche Komplexität nach sich ziehen.
zu verwenden).
Dies würde die Allgemeinheit des Ansatzes allerdings nicht erhöhen, sondern
lediglich unnötige zusätzliche Komplexität nach sich ziehen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... läßt6.1
-
Bisher haben wir von dieser MSE-Eigenschaft keinen
Gebrauch gemacht - alle vorangegangenen Kapitel verwendeten
MSE im wesentlichen zur Funktionsapproximation, nicht zur
Modellierung von Erwartungswerten.
Das Kreuzentropiemaß stellt
eine zum Erreichen desselben Ziels geeignete
Alternative dar.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... forschen6.2
- Die
`winner-take-all'-Netze erschienen vielen Forschern
noch nie als wirklich plausible
Kandidaten für die Modellierung interner Repräsentationen
biologischer Gehirne.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
zu6.3
- Definiert man eine sehr ähnliche Zielfunktion
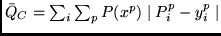 (basierend auf Absolutwerten statt MSE), so findet man
interessanterweise
(basierend auf Absolutwerten statt MSE), so findet man
interessanterweise
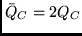 im Falle eines quasi-binären faktoriellen Codes.
im Falle eines quasi-binären faktoriellen Codes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wurde6.4
-
Alex Pouget wies darauf hin, daß für Zufallsvariablen
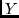 und
und 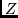 folgendes gilt:
folgendes gilt:
wobei 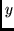 über alle möglichen Werte von
über alle möglichen Werte von 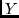 , und
, und
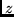 über alle möglichen Werte von
über alle möglichen Werte von 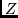 rangiert.
rangiert.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... reduzieren7.1
-
Aus der algorithmische Informationstheorie wissen wir natürlich,
daß sich wahrhaft
zufällige Sequenzen prinzipiell nicht signifikant
komprimieren lassen [17][43].
Bei der durch den trivialen Prediktor prozessierten Münzwurfserie
steckt die vermeintlich `hinwegkomprimierte'
Information in Wirklichkeit in den zur Rekonstruktion der
Serie erforderlichen, mit den unvorhergesagten Münzwurfresultaten
assoziierten Zeitrepräsentanten. Wahre Kompressionserfolge
lassen sich nur mit nicht zufälligen, `Regularitäten' enthaltenden
Sequenzen erzielen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... widerzuspiegeln7.2
- [76] beschrieb eine
alternative ad-hoc Methode zum Bau einer entfernt verwandten Hierarchie
im Kontext des R-Lernens.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Schmidhuber:90washington7.3
-
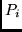 könnte aber auch ein beliebiger anderer adaptiver Mechanismus
zur Vorhersage von Sequenzeingaben sein.
So könnte man z.B. ein azyklisches BP-Netz und
den `Zeitfensteransatz' verwenden.
Mit dieser in ihren Möglichkeiten beschränkten
Methode bleibt die Anzahl der vergangenen Eingaben, die für
die Vorhersage der neuen Eingabe berücksichtigt werden können, konstant.
könnte aber auch ein beliebiger anderer adaptiver Mechanismus
zur Vorhersage von Sequenzeingaben sein.
So könnte man z.B. ein azyklisches BP-Netz und
den `Zeitfensteransatz' verwenden.
Mit dieser in ihren Möglichkeiten beschränkten
Methode bleibt die Anzahl der vergangenen Eingaben, die für
die Vorhersage der neuen Eingabe berücksichtigt werden können, konstant.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Zeitschritts7.4
-
Eine eindeutige Repräsentation der
seit dem letzten
unerwarteten Ereignis verstrichenen
Zeitspanne tut es genauso.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wird7.5
-
Im Gegensatz hierzu sind die von Mozer [61] zitierten
`reduzierten Beschreibungen' nicht eindeutig.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... minimieren7.6
- Diese für
überwachtes Lernen notwendige
Modifikation wurde von Pollack allerdings nicht berücksichtigt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
vorgeschlagenen7.7
-
In seiner Arbeit erwähnte Pollack
dieses Potential für lokale
Algorithmen nicht - der Fokus seiner
Untersuchungen war ein ganz anderer.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
anzupassen8.1
-
Wir können
Aussagen über den Effekt unserer eigenen Lernprozeduren
machen, wie beispielsweise in dem Satz ``Heute werde ich mich hinsetzen
und 20 japanische Wörter lernen.'' Wir reden nicht nur
darüber, wie wir lernen, sondern verfügen auch über die Fähigkeit,
unser Lernverhalten explizit zu ändern und den
Gegebenheiten der Umgebung anpassen.
Wir lernen beispielsweise, unsere eigenen Trainingsbeispiele auszusuchen.
Wir lernen, Einfluß darauf zu nehmen, welche Assoziationen
wir abspeichern.
Für viele Problemklassen
entwickeln wir spezifische interne Problemrepräsentationen
und effiziente Lernstrategien. Diese Strategien mögen
bestimmte Formen des `Analogielernens', `chunkings',
`one-shot'-Lernens, etc.
beinhalten. Es gibt jedoch Grund dafür, anzunehmen, daß
sich viele spezifische Lernstrategien nicht adäquat durch eine
dieser geläufigen Bezeichnungen beschreiben lassen.
Nach einigen Jahren der Selbstbeobachtung gelangte der Autor
zu der Überzeugung,
daß Prozesse für `Lernen lernen' bereits auf sehr niedrigem
kognitiven Niveau für das Skalierungsverhalten
großer Lernsysteme von essentieller
Bedeutung sind. Dieses Kapitel will seine Motivation
jedoch nicht aus den dubiosen introspektiven Erfahrungen
des Autors schöpfen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Schritte8.2
-
Intuitiv formuliert besteht
das ultimate Ziel `selbstreferentiellen'
und `introspektiven' maschinellen Lernens (so wie ich es sehe)
darin, einen sogenannten `Lernkeim' zu entwerfen.
Der `Keim' ist ein hypothetischer ursprünglich möglichst
einfacher, doch allgemeiner Lernalgorithmus für
realistische endliche `Hardware'. Einer gegebenen Umgebung
(welche die Lösung bestimmter spezifischer Probleme fordert)
ausgesetzt, soll der
Keim lernen, unter `optimaler' Ausnutzung der limitierten
Zeit- und Speicherressourcen sich
graduell selbst in `bootstrap'-Manier zu verfeinern und
sich auf typische Lernprobleme zu spezialisieren.
Der hypothetische Keim könnte dieses Ziel durch Sammlung
von Informationen über Beziehungen zwischen typischen Problemen
und zugehörigen effizienten Lösungsstrategien erreichen.
Das vorliegende Kapitel behauptet nicht, das ultimate Ziel zu
erreichen. Aus diesem Grunde ist das Wort
`selbstreferentiell' durchwegs zwischen Anführungsstriche gesetzt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
sind8.3
- Diese
gradientenbasierten `selbstreferentiellen'
Lernalgorithmen stellen einen Spezialfall allgemeinerer
`selbstreferentieller' Lernalgorithmen dar, wie sie in
[114] behandelt
werden.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ändern8.4
-
Bei den mir bekannten älteren Ansätzen zum maschinellen
Lernen lassen sich die adaptiven Komponenten der Algorithmen
ausschließlich durch vorverdrahtete Lernalgorithmen
ändern.
Lenats komplexes `symbolisches' EURISKO-System
stellt möglicherweise eine Ausnahme dieser Regel dar
(Lenat berichtet, daß sein System Heuristiken zur Auffindung
von Heuristiken fand [48]).
EURISKOs Mechanismus wurde allerdings häufig
wegen seiner Undurchsichtigkeit
kritisiert, sowie dafür,
daß er gelegentliche in ihrer Bedeutung
schwer einzuschätzende Eingriffe seitens
des Programmierers notwendig machte.
Das viel einfachere
`subsymbolische' System des vorliegenden Kapitels
ist dagegen höchst transparent,
verfügt über ein
klar definiertes Performanzmaß,
und erfordert keinerlei Interventionen eines externen Programmierers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Ver\-bin\-dungs\-adres\-se8.5
-
Man beachte die Notwendigkeit kompakter Adressierschemata.
Man könnte ja in Anlehnung an Architektur 1 aus Kapitel 3
auf den alternativen Gedanken kommen, einen Analyseknoten pro
Verbindung einzuführen, doch offensichtlich kann das nicht
funktionieren: Am Ende hätten wir immer mehr Gewichte als
Analyseknoten, und damit mehr Gewichte, als
adressiert werden könnten. `Selbstreferenz' wäre auf diese Weise
nicht möglich.
Es sollte jedoch angemerkt werden, daß das binäre Adressierungsschema
bei weitem nicht das kompakteste Schema darstellt. Im Prinzip
erlauben reelle Zahlen ja die Darstellung
unbeschränkter Informationsmengen durch eine einzige Zahl.
Daher ist es beispielsweise möglich, beliebige simultane
Gewichtsänderungen für alle Gewichte durch die
möglichen reellwertigen Aktivationen
eines einzelnen Knotens zu repräsentieren.
Unbegrenzte Präzision
ist jedoch unrealistisch für praktische Anwendungen.
Und der Zweck dieses Kapitels ist ja nicht
das Auffinden der kompaktesten `selbstreferentiellen'
Adressierungsmethode, sondern lediglich
wenigstens einer solchen Methode - welche als
Repräsentant vieler vergleichbarer Ansätze gesehen werden
sollte.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Speicherressourcen8.6
- Oder durch
eine gegebene, für begrenzte Zeit (während der sie nur einen endlichen
Teil ihres Bandes benutzen kann) operierende Turingmaschine
- oder durch einen gegebenen endlichen Automaten.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... identifizieren8.7
-
Es sollte erwähnt werden, daß
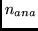 und
und 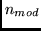 die Tendenz haben, mit
die Tendenz haben, mit
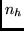 zu wachsen (falls beide nicht von vornherein groß genug
gewählt worden sind), da
zu wachsen (falls beide nicht von vornherein groß genug
gewählt worden sind), da
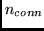 mit
mit
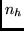 zunimmt.
zunimmt.
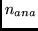 und
und 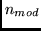 wachsen für große Netzwerke
jedoch viel langsamer als
wachsen für große Netzwerke
jedoch viel langsamer als
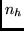 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ist8.8
- Einfachere Alternative ohne Fähigkeit zu expliziter Gewichtsänderung.
Da rekurrente Netze Allzweckmaschinen mit im wesentlichen
unbeschränkter Mächtigkeit sind, erlauben sie die Implementierung
beliebiger Algorithmen, einschließlich
durch Aktivationen statt durch Gewichte repräsentierter
Lernalgorithmen. Daher können wir im Prinzip ein einfacheres
`selbstreferentielles' System als dasjenige, auf welches sich
vorliegendes Kapitel konzentriert, mit einem
`konventionellen' rekurrenten Netz
ohne explizite Fähigkeit zur Eigengewichtsmodifikation
(mittels
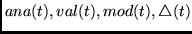 )
realisieren.
(So gesehen brauchen wir nur die erste der
in 8.1.2 aufgelisteten Modifikationen
konventioneller rekurrenter Netze zu behalten, nämlich die
Evalknoten.)
Dieses alternative Netz ist allerdings nicht imstande,
all seine adaptiven Parameter selbst zu kontrollieren.
)
realisieren.
(So gesehen brauchen wir nur die erste der
in 8.1.2 aufgelisteten Modifikationen
konventioneller rekurrenter Netze zu behalten, nämlich die
Evalknoten.)
Dieses alternative Netz ist allerdings nicht imstande,
all seine adaptiven Parameter selbst zu kontrollieren.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... einzeln8.9
-
Wie bereits verschiedentlich erwähnt, besteht dieses Kapitel
nicht auf Schemata zur Adressierung einzelner Gewichte.
Es existieren viele alternative Möglichkeiten,
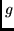 zu wählen und
die Gleichungen (8.3) und (8.5) entsprechend umzudefinieren.
zu wählen und
die Gleichungen (8.3) und (8.5) entsprechend umzudefinieren.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ist8.10
- Bei dem
alternativen Netzwerk aus
Fußnote
 (Abschnitt 8.1.3) würde dies darauf hinauslaufen,
die Aktivationen des Netzwerks am Ende eines Trainingsintervalls
nicht von neuem zu initialisieren.
Denn es könnte ja sein, daß
die Aktivationen einen nützlichen
`selbstreferentiellen' Lernalgorithmus darstellen.
(Abschnitt 8.1.3) würde dies darauf hinauslaufen,
die Aktivationen des Netzwerks am Ende eines Trainingsintervalls
nicht von neuem zu initialisieren.
Denn es könnte ja sein, daß
die Aktivationen einen nützlichen
`selbstreferentiellen' Lernalgorithmus darstellen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Kapitel8.11
-
Das Kapitel ist teilweise inspiriert durch ältere Ideen
zum Thema `Lernen lernen' -
[88] beschreibt einen `selbstreferentiellen'
genetischen Algorithmus sowie einge weitere `introspektive'
Systeme.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.