ÄQUIVALENZ VON $V_C$ UND $V - H$

Peter Dayan und Richard Zemel wiesen in persönlicher Kommunikation darauf hin, daß das Verfahren aus Abschnitt 6.3.6 und Vorhersagbarkeitsminimerung gemäß Abschnitt 6.4 für 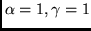$\alpha = 1, \gamma =1$ Kraft folgender Argumentation im wesentlichen äquivalent sind:

(6.11) läßt sich umschreiben als

$$\sum_{i,p} P(x^p) \left(y_i^p - E\left[y_i\vert\left\{y_j^p, j \neq i\right\}\right]\right)^2 =$$

$$\sum_{i,p} P(x^p) (y_i^p - \bar{y_i})^2 + \sum_{i,p} P(x^p) ... ...vert\left\{y_j^p, j \neq i\right\}\right]-\bar{y_i}\right)^2 -$$

$$-2\sum_{i,p} P(x^p) (y_i^p - \bar{y_i})\left(E\left[y_i\vert\left\{y_j^p, j \neq i\right\}\right]-\bar{y_i}\right).$$ (6.19)

Da

$$E\left[E\left[y_i\vert\left\{y_j, j \neq i\right\}\right]\right] = E\left[y_i\right] = \bar{y_i},$$

ist die dritte Zeile von (6.15) gleich

$$-2 COV\left[y_i,E\left[y_i\vert\left\{y_j, j \neq i\right\}\right]\right] .$$

Wie nun von Alex Pouget bemerkt wurde^6.4, gilt

$$COV\left[y_i,E\left[y_i\vert\left\{y_j, j \neq i\right\}\rig... ...E\left[y_i\vert\left\{y_j, j \neq i\right\}\right]\right] =$$

$$= \sum_{i,p} P(x^p) \left(E\left[y_i\vert\left\{y_j^p, j \neq i\right\}\right]-\bar{y_i}\right)^2$$ (6.20)

und damit auch

$$\sum_{i,p} P(x^p) \left(y_i^p - E\left[y_i\vert\left\{y_j^p,... ...\vert\left\{y_j^p, j \neq i\right\}\right]-\bar{y_i}\right)^2,$$

was zu zeigen war.

Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite