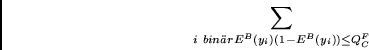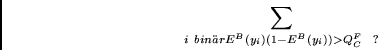Nächste Seite: ÄQUIVALENZ VON UND
Aufwärts: APPENDIX
Vorherige Seite: EINE NICHT PREDIKTORBASIERTE ZIELFUNKTION
Inhalt
Die Maximierung von
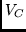 aus Abschnitt 6.4 ist äquivalent zur Maximierung von
aus Abschnitt 6.4 ist äquivalent zur Maximierung von
![\begin{displaymath}
Q_C = \sum_i \sum_p P(x^p) (P^p_i - y^p_i)^2 =
E [ E(y_i \mid \{y_k, k \neq i \}) - y_i ]^2,
\end{displaymath}](img643.png) |
(6.15) |
wobei 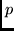 über alle unterschiedlichen Muster
(statt über alle Muster) rangiert, und
wobei wieder angenommen wird, daß
über alle unterschiedlichen Muster
(statt über alle Muster) rangiert, und
wobei wieder angenommen wird, daß
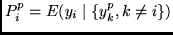 gilt.
gilt.
Definieren wir nun
 als das
als das 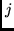 -te unterschiedliche Ereignis der
Form
-te unterschiedliche Ereignis der
Form
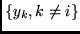 .
Es ist
.
Es ist
![\begin{displaymath}
E [ E(y_i \mid \{y_k, k \neq i \}) - y_i ]^2
\leq
E \left[ E(y_i) - y_i \right]^2,
\end{displaymath}](img645.png) |
(6.16) |
wobei das Gleichheitszeichen nur dann gilt, wenn der folgende
Ausdruck wahr ist:
Im Falle eines quasi-binären Codes läßt sich
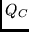 wie folgt umformen:
wie folgt umformen:
 |
(6.17) |
Ist der quasi-binäre Code faktoriell, so wird (6.13)
zu6.3
 |
(6.18) |
Die Maximierung von 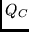 ermutigt quasi-binäre Codes.
Betrachten wir einen
quasi-binären faktoriellen Code
ermutigt quasi-binäre Codes.
Betrachten wir einen
quasi-binären faktoriellen Code 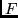 .
Es ist
.
Es ist
wobei zusätzliche hochgestellte Indices die Zugehörigkeit
zu einem bestimmten Code bezeichnen.
Jeder Code  mit
mit
kann aufgrund von (6.12) und (6.14)
keinen größeren Gesamtprediktionsfehler als 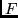 verursachen.
verursachen.
Was aber, wenn
Intuitiv scheint dies nahezulegen, daß die Codekapazität
die im Eingabeensemble enthaltene Entropie übersteigt,
was intra-repräsentationelle Redundanz nach sich
zieht, was wiederum kleineres
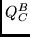 zur Folge hat. Es wurde zwar versucht, auch letzteren Fall
unter Ausnützung von
zur Folge hat. Es wurde zwar versucht, auch letzteren Fall
unter Ausnützung von
formal zu fassen, die
Vermutung 6.4.1 bleibt allerdings für den allgemeinen Fall
unbewiesen.




Nächste Seite: ÄQUIVALENZ VON UND
Aufwärts: APPENDIX
Vorherige Seite: EINE NICHT PREDIKTORBASIERTE ZIELFUNKTION
Inhalt
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite
![]() aus Abschnitt 6.4 ist äquivalent zur Maximierung von
aus Abschnitt 6.4 ist äquivalent zur Maximierung von
![]() als das
als das ![]() -te unterschiedliche Ereignis der
Form
-te unterschiedliche Ereignis der
Form
![]() .
Es ist
.
Es ist
![]() wie folgt umformen:
wie folgt umformen:
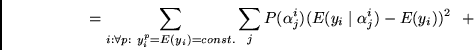
![\begin{displaymath}
+
\sum_{i~bin\uml {a}r} \sum_j P(\alpha^i_j)
\left[
\sum_{p...
...{p: y^p_i =0} P(x^p) (E(y_i \mid \alpha^i_j) - 0)^2
\right]
=
\end{displaymath}](img650.png)
![\begin{displaymath}
=
0~~ +
\sum_{i~bin\uml {a}r} \sum_j P(\alpha^i_j)
\left[
(...
...(y_i \mid \alpha^i_j))^2
\sum_{p: y^p_i =0} P(x^p)
\right]
=
\end{displaymath}](img651.png)
![\begin{displaymath}
=
\sum_{i~bin\uml {a}r} \sum_j P(\alpha^i_j)
\left[
(E(y_i ...
...y_i \mid \alpha^i_j))^2
(1- E(y_i \mid \alpha^i_j))
\right]
=
\end{displaymath}](img652.png)

![]() ermutigt quasi-binäre Codes.
Betrachten wir einen
quasi-binären faktoriellen Code
ermutigt quasi-binäre Codes.
Betrachten wir einen
quasi-binären faktoriellen Code ![]() .
Es ist
.
Es ist