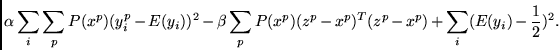Nächste Seite: ZUR VERMUTUNG 6.4.1
Aufwärts: APPENDIX
Vorherige Seite: APPENDIX
Inhalt
Untenstehendes Performanzmaß
beruht auf dem in Kapitel 5 ausgeführten Konzept
minimaler Bitentropiesummen.
Ist Code  binär, so
ist seine Bitentropiesumme
binär, so
ist seine Bitentropiesumme 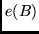 durch
durch
definiert.
Existiert ein faktorieller Code, so ist die Minimierung von
 über alle möglichen Binärcodes
über alle möglichen Binärcodes 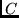 (wie in [5] ausgeführt)
äquivalent zur Auffindung eines der faktoriellen Codes.
Dies können wir ausnützen, um folgende zu maximierende Zielfunktion
für unsere Repräsentationsknoten zu definieren:
(wie in [5] ausgeführt)
äquivalent zur Auffindung eines der faktoriellen Codes.
Dies können wir ausnützen, um folgende zu maximierende Zielfunktion
für unsere Repräsentationsknoten zu definieren:
Dabei sei 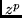 wie in Abschnitt 6.3.3 definiert, und
wie in Abschnitt 6.3.3 definiert, und
 und
und  stellen wieder positive Konstanten dar.
Der erste Term zwingt jeden Knoten dazu, in Antwort auf
ein bestimmtes Eingabemuster entweder an oder aus zu sein.
Der zweite Term erzwingt Reversibilität.
Der dritte Term zwingt den Mittelwert der Aktivationen
jedes Knotens, sich nahe bei entweder 0 oder 1 zu befinden.
Damit wird minimale Bitentropie ermutigt.
stellen wieder positive Konstanten dar.
Der erste Term zwingt jeden Knoten dazu, in Antwort auf
ein bestimmtes Eingabemuster entweder an oder aus zu sein.
Der zweite Term erzwingt Reversibilität.
Der dritte Term zwingt den Mittelwert der Aktivationen
jedes Knotens, sich nahe bei entweder 0 oder 1 zu befinden.
Damit wird minimale Bitentropie ermutigt.
Die Methode weist Verwandschaft zu einem älteren Ansatz
zur Auffindung nichtredundanter Codes auf [64].
Sie muß sich jedoch ebenfalls der in Abschnitt 6.3.7
erwähnten Kritik (betreffs des Parameterwahlproblems) beugen.




Nächste Seite: ZUR VERMUTUNG 6.4.1
Aufwärts: APPENDIX
Vorherige Seite: APPENDIX
Inhalt
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite
![]() binär, so
ist seine Bitentropiesumme
binär, so
ist seine Bitentropiesumme ![]() durch
durch