



Nächste Seite: MÄCHTIGKEIT DER KLASSE DER
Aufwärts: EIN `SELBSTREFERENTIELLES' REKURRENTES NETZ
Vorherige Seite: `KONVENTIONELLE' ASPEKTE DER ARCHITEKTUR
Inhalt
Dieser Abschnitt beschreibt bisher unspezifizierte Interpretationen
gewisser Ein- und Ausgaben, welche unser Netzwerk zum ersten
`selbstreferentiellen' Netzwerk mit expliziter Kontrolle über alle
sein Verhalten steuernde Parameter machen.
Da wir nicht alle potentiell nützlichen Arten der Selbstmodifikation
kennen können, und da geeignete
Selbstmodifikationsprozeduren beliebige Komplexität aufweisen
könnten, werde ich
die `selbstreferentiellen' Aspekte
dergestalt definieren, daß die
Selbstmodifikationsprozeduren
die Form beliebiger berechenbarer Abbildungen von
Algorithmuskomponenten und Performanzevaluationen
auf Algorithmusmodifikationen annehmen können
(modulo Zeit- und Speicherbegrenzungen).
Im folgenden werde ich vier unkonventionelle Aspekte auflisten.
Die resultierende Architektur sollte als Repräsentant
einer Vielzahl ähnlicher
Architekturen verstanden werden.
1. Das Netz `sieht' Performanzevaluationen.
Eine Teilmenge der Eingabeknoten,
die keine `normalen'
Eingabeknoten enthält, wird als Menge der
Evalknoten
(mit Kardinalität 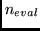 )
bezeichnet.
)
bezeichnet.
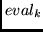 steht für den
steht für den 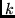 -ten Evalknoten.
Obwohl
diese Modifikation konventioneller Netze
im Vergleich mit den folgenenden Modifikationen relativ
einfach ist, repräsentiert sie doch den möglicherweise
bedeutsamsten Beitrag zur Erzielung
`selbstreferentieller' Architekturen, wie Fußnote
-ten Evalknoten.
Obwohl
diese Modifikation konventioneller Netze
im Vergleich mit den folgenenden Modifikationen relativ
einfach ist, repräsentiert sie doch den möglicherweise
bedeutsamsten Beitrag zur Erzielung
`selbstreferentieller' Architekturen, wie Fußnote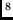 , Abschnitt 8.1.3
noch etwas detaillierter ausführen wird.
, Abschnitt 8.1.3
noch etwas detaillierter ausführen wird.
2. Jede adaptive Komponente des Netzes erhält eine Adresse.
Für jede Verbindung
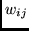 führen wir eine Adresse
führen wir eine Adresse
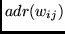 ein.
Dies wird dem Netz helfen, über seine eigenen Verbindungen
zu `reden', wie die nächsten beiden Punkte klarmachen
werden.
O.B.d.A. nehmen wir im folgenden an, daß
ein.
Dies wird dem Netz helfen, über seine eigenen Verbindungen
zu `reden', wie die nächsten beiden Punkte klarmachen
werden.
O.B.d.A. nehmen wir im folgenden an, daß
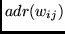 als Binärvektor repräsentiert sei (dies stellt jedoch
nur eine von vielen Möglichkeiten dar
als Binärvektor repräsentiert sei (dies stellt jedoch
nur eine von vielen Möglichkeiten dar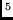 ).
).
3. Das Netz vermag all seine eigenen Gewichte zu analysieren.
Eine Untermenge der Nichteingabeknoten, welche keine
`normalen' Ausgabeknoten enthält, wird als
Analyseknoten bezeichnet.
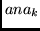 bezeichnet den
bezeichnet den 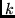 -ten von
-ten von 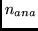 Analyseknoten.
Die Analyseknoten dienen dazu, sequentiell Verbindungen
anzusprechen, deren gegenwärtige Gewichte das Netzwerk `in Erfahrung
bringen möchte'.
Es bereitet keine Schwierigkeiten, die
Analyseknoten mit genügend Kapazität zur Adressierung
jeder beliebigen Verbindung auszustatten, einschließlich
jener Verbindungen, die zu Analyseknoten führen.
Dies läßt sich beispielsweise durch
Analyseknoten.
Die Analyseknoten dienen dazu, sequentiell Verbindungen
anzusprechen, deren gegenwärtige Gewichte das Netzwerk `in Erfahrung
bringen möchte'.
Es bereitet keine Schwierigkeiten, die
Analyseknoten mit genügend Kapazität zur Adressierung
jeder beliebigen Verbindung auszustatten, einschließlich
jener Verbindungen, die zu Analyseknoten führen.
Dies läßt sich beispielsweise durch
 |
(8.2) |
erreichen, wobei
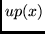 die kleinste ganze Zahl
die kleinste ganze Zahl 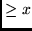 liefert.
Ein spezieller Eingabeknoten, der weder
`normaler' Eingabeknoten noch Evalknoten ist, wird mit
liefert.
Ein spezieller Eingabeknoten, der weder
`normaler' Eingabeknoten noch Evalknoten ist, wird mit 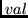 bezeichnet.
bezeichnet.
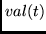 berechnet sich gemäß
berechnet sich gemäß
![\begin{displaymath}
val(1) = 0,~~\forall t\geq 1:~
val(t+1) = \sum_{i,j}g[ \Vert ana(t) - adr(w_{ij}) \Vert^2]w_{ij}(t),
\end{displaymath}](img857.png) |
(8.3) |
wobei 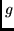 eine differenzierbare Funktion mit Wertebereich
eine differenzierbare Funktion mit Wertebereich
![$[0 \ldots 1]$](img858.png) ist.
ist.
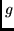 bestimmt, wie nahe eine Verbindungsadresse8.5den Aktivationen der Analyseknoten sein muß, um einen signifikanten
Beitrag für
bestimmt, wie nahe eine Verbindungsadresse8.5den Aktivationen der Analyseknoten sein muß, um einen signifikanten
Beitrag für 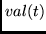 zu ermöglichen.
Ich schlage eine Funktion
zu ermöglichen.
Ich schlage eine Funktion 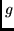 vor, die nahezu überall fast Null
ist, um den Ursprung herum jedoch eine enge Spitze
aufweist. Dies wird dem Netz im Prinzip
erlauben, sich zu jedem
Zeitpunkt eine einzelne Verbindung herauszupicken und ihr
gegenwärtiges Gewicht zu analysieren, ohne
`cross-talk' von anderen Gewichten in Kauf nehmen zu müssen.
vor, die nahezu überall fast Null
ist, um den Ursprung herum jedoch eine enge Spitze
aufweist. Dies wird dem Netz im Prinzip
erlauben, sich zu jedem
Zeitpunkt eine einzelne Verbindung herauszupicken und ihr
gegenwärtiges Gewicht zu analysieren, ohne
`cross-talk' von anderen Gewichten in Kauf nehmen zu müssen.
Es ist ohne weiteres möglich, alternative Schemata zur
gleichzeitigen Adressierung mehr als eines Gewichtes
zu entwerfen (siehe auch Fußnote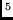 ).
).
4. Das Netz vermag all seine eigenen Gewichte zu modifizieren.
Eine Untermenge der Ausgabeknoten, welche weder
`normale' Ausgabeknoten noch Analyseknoten enthält, wird als
die Menge der
Modifizierknoten bezeichnet.
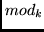 bezeichnet den
bezeichnet den 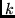 -ten von
-ten von 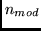 Modifizierknoten.
Die Modifizierknoten dienen dazu, sequentiell Verbindungen
anzusprechen, deren gegenwärtige Gewichte das Netzwerk `ändern
möchte'.
Es bereitet von neuem keine Schwierigkeiten, die
Modifizierknoten mit genügend Kapazität zur Adressierung
jeder beliebigen Verbindung auszustatten, einschließlich
jener Verbindungen, die zu Modifizierknoten führen.
Dies läßt sich wiederum durch
Modifizierknoten.
Die Modifizierknoten dienen dazu, sequentiell Verbindungen
anzusprechen, deren gegenwärtige Gewichte das Netzwerk `ändern
möchte'.
Es bereitet von neuem keine Schwierigkeiten, die
Modifizierknoten mit genügend Kapazität zur Adressierung
jeder beliebigen Verbindung auszustatten, einschließlich
jener Verbindungen, die zu Modifizierknoten führen.
Dies läßt sich wiederum durch
 |
(8.4) |
erreichen.
Ein spezieller Nichteingabeknoten, der weder
`normaler' Ausgabeknoten, Analyseknoten, noch Modifizierknoten ist,
wird mit
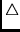 bezeichnet.
bezeichnet.
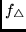 sollte sowohl positive als auch negative Aktivationen
sollte sowohl positive als auch negative Aktivationen
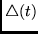 gestatten.
gestatten.
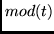 und
und
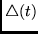 arbeiten zusammen, um explizite
Gewichtsänderungen gemäß
arbeiten zusammen, um explizite
Gewichtsänderungen gemäß
![\begin{displaymath}
w_{ij}(t+1) = w_{ij}(t) + \bigtriangleup(t)~g[~ \Vert adr(w_{ij}) - mod(t) \Vert^2~ ]
\end{displaymath}](img864.png) |
(8.5) |
hervorzurufen.
Ist 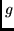 nahezu überall fast Null, weist aber
um den Ursprung herum eine enge Spitze
auf, so kann sich das Netz
zu jedem
Zeitpunkt eine einzelne Verbindung herauspicken und ihr
gegenwärtiges Gewicht ändern, ohne
andere Gewichte zu beeinflussen.
Es ist wiederum ohne weiteres möglich, alternative Schemata zur
gleichzeitigen Modifikation mehr als eines Gewichtes
zu entwerfen (siehe erneut Fußnote
nahezu überall fast Null, weist aber
um den Ursprung herum eine enge Spitze
auf, so kann sich das Netz
zu jedem
Zeitpunkt eine einzelne Verbindung herauspicken und ihr
gegenwärtiges Gewicht ändern, ohne
andere Gewichte zu beeinflussen.
Es ist wiederum ohne weiteres möglich, alternative Schemata zur
gleichzeitigen Modifikation mehr als eines Gewichtes
zu entwerfen (siehe erneut Fußnote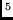 ).
).
Die Gleichungen (8.1), (8.3), und (8.5) beschreiben
im wesentlichen die vorverdrahtete Systemdynamik - die vom
Performanzmaß abhängigen Belegungen der Evalknoten
werden allerdings erst im Abschnitt 8.2 spezifiziert werden.
Abbildung:
Der spezielle Eingabevektor  informiert das
vollständig rückgekoppelte
Netzwerk (nur zwei Verbindungen sind eingezeichnet)
über externe Performanzevaluationen.
Der spezielle Ausgabevektor
informiert das
vollständig rückgekoppelte
Netzwerk (nur zwei Verbindungen sind eingezeichnet)
über externe Performanzevaluationen.
Der spezielle Ausgabevektor 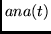 adressiert eine zu
analysierende Verbindung, deren Gewicht in den speziellen
Eingabeknoten
adressiert eine zu
analysierende Verbindung, deren Gewicht in den speziellen
Eingabeknoten 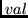 geschrieben wird.
Der spezielle Ausgabevektor
geschrieben wird.
Der spezielle Ausgabevektor 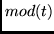 adressiert eine zu
modifizierende Verbindung, deren Gewicht in Proportion
zur gegenwärtigen Aktivation des
speziellen Ausgabeknotens
adressiert eine zu
modifizierende Verbindung, deren Gewicht in Proportion
zur gegenwärtigen Aktivation des
speziellen Ausgabeknotens
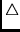 geändert wird.
Siehe Text für Details.
geändert wird.
Siehe Text für Details.
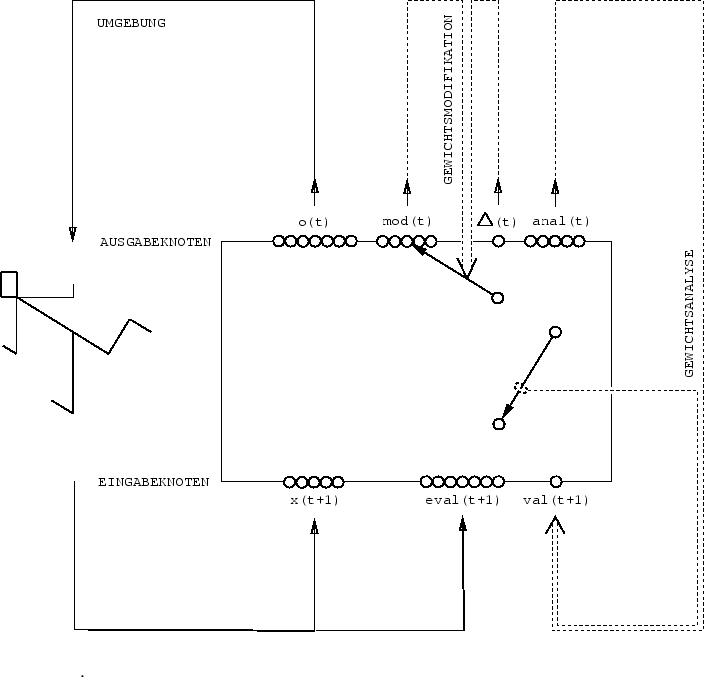 |
Tabelle 8.1:
Symboldefinitionen zur Beschreibung des `selbstreferentiellen' Netzes.
| Symbol |
Beschreibung |
|
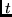 |
Diskreter Zeitindex aus
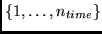 |
|
 |
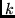 -ter `normaler' Eingabeknoten -ter `normaler' Eingabeknoten |
|
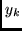 |
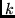 -ter Nichteingabeknoten -ter Nichteingabeknoten |
|
 |
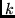 -ter `normaler' Ausgabeknoten -ter `normaler' Ausgabeknoten |
|
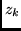 |
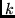 -ter Knoten -ter Knoten |
|
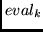 |
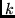 -ter Evalknoten (zur Beobachtung von Performanzevaluationen) -ter Evalknoten (zur Beobachtung von Performanzevaluationen) |
|
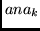 |
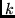 -ter Analyseknoten (um Verbindungen zu adressieren) -ter Analyseknoten (um Verbindungen zu adressieren) |
|
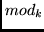 |
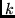 -ter Modifizierknoten (um Verbindungen zu adressieren) -ter Modifizierknoten (um Verbindungen zu adressieren) |
|
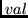 |
spezieller Eingabeknoten zur Analyse von Gewichten |
|
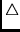 |
spezieller Ausgabeknoten, um Gewichte zu ändern |
|
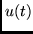 |
Aktivation von 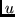 zur Zeit zur Zeit 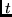 , falls , falls 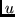 Knoten bezeichnet Knoten bezeichnet |
|
 |
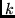 -te Komponente von -te Komponente von  , falls , falls  Vektor (konsistent mit
vorangegangener Zeile) Vektor (konsistent mit
vorangegangener Zeile) |
|
 |
`normaler' Eingabevektor zum Zeitpunkt 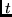 |
|
 |
`normaler' Ausgabevektor zum Zeitpunkt 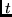 |
|
 |
Performanzevaluationsvektor zum Zeitpunkt 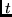 |
|
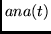 |
spezieller Ausgabevektor zur Adressierung von Verbindungen |
|
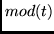 |
spezieller Ausgabevektor zur Adressierung von Verbindungen |
|
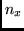 |
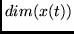 , Anzahl der normalen Eingabeknoten , Anzahl der normalen Eingabeknoten |
|
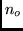 |
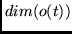 , Anzahl der `normalen' Ausgabeknoten , Anzahl der `normalen' Ausgabeknoten |
|
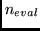 |
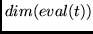 , Anzahl der Evalknoten , Anzahl der Evalknoten |
|
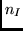 |
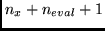 , Anzahl aller Eingabeknoten , Anzahl aller Eingabeknoten |
|
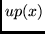 |
kleinste ganze Zahl 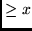 |
|
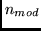 |
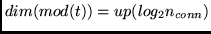 , Anzahl der Modifizierknoten , Anzahl der Modifizierknoten |
|
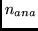 |
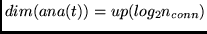 , Anzahl der Analysierknoten , Anzahl der Analysierknoten |
|
 |
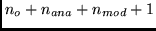 , Anzahl der Nichteingabeknoten , Anzahl der Nichteingabeknoten |
|
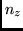 |
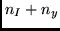 , Anzahl aller Knoten , Anzahl aller Knoten |
|
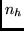 |
Anzahl der `versteckten' Knoten |
|
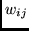 |
Verbindung vom Knoten 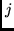 zum Knoten zum Knoten  |
|
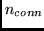 |
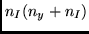 , Anzahl aller Verbindungen , Anzahl aller Verbindungen |
|
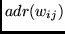 |
Adresse von 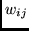 |
|
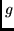 |
Funktion zur Definition der `Nähe' von Adressen, mit enger Spitze um
den Ursprung herum |
|
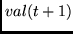 |
![$\sum_{i,j}g[ \Vert ana(t) - adr(w_{ij}) \Vert^2]w_{ij}(t)$](img880.png) |
|
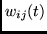 |
Gewicht von 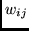 zum Zeitpunkt zum Zeitpunkt 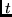 |
|
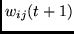 |
![$w_{ij}(t) + \bigtriangleup(t)~g[~ \Vert adr(w_{ij}) - mod(t) \Vert^2~ ]$](img882.png) |
|
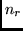 |
konstante Blockgröße,  bleibt während Blöcken der Länge bleibt während Blöcken der Länge 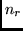 invariant invariant |
|
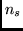 |
Anzahl sukzessiver Blöcke in der Eingabesequenz |
|
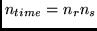 |
Anzahl sukzessiver Zeitschritte in der Eingabesequenz |
|
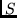 |
Menge der vom Netz ausführbaren Algorithmen |
|
|
Es gibt viele im obigen Sinne `selbstreferentielle' Netze. Der Begriff
`versteckte Knoten' bezeichne Knoten, die weder
`normale' Eingabeknoten,
`normale' Ausgabeknoten,
Evalknoten,
Analysierknoten,
Modifizierknoten,
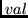 oder
oder
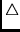 sind.
Es existieren
sind.
Es existieren 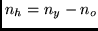 derartige versteckte Knoten.
Es gibt eine unendliche Anzahl von Möglichkeiten, die
Bedingung
derartige versteckte Knoten.
Es gibt eine unendliche Anzahl von Möglichkeiten, die
Bedingung
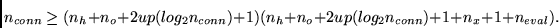 |
(8.6) |
zu erfüllen.
Ein Beispiel, bei dem das Gleichheitszeichen in (8.6) erfüllt ist,
ist durch
gegeben.




Nächste Seite: MÄCHTIGKEIT DER KLASSE DER
Aufwärts: EIN `SELBSTREFERENTIELLES' REKURRENTES NETZ
Vorherige Seite: `KONVENTIONELLE' ASPEKTE DER ARCHITEKTUR
Inhalt
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite
![]() )
bezeichnet.
)
bezeichnet.
![]() steht für den
steht für den ![]() -ten Evalknoten.
Obwohl
diese Modifikation konventioneller Netze
im Vergleich mit den folgenenden Modifikationen relativ
einfach ist, repräsentiert sie doch den möglicherweise
bedeutsamsten Beitrag zur Erzielung
`selbstreferentieller' Architekturen, wie Fußnote
-ten Evalknoten.
Obwohl
diese Modifikation konventioneller Netze
im Vergleich mit den folgenenden Modifikationen relativ
einfach ist, repräsentiert sie doch den möglicherweise
bedeutsamsten Beitrag zur Erzielung
`selbstreferentieller' Architekturen, wie Fußnote![]() , Abschnitt 8.1.3
noch etwas detaillierter ausführen wird.
, Abschnitt 8.1.3
noch etwas detaillierter ausführen wird.
![]() führen wir eine Adresse
führen wir eine Adresse
![]() ein.
Dies wird dem Netz helfen, über seine eigenen Verbindungen
zu `reden', wie die nächsten beiden Punkte klarmachen
werden.
O.B.d.A. nehmen wir im folgenden an, daß
ein.
Dies wird dem Netz helfen, über seine eigenen Verbindungen
zu `reden', wie die nächsten beiden Punkte klarmachen
werden.
O.B.d.A. nehmen wir im folgenden an, daß
![]() als Binärvektor repräsentiert sei (dies stellt jedoch
nur eine von vielen Möglichkeiten dar
als Binärvektor repräsentiert sei (dies stellt jedoch
nur eine von vielen Möglichkeiten dar![]() ).
).
![]() bezeichnet den
bezeichnet den ![]() -ten von
-ten von ![]() Analyseknoten.
Die Analyseknoten dienen dazu, sequentiell Verbindungen
anzusprechen, deren gegenwärtige Gewichte das Netzwerk `in Erfahrung
bringen möchte'.
Es bereitet keine Schwierigkeiten, die
Analyseknoten mit genügend Kapazität zur Adressierung
jeder beliebigen Verbindung auszustatten, einschließlich
jener Verbindungen, die zu Analyseknoten führen.
Dies läßt sich beispielsweise durch
Analyseknoten.
Die Analyseknoten dienen dazu, sequentiell Verbindungen
anzusprechen, deren gegenwärtige Gewichte das Netzwerk `in Erfahrung
bringen möchte'.
Es bereitet keine Schwierigkeiten, die
Analyseknoten mit genügend Kapazität zur Adressierung
jeder beliebigen Verbindung auszustatten, einschließlich
jener Verbindungen, die zu Analyseknoten führen.
Dies läßt sich beispielsweise durch
![]() ).
).
![]() bezeichnet den
bezeichnet den ![]() -ten von
-ten von ![]() Modifizierknoten.
Die Modifizierknoten dienen dazu, sequentiell Verbindungen
anzusprechen, deren gegenwärtige Gewichte das Netzwerk `ändern
möchte'.
Es bereitet von neuem keine Schwierigkeiten, die
Modifizierknoten mit genügend Kapazität zur Adressierung
jeder beliebigen Verbindung auszustatten, einschließlich
jener Verbindungen, die zu Modifizierknoten führen.
Dies läßt sich wiederum durch
Modifizierknoten.
Die Modifizierknoten dienen dazu, sequentiell Verbindungen
anzusprechen, deren gegenwärtige Gewichte das Netzwerk `ändern
möchte'.
Es bereitet von neuem keine Schwierigkeiten, die
Modifizierknoten mit genügend Kapazität zur Adressierung
jeder beliebigen Verbindung auszustatten, einschließlich
jener Verbindungen, die zu Modifizierknoten führen.
Dies läßt sich wiederum durch

![]() oder
oder
![]() sind.
Es existieren
sind.
Es existieren ![]() derartige versteckte Knoten.
Es gibt eine unendliche Anzahl von Möglichkeiten, die
Bedingung
derartige versteckte Knoten.
Es gibt eine unendliche Anzahl von Möglichkeiten, die
Bedingung