ARCHITEKTUR UND AKTIVIERUNGSDYNAMIK

Zu unseren Netzwerken gehören Eingabeknoten und `interne' Knoten (auch Nichteingabeknoten genannt). Wie im folgenden zu sehen sein wird, werden Eingabeknoten von Eingabemustern aus der Umgebung aktiviert, während interne Knoten ihre Aktivationen gemäß einfacher Regeln aus den Aktivationen der übrigen Knoten berechnen. Die Bezeichnung `vollständige Rückkopplung' soll besagen, daß jeder Eingabeknoten genau eine gerichtete Verbindung zu jedem internen Knoten aufweist, und daß jedem internen Knoten ebenfalls genau eine gerichtete Verbindung zu jedem internen Knoten (einschließlich sich selbst, siehe Abbildung 2.1) entspringt.

Abbildung: Ein rekurrentes Netz mit 3 Eingabeknoten (weiße Kreise) und 5 vollständig miteinander vernetzten internen Knoten (grau). 2 der internen Knoten dienen gleichzeitig als Ausgabeknoten. Das Gewicht der gerichteten Verbindung vom $j$-ten Knoten zum $i$-ten Knoten besitzt den Wert $w_{ij}$.

Bei der Wahl formaler Symbole halten wir uns relativ eng an die Notation von Williams und Peng [149]. Um Indizes zu sparen, betrachten wir der Einfachheit halber eine einzelne, $s$ diskrete Zeitschritte umfassende geordnete Sequenz von vektorwertigen Eingabemustern. Zu jedem Zeitpunkt $0 < t \leq s$ ist der reellwertige Vektor der Aktivationen der Eingabeknoten gleich dem $t$-ten Eingabemuster. Alle Knoten seien in beliebiger Weise eindeutig durchnumeriert. $U$ bezeichne die Menge von Indizes $k$ mit der Eigenschaft, daß $x_k(t)$ die Ausgabe des internen Knotens mit der Nummer $k$ zum Zeitpunkt $t$ ist. $I$ stehe für die Menge von Indizes $k$ mit der Eigenschaft, daß $x_k(t)$ die Eingabe des Eingabeknotens mit der Nummer $k$ zum Zeitpunkt $t$ darstellt. Es sei

$$\mid I \mid = m, \mid U \mid = n, m = O(n).$$

Das reellwertige skalare Gewicht der gerichteten Verbindung vom Knoten $j$ zum Knoten $i$ wird durch $w_{ij}$ denotiert. Während der Verarbeitung der Eingabesequenz ändern sich die Gewichte nicht. Um jedoch zwischen verschiedenen Instanzen von $w_{ij}$ zu verschiedenen Zeitpunkten unterscheiden zu können, verwenden wir die Notation $w_{ij}(t)$ für das Gewicht der Verbindung vom Knoten $j$ zum Knoten $i$ zum Zeitpunkt $t$. Dies hat rein formale Gründe: $\forall t:~~ w_{ij}(t) = w_{ij}$.

Die Ablaufdynamik definieren wir für $k \in U$ wie folgt:

$$net_k(0)=0, ~~\forall t \geq 0: x_k(t) = f_k(net_k(t)),$$

$$~~\forall t>0:~~ net_k(t+1) = \sum_{l \in U \cup I} w_{kl}(t+1)x_l(t),$$ (2.1)

wobei $f_k$ eine differenzierbare (gewöhnlich streng monoton wachsende) Aktivierungsfunktion bezeichnet, häufig die logistische Funktion

$$f(x) = \frac{1}{1 + e^{-x}}.$$ (2.2)

Letztere läßt sich einfach ableiten:

$$f'(x) = f(x)(1 - f(x)).$$ (2.3)

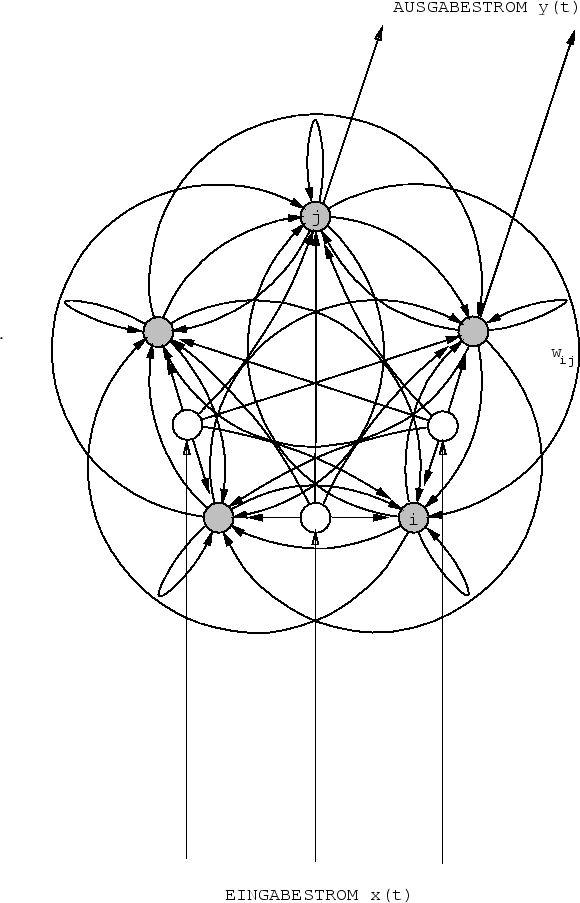
Turingäquivalenz. Obige zyklische Verbindungsstruktur weist zwar Ähnlichkeiten zur Topologie von Hopfieldnetzen [38], Boltzmannmaschinen [36], Schürmann-Netzen [123], und BP-Equilibriumsnetzen ([2], [81], [70], [71]) auf. Diese Ansätze sind allerdings nur für stationären Eingaben gedacht und für das Erlernen von Sequenzen ungeeignet - die Rekurrenz im Netz dient bei obigen Referenzen lediglich zur Ermittlung eines Aktivationsequilibriums. Die Aktivierungsdynamik (2.1) hingegen erlaubt zeitlich veränderliche Eingaben. Dieser wesentliche Unterschied bildet die Grundlage für ein System, das im Prinzip die Mächtigkeit einer Turingmaschine besitzt - und zwar im selben Sinne, in dem jeder konventionelle Rechner einer Turingmaschine gleichkommt. Dies ist unschwer einzusehen: Mit entsprechenden Gewichten kann man in einem hinreichend großen Netzwerk jede Boolesche Funktion und damit auch jede Kombination Boolescher Funktionen verdrahten. Damit läßt sich bei geeigneter Gewichtsbelegung die sequentielle Arbeitsweise eines herkömmlichen seriell arbeitenden Digitalrechners exakt emulieren - das einzige Hemmnis auf dem Weg zur `wahren' Turingäquivalenz ist, wie stets, der endliche Speicherplatz.

Natürlich hat dieses Argument nur theoretische Bedeutung: Niemand wollte ernsthaft mittels eines zyklischen Netzes einen gewöhnlichen Digitalrechner nachbauen^2.1. Vorteile erhofft man sich ja gerade von der Möglichkeit zumindest teilweise paralleler Informationsverarbeitung. Um unter den vielen Programmen, die ein zyklisches neuronales Netz ausführen könnte, bestimmte zweckmäßige Programme (= Gewichtsbelegungen) auszuzeichnen, definieren wir nun ein geeignetes

Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite