Dieser Abschnitt präsentiert den
ersten originären Beitrag der vorliegenden Arbeit.
Wie oben gesehen, beträgt RTRLs
Berechnungskomplexität2.2pro Zeitschritt ![]() .
Im folgenden werden wir die Gradientenkalkulation
so umarrangieren, daß die Speicherkomplexität des
neuen Verfahrens dieselbe
Ordnung wie die von RTRL aufweist, die Berechnungskomplexität
aber in Proportion zur Zahl der Knoten im Netzwerk sinkt.
Im Gegensatz zu der in [156] vorgestellten ad-hoc
Methode bestimmt das neuartige Verfahren den exakten Gradienten,
nicht etwa nur eine Approximation desselben [109].
.
Im folgenden werden wir die Gradientenkalkulation
so umarrangieren, daß die Speicherkomplexität des
neuen Verfahrens dieselbe
Ordnung wie die von RTRL aufweist, die Berechnungskomplexität
aber in Proportion zur Zahl der Knoten im Netzwerk sinkt.
Im Gegensatz zu der in [156] vorgestellten ad-hoc
Methode bestimmt das neuartige Verfahren den exakten Gradienten,
nicht etwa nur eine Approximation desselben [109].
Alle ![]() Zeitschritte benötigt die neue Methode
Zeitschritte benötigt die neue Methode
![]() Operationen, bei allen dazwischenliegenden Zeitschritten sind
allerdings nur
Operationen, bei allen dazwischenliegenden Zeitschritten sind
allerdings nur
![]() Operationen erforderlich. Dies drückt die durchschnittliche
Zeitkomplexität pro Zeitschritt auf
Operationen erforderlich. Dies drückt die durchschnittliche
Zeitkomplexität pro Zeitschritt auf
![]() .
.
Eine Trainingssequenz mit ![]() Zeitschritten startet wieder
zum Zeitschritt 0 und endet zum Zeitschritt
Zeitschritten startet wieder
zum Zeitschritt 0 und endet zum Zeitschritt ![]() . Der nachfolgende
Algorithmus ist von Interesse, falls
. Der nachfolgende
Algorithmus ist von Interesse, falls
![]() (sonst sei BPTT empfohlen).
(sonst sei BPTT empfohlen).
Der Algorithmus2.3 ist ein Hybrid zwischen BPTT und RTRL [109].
Die folgende Beschreibung enthält sowohl die Herleitung
als auch einige Kommentare zur Komplexität der einzelnen Schritte.
Die wesentliche Idee ist: Zerlege die Gradientenberechnung in
mehrerere Blöcke, von denen jeder ![]() Zeitschritte
umfaßt. Führe für jeden Block
Zeitschritte
umfaßt. Führe für jeden Block ![]() BPTT-ähnliche
Berechnungsphasen durch. Eine davon dient zur Bestimmung
gewisser Fehlergradienten, die restlichen
BPTT-ähnliche
Berechnungsphasen durch. Eine davon dient zur Bestimmung
gewisser Fehlergradienten, die restlichen ![]() Phasen dienen zur
Berechnung der partiellen Ableitungen der Netzeingaben
jedes internen Knotens am Ende jedes Blocks. Führe schließlich
Phasen dienen zur
Berechnung der partiellen Ableitungen der Netzeingaben
jedes internen Knotens am Ende jedes Blocks. Führe schließlich
![]() RTRL-ähnliche Berechnungsphasen durch, um die Resultate
der BPTT-Phasen mit den aus früher abgearbeiteten Blocks
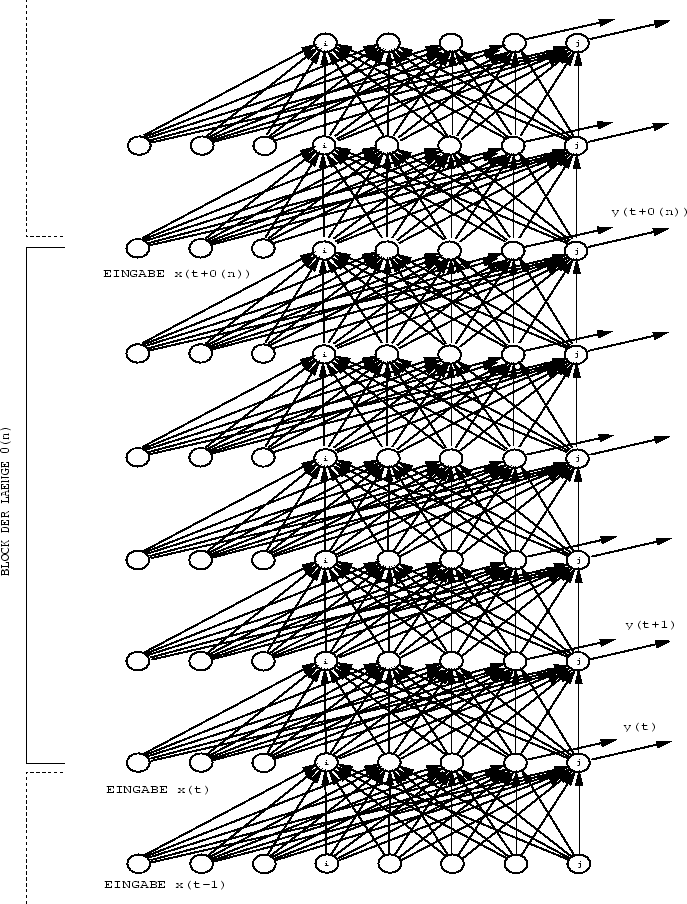
gewonnenen Resultaten zu verrechnen. Siehe Abbildung 2.3.
RTRL-ähnliche Berechnungsphasen durch, um die Resultate
der BPTT-Phasen mit den aus früher abgearbeiteten Blocks
gewonnenen Resultaten zu verrechnen. Siehe Abbildung 2.3.
 |
Für alle ![]() und für alle
und für alle
![]() definieren wir
definieren wir
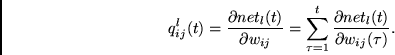
Zu Beginn des Algorithmus setzen wir die Variable
![]() .
.
![]() bezeichnet den ersten Zeitschritt des gegenwärtigen Blocks.
Man beachte, daß
für alle in Frage kommenden
bezeichnet den ersten Zeitschritt des gegenwärtigen Blocks.
Man beachte, daß
für alle in Frage kommenden ![]() gilt:
gilt:
Die Hauptschleife des Algorithmus umfaßt 5 Schritte.
1. SCHRITT: Setze
![]() (es sei empfohlen:
(es sei empfohlen:
![]() ).
).
Die Größe
![]() ist für alle
ist für alle
![]() bereits bekannt. Dasselbe gilt für
bereits bekannt. Dasselbe gilt für
![]() für alle in Frage kommenden
für alle in Frage kommenden ![]() .
Gesucht ist eine effiziente Methode zur Bestimmung des Beitrags von
.
Gesucht ist eine effiziente Methode zur Bestimmung des Beitrags von
![]() zur Änderung von
zur Änderung von ![]() ,
,
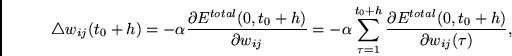
2. SCHRITT: Führe eine Aktivationsausbreitungsphase
für die Zeitschritte ![]() bis einschließlich
bis einschließlich ![]() gemäß der in Gleichung (2.1) spezifizierten
Aktivierungsdynamik durch. Stellt sich zur Laufzeit heraus, daß
die gegenwärtige Trainingssequenz weniger als
gemäß der in Gleichung (2.1) spezifizierten
Aktivierungsdynamik durch. Stellt sich zur Laufzeit heraus, daß
die gegenwärtige Trainingssequenz weniger als
![]() Zeitschritte umfaßt
(i.e.,
Zeitschritte umfaßt
(i.e., ![]() ), dann setze
), dann setze
![]() . Falls
. Falls
![]() , terminiere den Algorithmus.
, terminiere den Algorithmus.
3. SCHRITT:
Führe zur Berechnung von Fehlerableitungen
folgende Kombination einer BPTT-ähnlichen Berechnungsphase
mit einer RTRL-ähnlichen Berechnungsphase
durch. Wir schreiben
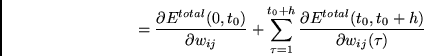
 |
(2.7) |
Wir kennen bereits den ersten Term des Ausdrucks (2.7). Man konzentriere sich auf den dritten Term:

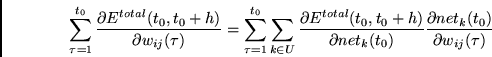

4. SCHRITT:
Um
![]() für alle möglichen
für alle möglichen ![]() zu berechnen, führe
zu berechnen, führe
![]() BPTT/RTRL-Kombinationen
(eine solche Kombination für jedes
BPTT/RTRL-Kombinationen
(eine solche Kombination für jedes ![]() ) aus:
) aus:
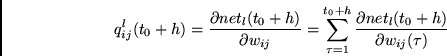
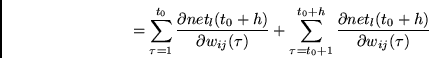
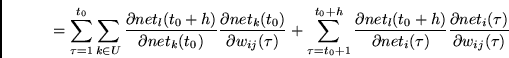
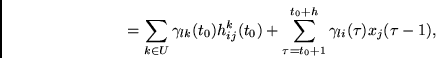 |
(2.8) |
Für gegebenes ![]() kostet die Berechnung von (2.8)
für alle
kostet die Berechnung von (2.8)
für alle ![]()
![]() Operationen.
Der 3. und der 4. SCHRITT
brauchen zusammen also
Operationen.
Der 3. und der 4. SCHRITT
brauchen zusammen also
![]() Operationen,
die sich allerdings über
Operationen,
die sich allerdings über ![]() Zeitschritte verteilen.
Da wir zu Beginn
Zeitschritte verteilen.
Da wir zu Beginn ![]() gesetzt haben, verstreuen sich
demzufolge
gesetzt haben, verstreuen sich
demzufolge
![]() Operationen über
Operationen über ![]() Zeitschritte.
Dies zieht eine durchschnittliche Berechnungskomplexität
der Ordnung
Zeitschritte.
Dies zieht eine durchschnittliche Berechnungskomplexität
der Ordnung ![]() nach sich.
nach sich.
Der 5. Schritt schließt die Hauptschleife des Algorithmus ab:
5. SCHRITT: Setze
![]() und springe zum 1. SCHRITT.
und springe zum 1. SCHRITT.
So wie er oben formuliert wurde, führt der Algorithmus
bei jedem ![]() -ten Zeitschritt zu
einen Spitzenberechnungsaufwand von
-ten Zeitschritt zu
einen Spitzenberechnungsaufwand von
![]() Operationen.
Nichts hält uns jedoch davon ab,
diese
Operationen.
Nichts hält uns jedoch davon ab,
diese ![]() Berechnungen gleichmäßig über
Berechnungen gleichmäßig über
![]() Zeitschritte zu verteilen. Man könnte zum Beispiel
zu jedem Zeitschritt des
Zeitschritte zu verteilen. Man könnte zum Beispiel
zu jedem Zeitschritt des ![]() -ten Blocks eine der
-ten Blocks eine der
![]() BPTT-Phasen des 4. SCHRITTs des
BPTT-Phasen des 4. SCHRITTs des ![]() -ten Blocks
durchführen. Dies würde auch den Spitzenberechnungsaufwand pro
Zeitschritt auf
-ten Blocks
durchführen. Dies würde auch den Spitzenberechnungsaufwand pro
Zeitschritt auf ![]() drücken.
drücken.
Die off-line Version des Algorithmus führt die Gesamtgewichtsänderung nach Abschluß der Präsentation aller Trainingssequenzen aus.
Die korrespondierende on-line-Version
ändert die Gewichte jeweils nach dem 4. SCHRITT (also jeweils
nach der Abarbeitung eines Blockes der Zeitdauer ![]() ).
Die im nächsten Abschnitt (sowie in den Arbeiten der
anderen in diesem Kapitel aufgeführten Autoren)
beschriebenen Experimente verwenden für alle
Versionen aller drei oben betrachteten Algorithmen
gewöhnlich Lernraten zwischen 0.01 und 1.0.
).
Die im nächsten Abschnitt (sowie in den Arbeiten der
anderen in diesem Kapitel aufgeführten Autoren)
beschriebenen Experimente verwenden für alle
Versionen aller drei oben betrachteten Algorithmen
gewöhnlich Lernraten zwischen 0.01 und 1.0.