REKURSIVE AUTO-ASSOZIATIVE GEDÄCHTNISSE

Ein noch zu spezifizierender `Autoassoziator' $A$ wird daraufhin trainiert, jede Eingabesequenz sowie all ihre Anfangssequenzen in eindeutiger Weise zu repräsentieren (dies ist eine Form der Quellenkodierung). Ein zusätzliches überwacht lernendes azyklisches Netzwerk erhält $A$'s eindeutige Repräsentationen als Eingabe und lernt, ein durch allgemeine Fehlertrajektorien definiertes Performanzmaß zu minimieren^7.6.

Wir fokussieren uns hier auf den Autoassoziator $A$. $A$'s einziges Ziel besteht in der Kreierung unterschiedlicher interner Zustandsvektoren in Antwort auf unterschiedliche Eingabesequenzen.

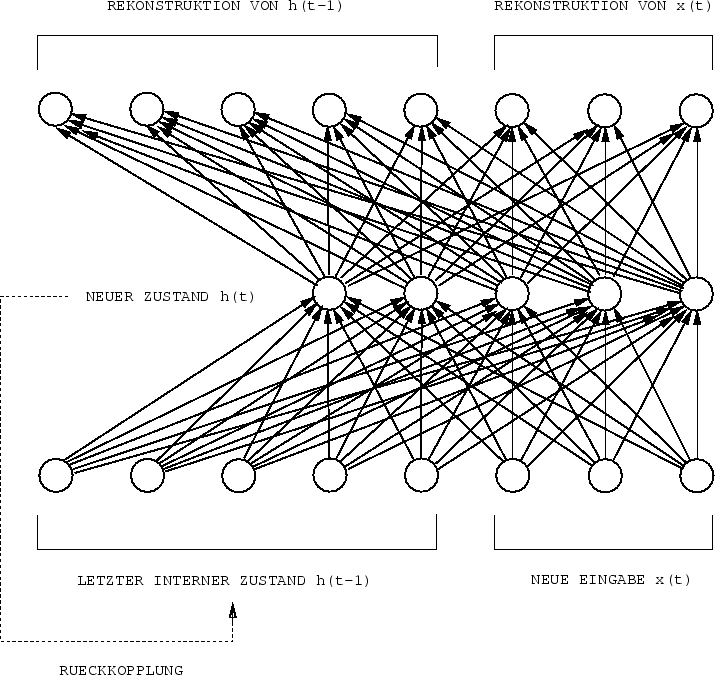
Architektur und Zielfunktion. Es gibt drei Klassen von Knoten: Eingabeknoten, `versteckte' Knoten, und Ausgabeknoten. Alle Eingabeknoten von $A$ sind mit allen versteckten Knoten verbunden. Alle versteckten Knoten weisen Verbindungen zu allen Ausgabeknoten auf. $A$'s interner Zustandsvektor $h^p(t)$ ist der Aktivationsvektor seiner versteckten Knoten zum Zeitpunkt $t$ der sich über $n_p$ Zeitschritte erstreckenden Sequenz $p$. $A$'s Eingabe zur Zeit $t > 1$ ist $h^p(t-1) \circ x^p(t)$. Für alle $p$ nimmt der interne Initialzustand $h^p(0)$ zum Zeitpunkt 0 einen `Defaultwert' an, z.B. den Nullvektor. Zur Zeit $0<t \leq n_p$, berechnet $A$

$$h^p(t) = g ( x^p(t), h^p(t-1)),$$

wobei $g$ durch die konventionellen Aktivationsausbreitungsregeln für BP-Netze definiert ist (siehe Kapitel 1). $A$'s Ausgabevektor $z^p(t)$ wird aus $h^p(t)$ ebenfalls gemäß der BP-Aktivationsausbreitungsregeln bestimmt. Die Anzahl von $A$'s Ausgabeknoten ergibt sich zur Summe der Anzahlen seiner Eingabeknoten und versteckten Knoten. $z^p(t)$ wird nun als `Rekonstruktion' von $x^p(t) \circ h^p(t-1)$ interpretiert. Siehe Abbildung 2.5.

Abbildung: Ein rekursives auto-assoziatives Gedächtnis assoziiert die Kombination des letzten internen Zustands und der neuen Eingabe mit sich selbst - dadurch wird eine Beschreibung der bisher beobachteten Eingabesequenz in den neuen internen Zustand `hineinkomprimiert'.

Durch konventionelles BP wird $g$ so modifiziert, daß die $h^p(t), 0<t<n_p$ Werte annehmen, die es erlauben, $h^p(t-1)$ und $x^p(t)$ zu rekonstruieren. $A$'s Zielfunktion zur Zeit $t$ der Sequenz $p$ ist dabei

$$E_A(t) = \frac{1}{2} \left[ x^p(t) \circ h^p(t-1) - z^p(t)\right]^T \left[x^p(t) \circ h^p(t-1) - z^p(t)\right].$$

Zur Minimierung von $E_A(t)$ wird nicht etwa wie bei BPTT bis zum Beginn der gegenwärtig behandelten Sequenz zurückpropagiert, sondern lediglich bis zu $h^p(t-1)$. Damit bekommen wir zwar keinen exakten Gradientenabstieg in $E_A = \sum E_A(t)$, wohl aber einen Algorithmus, (im wesentlichen den von Pollack vorgeschlagenen^7.7), dessen Berechnungskomplexität pro Verbindung und Zeitschritt unabhängig von der Netzgröße konstant ist. Warum sollte dieser Algorithmus $A$ dazu zwingen, eindeutige interne Zustände für theoretisch beliebig lange Sequenzen und all ihre Subsequenzen zu generieren?

Die Antwort läßt sich leider nur informell durch Induktion über die Länge der längsten Trainingssequenz sehen (hier haben wir ein Beispiel für einen Lernalgorithmus, der nicht allein aus der Kettenregel gerechtfertigt werden kann):

1. Nehmen wir an, es gibt $s$ verschiedene Trainingssequenzen $1, \ldots, s$. Die Länge der Sequenz $p$ beträgt $n_p>0$. Für alle $p = 1, \ldots, s$ wird $h^p(1)$ daraufhin trainiert, die Rekonstruktion von $h^p(0)$ und $x^p(1)$ zu ermöglichen. Demzufolge werden die Anfänge aller Sequenzen eindeutig in $h$ repräsentiert sein.

2. Setzen wir nun voraus, daß alle Sequenzen und Subsequenzen der Länge $<k$ bereits eindeutige Repräsentationen in $h$ verursachen. Für alle Sequenzen und Subsequenzen $p$ mit Länge $k$ zwingen wir $h^p(k)$, die Rekonstruktion von $h^p(k-1)$ and $x^p(k)$ zu ermöglichen. Damit werden alle Sequenzen und Subsequenzen mit Länge $<k+1$ eindeutige Repräsentationen in $h$ nach sich ziehen. $\Box$

Obiges Argument vernachlässigt allerdings ein Potential für sogenannten `crosstalk', z.B. die durch den zweiten Schritt eröffnete Möglichkeit, daß Sequenzen der Länge $<k$ durch Eintrainieren der Sequenzen der Länge $k$ wieder `vergessen' werden. In Experimenten zeigt sich jedoch, daß RAAMs zur Sequenzcodierung durchaus geeignet sind.

Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite