![]() bezeichnet das
Prediktornetzwerk der
bezeichnet das
Prediktornetzwerk der ![]() -ten Ebene. Zur Implementierung von
-ten Ebene. Zur Implementierung von ![]() eignen sich im Prinzip beliebige rekurrente Netze für dynamische Umgebungen
(e.g
[40], [23], [14], [74],
[85], [144], [149],
[59], [79], [3], [150], [148], [152], [109], [112], [29], [68], [72], [28], [147], [90], [97]7.3).
Zu jedem Zeitpunkt einer Sequenz
eignen sich im Prinzip beliebige rekurrente Netze für dynamische Umgebungen
(e.g
[40], [23], [14], [74],
[85], [144], [149],
[59], [79], [3], [150], [148], [152], [109], [112], [29], [68], [72], [28], [147], [90], [97]7.3).
Zu jedem Zeitpunkt einer Sequenz ![]() besteht die Eingabe für die
unterste Ebene aus
besteht die Eingabe für die
unterste Ebene aus ![]() .
Wir nehmen an, daß die Umgebung
folgender (in allen vernünftigen Fällen erfüllten) Bedingung
Genüge leistet:
.
Wir nehmen an, daß die Umgebung
folgender (in allen vernünftigen Fällen erfüllten) Bedingung
Genüge leistet:
Bedingung 7.3:
Zu jeder reellwertigen Prediktion
eines Eingabevektors läßt sich
unter allen möglichen Eingabevektoren
einer angeben, dessen euklidischer Abstand zur
Prediktion
minimal ist.
Wann immer ein ![]() daran scheitert, seine eigene nächste
Eingabe vorherzusagen (u.a. auch nach einem `nullten'
Initialisierungszeitschritt zu Beginn jeder Sequenz),
ergibt sich
daran scheitert, seine eigene nächste
Eingabe vorherzusagen (u.a. auch nach einem `nullten'
Initialisierungszeitschritt zu Beginn jeder Sequenz),
ergibt sich ![]() 's Eingabe
durch die Konkatenation der tatsächlich beobachteten Eingabe
und einer eindeutigen Repräsentation des entsprechenden
Zeitschritts7.4.
Die Aktivationen von
's Eingabe
durch die Konkatenation der tatsächlich beobachteten Eingabe
und einer eindeutigen Repräsentation des entsprechenden
Zeitschritts7.4.
Die Aktivationen von ![]() 's versteckten Knoten
und Ausgabeknoten werden nur zu den `kritischen'
Zeitpunkten der nächstniedrigeren Ebene aktualisiert.
Diese Prozedur stellt sicher, daß
's versteckten Knoten
und Ausgabeknoten werden nur zu den `kritischen'
Zeitpunkten der nächstniedrigeren Ebene aktualisiert.
Diese Prozedur stellt sicher, daß
![]() ohne Informationsverlust mit einer eindeutigen
reduzierten Beschreibung der Sequenz
ohne Informationsverlust mit einer eindeutigen
reduzierten Beschreibung der Sequenz ![]() gefüttert wird7.5.
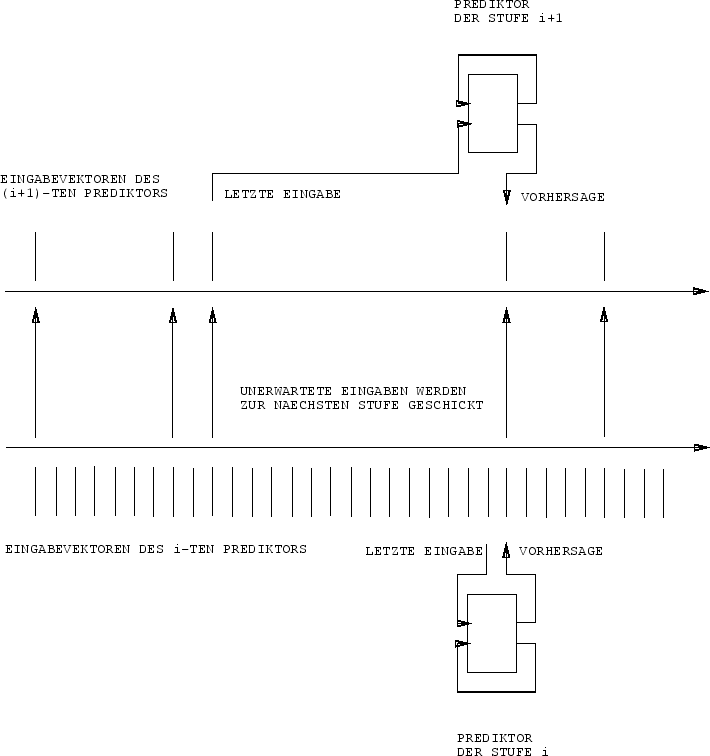
Das Prinzip der
Geschichtskompression
liefert
hierfür
die theoretische Grundlage. Siehe Abbildung 7.1.
gefüttert wird7.5.
Das Prinzip der
Geschichtskompression
liefert
hierfür
die theoretische Grundlage. Siehe Abbildung 7.1.
 |
Im allgemeinen wird
![]() weniger Eingaben pro Zeiteinheit erhalten als
weniger Eingaben pro Zeiteinheit erhalten als ![]() .
Nach Sektion 7.1 sollte
.
Nach Sektion 7.1 sollte
![]() damit i.a.
weniger Schwierigkeiten als
damit i.a.
weniger Schwierigkeiten als ![]() haben, zu lernen,
haben, zu lernen,
![]() 's `kritische Eingaben' vorherzusagen. Dies darf man
aber nur dann erwarten,
wenn der Eingabestrom globale zeitliche Regularitäten
enthält, die
's `kritische Eingaben' vorherzusagen. Dies darf man
aber nur dann erwarten,
wenn der Eingabestrom globale zeitliche Regularitäten
enthält, die ![]() noch nicht entdeckt hat.
In Umgebungen ohne hierarchische zeitlichen Strukturen
bietet das Multiebenensystem keine Vorteile. Typische
Eingabeströme scheinen allerdings hierarchisch
aufgebaut zu sein - man denke nur an Sprachsignale.
(Siehe [77] für einen verwandten ad-hoc Ansatz
zur Lösung von Aufgaben aus dem Bereich R-Lernen.)
noch nicht entdeckt hat.
In Umgebungen ohne hierarchische zeitlichen Strukturen
bietet das Multiebenensystem keine Vorteile. Typische
Eingabeströme scheinen allerdings hierarchisch
aufgebaut zu sein - man denke nur an Sprachsignale.
(Siehe [77] für einen verwandten ad-hoc Ansatz
zur Lösung von Aufgaben aus dem Bereich R-Lernen.)