Wie bereits erwähnt, wird
![]() i. a. auf einer `langsameren' Zeitskala als
i. a. auf einer `langsameren' Zeitskala als ![]() arbeiten;
die Zeitskala der Ebene
arbeiten;
die Zeitskala der Ebene ![]() wird durch die von
wird durch die von
![]() nicht korrekt vorhergesagten Eingaben definiert.
Der
nicht korrekt vorhergesagten Eingaben definiert.
Der ![]() -te Zeitschritt der zur
-te Zeitschritt der zur
![]() -ten Ebene gehörigen Zeitskala sei mit
-ten Ebene gehörigen Zeitskala sei mit ![]() oder
auch mit
oder
auch mit ![]() bezeichnet.
bezeichnet.
![]() aktualisiert die Aktivationen seiner Knoten
ausschließlich zu den Zeitpunkten
aktualisiert die Aktivationen seiner Knoten
ausschließlich zu den Zeitpunkten
![]() .
Bei gegebener
Sequenz
.
Bei gegebener
Sequenz ![]() stehe
stehe ![]() für
für
![]() 's
Eingabevektor zum Zeitpunkt
's
Eingabevektor zum Zeitpunkt ![]() .
Der Ausgabevektor trage den Namen
.
Der Ausgabevektor trage den Namen ![]() .
Wir nehmen an, daß
Bedingung 7.3 erfüllt ist.
Als aktuelle Vorhersage
.
Wir nehmen an, daß
Bedingung 7.3 erfüllt ist.
Als aktuelle Vorhersage
![]() wird derjenige der möglichen Eingabevektoren angesehen, der
den geringsten euklidischen Abstand zu
wird derjenige der möglichen Eingabevektoren angesehen, der
den geringsten euklidischen Abstand zu ![]() aufweist
(siehe Bedingung 7.3).
Gibt es mehrere derartige Eingabevektoren, so wird derjenige
mit der kleinsten Nummer (bei beliebiger Ordnung auf der
Menge der möglichen Eingabevektoren) herausgepickt. So
erhalten wir eine eindeutige deterministische Vorhersage.
Wir gehen inkrementell vor: Zunächst wird
aufweist
(siehe Bedingung 7.3).
Gibt es mehrere derartige Eingabevektoren, so wird derjenige
mit der kleinsten Nummer (bei beliebiger Ordnung auf der
Menge der möglichen Eingabevektoren) herausgepickt. So
erhalten wir eine eindeutige deterministische Vorhersage.
Wir gehen inkrementell vor: Zunächst wird
![]() trainiert, nach
trainiert, nach ![]() 's Trainingsphase werden alle Gewichte
in
's Trainingsphase werden alle Gewichte
in ![]() `eingefroren' und
`eingefroren' und ![]() 's Trainingsphase beginnt, etc.
's Trainingsphase beginnt, etc.
![]() 's Zielfunktion ist gleich
's Zielfunktion ist gleich
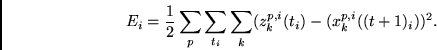 |
(7.4) |
Ist ![]() (höhere Level), so gilt
(höhere Level), so gilt
Falls die Menge der potentiellen Eingabevektoren
überabzählbar unendlich viele Elemente enthält (z. B. alle
möglichen reellen Vektoren mit der Dimension des Eingaberaums), so
macht es Sinn, sich ein `Epsilon' ![]() definieren, welches
`akzeptable Vorhersagefehler' definiert:
Gilt
definieren, welches
`akzeptable Vorhersagefehler' definiert:
Gilt