---

Metalearning Machines Learn to Learn (1987-)

---

Abstract. In 2020 we celebrated the 1/3 century anniversary of my first publication on metalearning or learning to learn: my diploma thesis of 1987 [META1] (Sec. 1). For its cover I drew a robot that bootstraps itself (image above). [META1] was the first in a long series of publications on this topic, which became hot in the 2010s [DEC]. Here I also summarize our work on meta-reinforcement learning with self-modifying policies since 1994 [METARL2-9] (Sec. 2), gradient descent-based metalearning in artificial neural networks since 1992 [FWPMETA1-5] (Sec. 3), asymptotically optimal metalearning for curriculum learning since 2002 [OOPS1-3] (Sec. 4), mathematically optimal metalearning through the self-referential Gödel Machine since 2003 [GM3-9] (Sec. 5), Meta-RL combined with artificial curiosity and intrinsic motivation [AC] since 1990/1997 (Sec. 6), and recent work of 2020-2022 (Sec. 7). See also this YouTube video on metalearning.

The most widely used machine learning algorithms were invented and hardwired by humans. Can we also construct metalearning (or meta-learning) algorithms that can learn better learning algorithms, to build truly self-improving AIs without any limits other than the limits of computability and physics? This question has been a main drive of my research since my 1987 diploma thesis on this topic [META1].

First note that metalearning is sometimes confused with simple transfer learning from one training set to another (see N(eur)IPS 2016 slides). However, even a standard deep feedforward neural network (NN) can transfer-learn to learn new images faster through pre-training on other image sets, e.g., [TRA12]. True metalearning is much more than that, and also much more than just learning to adjust hyper-parameters such as mutation rates in evolution strategies.

True metalearning is about encoding the initial learning algorithm in a universal programming language (e.g., on a recurrent neural network or RNN), with primitive instructions that allow for modifying the code itself in arbitrary computable fashion. We surround this self-referential, self-modifying code by a recursive framework that ensures that only "useful" self-modifications survive, to allow for Recursive Self-Improvement (RSI), e.g., Sec. 2, Sec. 5.

Metalearning may be the most ambitious but also the most rewarding goal of machine learning. There are few limits to what a good metalearner will learn. Where appropriate, it will learn to learn by analogy, by chunking, by planning, by subgoal generation, by combinations thereof—you name it.

---

1. Meta-Evolution and PSALMs (1987)

---

In 1987, we published [GP87] [GP] what I think was the first paper on Genetic Programming or GP for evolving programs of unlimited size written in a universal programming language [GOD][GOD34][CHU][TUR][POS].

In the same year, Sec. 2 of my diploma thesis [META1] applied such GP to itself, to recursively evolve better GP methods. There was not only a meta-level but also a meta-meta-level and a meta-meta-meta-level etc. I called this Meta-Evolution.

Sec. 4 of [META1] also introduced metalearning Prototypical Self-Referential Associating Learning Mechanisms (PSALMs) for payoff maximisation or Reinforcement Learning (RL). This was a first kind of meta-RL.

---

2. Meta-Reinforcement Learning with Self-Modifying Policies (1994-)

---

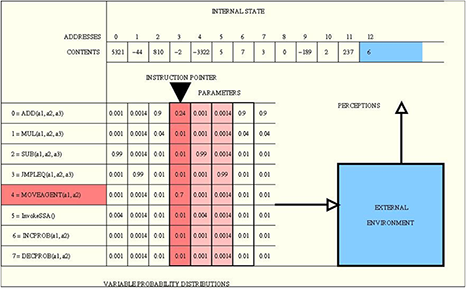In 1994, I proposed another type of meta-RL called incremental self-improvement [METARL2] for general purpose RL machines with a single life consisting of a single lifelong trial. That is, unlike in traditional RL, there is no assumption of repeatable independent trials, and the RL agent is never reset. It is driven by a self-modifying policy (SMP) which is a modifiable probability distribution over programs written in a universal programming language [GOD][GOD34][CHU][TUR][POS], to allow for arbitrary computations. The learning algorithm of an SMP is part of the SMP itself—SMPs can modify the way they modify themselves. The credit assignment process has to take into account that early self-modifications are setting the stage for later ones.

A method called Environment-Independent Reinforcement Acceleration (EIRA) [METARL4] or Success-Story Algorithm [METARL7-9] forces SMPs to come up with better and better self-modification algorithms that continually improve reward intake per time [METARL2-9]. This worked well in challenging experiments, although compute back then was 100,000 times more expensive than today. See talk slides (2003) or N(eur)IPS WS 2018 overview slides.

---

3. Gradient-Based NNs Learn to Program Other NNs (1991) and Themselves (1992)

---

Successful learning in deep architectures started in 1965 when Ivakhnenko & Lapa published the first general, working learning algorithms for deep multilayer perceptrons with arbitrarily many hidden layers. Their nets already contained the now popular multiplicative gates [DEEP1-2] [DL1] [DL2], an essential ingredient of what was later called NNs with dynamic links or fast weights. In 1981, v. d. Malsburg was the first to explicitly emphasize the importance of NNs with such rapidly changing connections [FAST]; others followed [T22].

However, these authors did not yet have an end-to-end differentiable system that learns by gradient descent to quickly manipulate the fast weight storage. Such a system I published in 1991 [FWP0] [FWP1]. There a slow NN learns to control the weight changes of a separate fast NN. That is, I separated storage and control like in traditional computers, but in a fully neural way (rather than in a hybrid fashion [PDA1] [PDA2] [DNC]). (Compare my related work on what's now sometimes called Synthetic Gradients [NAN1-5].)

Then I showed how fast weights can be used for meta-learning or "learning to learn." In references [FWPMETA1-5] since 1992, the slow RNN and the fast RNN are identical. The RNN can see its own errors or reward signals called eval(t+1) in the image (from [FWPMETA5]). The initial weight of each connection is trained by gradient descent, but during a training episode, each connection can be addressed and read and modified by the RNN itself through O(log n) special output units, where n is the number of connections—see time-dependent vectors mod(t), anal(t), Δ(t), val(t+1) in the image. That is, each connection's weight may rapidly change, and the network becomes self-referential in the sense that it can in principle run arbitrary computable weight change algorithms or learning algorithms (for all of its weights) on itself.

In 1991-93, I simplified this through gradient descent-based, active control of fast weights through 2D tensors or outer product updates [FWP2] (compare our more recent work on this [FWP3] [FWP3a]). One motivation was to get many more temporal variables under massively parallel end-to-end differentiable control than what's possible in standard RNNs of the same size: O(H²) instead of O(H), where H is the number of hidden units (compare Sec. 8 of [MIR] and item (7) of Sec. XVII of [T22]). The 1993 paper [FWP2] also explicitly addressed the learning of internal spotlights of attention in end-to-end differentiable networks [FWP2] [ATT].

Transformers with "linearized self-attention" [TR1-6] are formally equivalent to my 1991 Fast Weight Programmers [FWP0-1,6][MOST].

In 2001, my former student Sepp Hochreiter used gradient descent in LSTM networks [LSTM1] instead of traditional RNNs to metalearn fast online learning algorithms for nontrivial classes of functions, such as all quadratic functions of two variables [HO1].

Today, the most famous end-to-end differentiable fast weight-based NN [FWP0] is actually our vanilla LSTM network of 2000 [LSTM2] (compare Sec. 4 & Sec. 8 of [MIR]), whose forget gates learn to control the fast weights on self-recurrent connections of internal LSTM cells. All the major IT companies are now massively using vanilla LSTM [DL4].

---

4. Asymptotically Optimal Metalearning for Curriculum Learning (2002-)

---

In 2002, I introduced a general and asymptotically time-optimal type of curriculum learning, that is, solving one problem after another, efficiently searching the space of programs that compute solution candidates, including those programs that organize and manage and adapt and reuse earlier acquired knowledge [OOPS1-3]. The Optimal Ordered Problem Solver (OOPS) draws inspiration from Levin's Universal Search [OPT] designed for single problems. It spends part of the total search time for a new problem on testing programs that exploit previous solution-computing programs in computable ways. If the new problem can be solved faster by copy-editing/invoking previous code than by solving the new problem from scratch, then OOPS will find this out. If not, then at least the previous solutions will not cause much harm. I introduced an efficient, recursive, backtracking-based way of implementing OOPS on realistic computers with limited storage. Experiments illustrated how OOPS can greatly profit from metalearning or metasearching, that is, searching for faster search procedures [OOPS1-2]. The image shows my poster on OOPS at N(eur)IPS 2003.

---

5. Self-Improving Gödel Machine (2003-)

---

The self-referential meta-RL system of Sec. 2 above (1994-) justified its self-modifications through growing statistical evidence of subsequent reward accelerations. But it was not guaranteed to execute theoretically optimal self-improvements. This motivated my Gödel Machine [GM3-9], which was the first fully self-referential universal [UNI] metalearner that was indeed optimal in a certain mathematical sense. Typically it uses the somewhat less general Optimal Ordered Problem Solver [OOPS1-2] (Sec. 4) for finding provably optimal self-improvements.

The metalearning Gödel Machine is inspired by Kurt Gödel, the founder of theoretical computer science in the early 1930s [GOD][GOD34][GOD21,a,b]. He introduced a universal coding language based on the integers which allows for formalizing the operations of any digital computer in axiomatic form. Gödel used it to represent both data (such as axioms and theorems) and programs (such as proof-generating sequences of operations on the data). He famously constructed formal statements that talk about the computation of other formal statements, especially self-referential statements which imply that their truth is not decidable by any computational theorem prover. Thus he identified fundamental limits of mathematics and theorem proving and computing and Artificial Intelligence (AI) [GOD][GOD21,a,b]. This had enormous impact on science and philosophy of the 20th century. Furthermore, much of early AI in the 1940s-70s was actually about theorem proving and deduction in Gödel style through expert systems and logic programming. Compare Sec. 18 of [MIR] and Sec. IV of [T22].

A Gödel Machine [GM6] is a general RL machine that will rewrite any part of its own code as soon as it has found a proof that the rewrite is useful, where the problem-dependent utility function and the hardware and the entire initial code are described by axioms encoded in an initial proof searcher which is also part of the initial code. While the machine is interacting with its environment (initially in a suboptimal way), the searcher systematically and efficiently tests computable proof techniques (programs whose outputs are proofs) until it finds a provably useful, computable self-rewrite. I showed that such a self-rewrite is globally optimal—no local maxima!—since the code first had to prove that it is not useful to continue the proof search for alternative self-rewrites. Unlike previous non-self-referential methods based on hardwired proof searchers, the Gödel Machine not only boasts an optimal order of complexity but can optimally reduce any slowdowns hidden by the O()-notation, provided the utility of such speed-ups is provable at all [GM3-9].

---

6. Meta-RL plus Artificial Curiosity and Intrinsic Motivation (1990, 1997-)

---

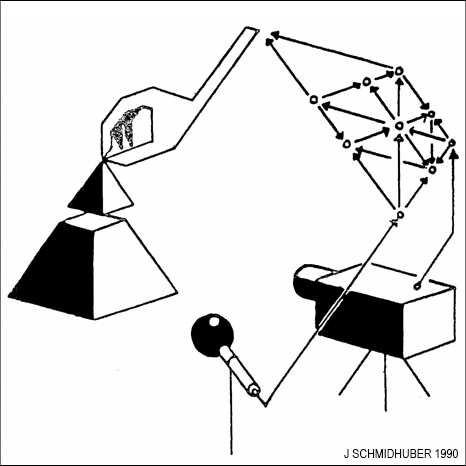The Section "A Connection to Meta-Learning" in [AC90] (1990) already pointed out: "A model network can be used not only for predicting the controller's inputs but also for predicting its future outputs. A perfect model of this kind would model the internal changes of the control network. It would predict the evolution of the controller, and thereby the effects of the gradient descent procedure itself. In this case, the flow of activation in the model network would model the weight changes of the control network. This in turn comes close to the notion of learning how to learn." The paper [AC90] also introduced planning with recurrent NNs (RNNs) as world models [PLAN,PLAN2-5], and high-dimensional reward signals. Unlike in traditional RL, those reward signals were also used as informative inputs to the controller NN learning to execute actions that maximise cumulative reward (see also Sec. 13 of [MIR] and Sec. 5 of [DEC]). This is important for metalearning: an NN that cannot see its own errors or rewards cannot learn a better way of using such signals as inputs for self-invented learning algorithms.

A few years later, I combined the Meta-RL of Sec. 2 and Adversarial Artificial Curiosity in a single system [AC97, AC99, AC02]. It generates computational experiments in form of programs whose execution may change both an external environment and the RL agent's internal state. An experiment has a binary outcome: either a particular effect happens, or it doesn't. Experiments are collectively proposed by two reward-maximizing adversarial policies. Both can predict and bet on experimental outcomes before they happen. Once such an outcome is actually observed, the winner will get a positive reward proportional to the bet, and the loser a negative reward of equal magnitude. So each policy is motivated to create experiments whose yes/no outcomes surprise the other policy. The latter in turn is motivated to learn something about the world that it did not yet know, such that it is not outwitted again.

Using Meta-RL with self-modifying policies [METARL2-9] (Sec. 2), the system learns when to learn and what to learn [AC97, AC99, AC02]. It will also minimize the computational cost of learning new skills, provided both brains receive a small negative reward for each computational step, which introduces a bias towards simple still surprising experiments (reflecting simple still unsolved problems). This may facilitate hierarchical construction of more and more complex experiments, including those yielding external reward (if there is any). In fact, this type of artificial creativity may not only drive artificial scientists and artists [AC06-09], but can also accelerate the intake of external reward [AC97] [AC02], intuitively because a better understanding of the world can help to solve certain problems faster.

The more recent, intrinsically motivated PowerPlay RL system (2011) [PP] [PP1] can use the meatalearning OOPS [OOPS1-2] (Sec. 4) to continually invent on its own new goals and tasks, incrementally learning to become a more and more general problem solver in an active, partially unsupervised or self-supervised fashion. RL robots with high-dimensional video inputs and intrinsic motivation (like in PowerPlay) learned to explore in 2015 [PP2].

---

7. Most Recent Work on Metalearning (2020-2022)

---

My PhD student Imanol Schlag et al. [FWPMETA7] augmented an LSTM with an associative Fast Weight Memory (FWM). Through differentiable operations at every step of a given input sequence, the LSTM updates and maintains compositional associations of former observations stored in the rapidly changing FWM weights. The model is trained end-to-end by gradient descent and yields excellent performance on compositional language reasoning problems, small-scale word-level language modelling, and meta-RL for partially observable environments [FWPMETA7].

Our recent MetaGenRL (2020) [METARL10] meta-learns novel RL algorithms applicable to environments that significantly differ from those used for training. MetaGenRL searches the space of low-complexity loss functions that describe such learning algorithms. See the blog post of my PhD student Louis Kirsch.

This principle of searching for simple learning algorithms is also applicable to fast weight architectures. Our recent Variable Shared Meta Learning (VS-ML) merges weight sharing and sparsity in meta-learning RNNs [FWPMETA6]. This allows for encoding the learning algorithm by few parameters although it has many time-varying variables—compare [FWP2] (Sec. 3). VS-ML combines end-to-end differentiable fast weights [FWP1-3a] (Sec. 3) and learning algorithms encoded in the activations of LSTMs [HO1]. Some of these activations can be interpreted as NN weights updated by the LSTM dynamics. LSTMs with shared sparse entries in their weight matrix discover learning algorithms that generalize to new datasets. The meta-learned learning algorithms do not require explicit gradient calculation. VS-ML in RNNs can also learn to implement the famous backpropagation learning algorithm [BP1] [BP2] [BP4] purely in the end-to-end differentiable forward dynamics of RNNs [FWPMETA6].

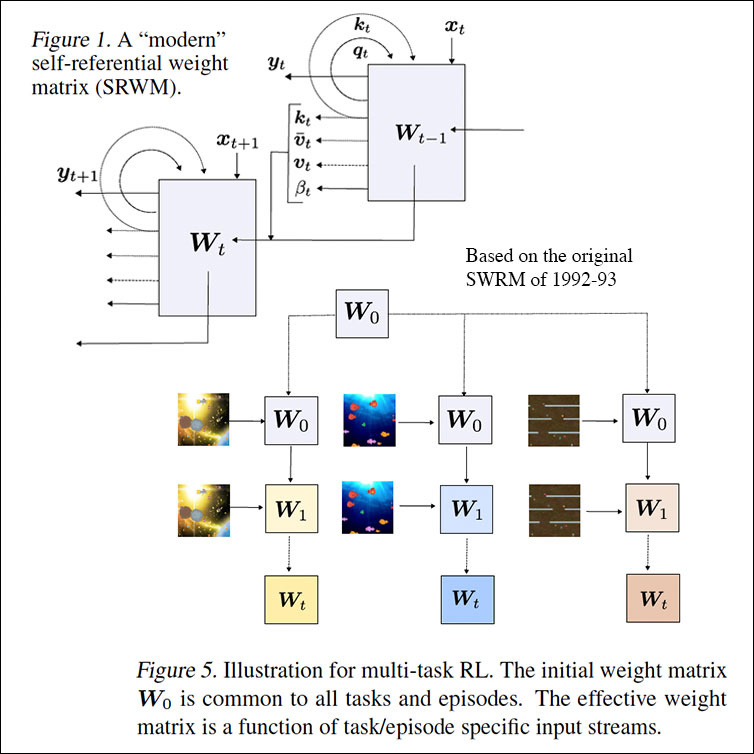
In 2022, we also published at ICML a modern self-referential weight matrix (SWRM) [FWPMETA8] based on the 1992 SWRM [FWPMETA1-5] (see Sec. 3). In principle, it can meta-learn to learn, and meta-meta-learn to meta-learn to learn, and so on, in the sense of recursive self-improvement (compare this tweet). We evaluated our SRWM on supervised few-shot learning tasks and on multi-task reinforcement learning with procedurally generated game environments. The experiments demonstrated both practical applicability and competitive performance of the SRWM.

Acknowledgments

---

Thanks to several expert reviewers for useful comments. Since science is about self-correction, let me know under juergen@idsia.ch if you can spot any remaining error. The contents of this article may be used for educational and non-commercial purposes, including articles for Wikipedia and similar sites. This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

---

References

---

[AC] J.  Schmidhuber (AI Blog, 2021). 3 decades of artificial curiosity & creativity. Our artificial scientists not only answer given questions but also invent new questions. They achieve curiosity through: (1990) the principle of generative adversarial networks, (1991) neural nets that maximise learning progress, (1995) neural nets that maximise information gain (optimally since 2011), (1997) adversarial design of surprising computational experiments, (2006) maximizing compression progress like scientists/artists/comedians do, (2011) PowerPlay... Since 2012: applications to real robots.

[AC90] J.  Schmidhuber. Making the world differentiable: On using fully recurrent self-supervised neural networks for dynamic reinforcement learning and planning in non-stationary environments. Technical Report FKI-126-90, TUM, Feb 1990, revised Nov 1990. PDF

[AC90b] J.  Schmidhuber. A possibility for implementing curiosity and boredom in model-building neural controllers. In J. A. Meyer and S. W. Wilson, editors, Proc. of the International Conference on Simulation of Adaptive Behavior: From Animals to Animats, pages 222-227. MIT Press/Bradford Books, 1991. PDF. HTML.

[AC91] J. Schmidhuber. Adaptive confidence and adaptive curiosity. Technical Report FKI-149-91, Inst. f. Informatik, Tech. Univ. Munich, April 1991. PDF.

[AC91b] J.  Schmidhuber. Curious model-building control systems. In Proc. International Joint Conference on Neural Networks, Singapore, volume 2, pages 1458-1463. IEEE, 1991. PDF.

[AC95] J. Storck, S. Hochreiter, and J. Schmidhuber. Reinforcement-driven information acquisition in non-deterministic environments. In Proc. ICANN'95, vol. 2, pages 159-164. EC2 & CIE, Paris, 1995. PDF.

[AC97] J. Schmidhuber. What's interesting? Technical Report IDSIA-35-97, IDSIA, July 1997.

[AC99] J. Schmidhuber. Artificial Curiosity Based on Discovering Novel Algorithmic Predictability Through Coevolution. In P. Angeline, Z. Michalewicz, M. Schoenauer, X. Yao, Z. Zalzala, eds., Congress on Evolutionary Computation, p. 1612-1618, IEEE Press, Piscataway, NJ, 1999.

[AC02] J. Schmidhuber. Exploring the Predictable. In Ghosh, S. Tsutsui, eds., Advances in Evolutionary Computing, p. 579-612, Springer, 2002. PDF.

[AC06] J.  Schmidhuber. Developmental Robotics, Optimal Artificial Curiosity, Creativity, Music, and the Fine Arts. Connection Science, 18(2): 173-187, 2006. PDF.

[AC09] J. Schmidhuber. Art & science as by-products of the search for novel patterns, or data compressible in unknown yet learnable ways. In M. Botta (ed.), Et al. Edizioni, 2009, pp. 98-112. PDF. (More on artificial scientists and artists.)

[AC10] J. Schmidhuber. Formal Theory of Creativity, Fun, and Intrinsic Motivation (1990-2010). IEEE Transactions on Autonomous Mental Development, 2(3):230-247, 2010. IEEE link. PDF.

[AC20] J. Schmidhuber. Generative Adversarial Networks are Special Cases of Artificial Curiosity (1990) and also Closely Related to Predictability Minimization (1991). Neural Networks, Volume 127, p 58-66, 2020. Preprint arXiv/1906.04493.

[ATT] J. Schmidhuber (AI Blog, 2020). 30-year anniversary of end-to-end differentiable sequential neural attention. Plus goal-conditional reinforcement learning. We had both hard attention (1990) and soft attention (1991-93).^[FWP] Today, both types are very popular.

[BP1] S. Linnainmaa. The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors. Master's Thesis (in Finnish), Univ. Helsinki, 1970. See chapters 6-7 and FORTRAN code on pages 58-60. PDF. See also BIT 16, 146-160, 1976. Link.

[BPA] H. J. Kelley. Gradient Theory of Optimal Flight Paths. ARS Journal, Vol. 30, No. 10, pp. 947-954, 1960.

[BP2] P. J. Werbos. Applications of advances in nonlinear sensitivity analysis. In R. Drenick, F. Kozin, (eds): System Modeling and Optimization: Proc. IFIP, Springer, 1982. PDF. [Extending thoughts in his 1974 thesis.]

[BP4] J. Schmidhuber (AI Blog, 2014; updated 2020). Who invented backpropagation? More.^[DL2]

[CHU] A. Church (1935). An unsolvable problem of elementary number theory. Bulletin of the American Mathematical Society, 41: 332-333. Abstract of a talk given on 19 April 1935, to the American Mathematical Society. Also in American Journal of Mathematics, 58(2), 345-363 (1 Apr 1936). First explicit proof that the Entscheidungsproblem (decision problem) does not have a general solution.

[DEC] J. Schmidhuber (AI Blog, 02/20/2020, revised 2021). The 2010s: Our Decade of Deep Learning / Outlook on the 2020s. The recent decade's most important developments and industrial applications based on our AI, with an outlook on the 2020s, also addressing privacy and data markets.

[DEEP1] Ivakhnenko, A. G. and Lapa, V. G. (1965). Cybernetic Predicting Devices. CCM Information Corporation. First working Deep Learners with many layers, learning internal representations.

[DEEP1a] Ivakhnenko, Alexey Grigorevich. The group method of data of handling; a rival of the method of stochastic approximation. Soviet Automatic Control 13 (1968): 43-55.

[DEEP2] Ivakhnenko, A. G. (1971). Polynomial theory of complex systems. IEEE Transactions on Systems, Man and Cybernetics, (4):364-378.

[DL1] J. Schmidhuber, 2015. Deep learning in neural networks: An overview. Neural Networks, 61, 85-117. More. Got the first Best Paper Award ever issued by the journal Neural Networks, founded in 1988.

[DL2] J. Schmidhuber, 2015. Deep Learning. Scholarpedia, 10(11):32832.

[DL4] J. Schmidhuber (AI Blog, 2017). Our impact on the world's most valuable public companies: Apple, Google, Microsoft, Facebook, Amazon... By 2015-17, neural nets developed in my labs were on over 3 billion devices such as smartphones, and used many billions of times per day, consuming a significant fraction of the world's compute. Examples: greatly improved (CTC-based) speech recognition on all Android phones, greatly improved machine translation through Google Translate and Facebook (over 4 billion LSTM-based translations per day), Apple's Siri and Quicktype on all iPhones, the answers of Amazon's Alexa, etc. Google's 2019 on-device speech recognition (on the phone, not the server) is still based on LSTM.

[DL6] F. Gomez and J. Schmidhuber. Co-evolving recurrent neurons learn deep memory POMDPs. In Proc. GECCO'05, Washington, D. C., pp. 1795-1802, ACM Press, New York, NY, USA, 2005. PDF.

[DL6a] J. Schmidhuber (AI Blog, Nov 2020). 15-year anniversary: 1st paper with "learn deep" in the title (2005). Our deep reinforcement learning & neuroevolution solved problems of depth 1000 and more.^[DL6] Soon after its publication, everybody started talking about "deep learning." Causality or correlation?

[DNC] Hybrid computing using a neural network with dynamic external memory. A. Graves, G. Wayne, M. Reynolds, T. Harley, I. Danihelka, A. Grabska-Barwinska, S. G. Colmenarejo, E. Grefenstette, T. Ramalho, J. Agapiou, A. P. Badia, K. M. Hermann, Y. Zwols, G. Ostrovski, A. Cain, H. King, C. Summerfield, P. Blunsom, K. Kavukcuoglu, D. Hassabis. Nature, 538:7626, p 471, 2016.

[FAST] C. v.d. Malsburg. Tech Report 81-2, Abteilung f. Neurobiologie, Max-Planck Institut f. Biophysik und Chemie, Goettingen, 1981. First paper on fast weights or dynamic links.

[FASTa] J. A. Feldman. Dynamic connections in neural networks. Biological Cybernetics, 46(1):27-39, 1982. 2nd paper on fast weights.

[FWP] J.  Schmidhuber (AI Blog, 26 March 2021). 26 March 1991: Neural nets learn to program neural nets with fast weights—like Transformer variants. 2021: New stuff! 30-year anniversary of a now popular alternative^[FWP0-1] to recurrent NNs. A slow feedforward NN learns by gradient descent to program the changes of the fast weights^[FAST,FASTa] of another NN. Such Fast Weight Programmers^{[FWP0-6,FWPMETA1-7]} can learn to memorize past data, e.g., by computing fast weight changes through additive outer products of self-invented activation patterns^[FWP0-1] (now often called keys and values for self-attention^[TR1-6]). The similar Transformers^[TR1-2] combine this with projections and softmax and are now widely used in natural language processing. For long input sequences, their efficiency was improved through Transformers with linearized self-attention^[TR5-6] which are formally equivalent to the 1991 Fast Weight Programmers (apart from normalization). In 1993, I introduced the attention terminology^[FWP2] now used in this context,^[ATT] and extended the approach to RNNs that program themselves.

[FWP0] J.  Schmidhuber. Learning to control fast-weight memories: An alternative to recurrent nets. Technical Report FKI-147-91, Institut für Informatik, Technische Universität München, March 1991. PDF.

[FWP1] J. Schmidhuber. Learning to control fast-weight memories: An alternative to recurrent nets. Neural Computation, 4(1):131-139, 1992. PDF. HTML. Pictures (German).

[FWP2] J. Schmidhuber. Reducing the ratio between learning complexity and number of time-varying variables in fully recurrent nets. In Proceedings of the International Conference on Artificial Neural Networks, Amsterdam, pages 460-463. Springer, 1993. PDF.

[FWP3] I. Schlag, J. Schmidhuber. Gated Fast Weights for On-The-Fly Neural Program Generation. Workshop on Meta-Learning, @N(eur)IPS 2017, Long Beach, CA, USA.

[FWP3a] I. Schlag, J. Schmidhuber. Learning to Reason with Third Order Tensor Products. Advances in Neural Information Processing Systems (N(eur)IPS), Montreal, 2018. Preprint: arXiv:1811.12143. PDF.

[FWP5] F. J. Gomez and J. Schmidhuber. Evolving modular fast-weight networks for control. In W. Duch et al. (Eds.): Proc. ICANN'05, LNCS 3697, pp. 383-389, Springer-Verlag Berlin Heidelberg, 2005. PDF. HTML overview. Reinforcement-learning fast weight programmer.

[FWP6] I. Schlag, K. Irie, J. Schmidhuber. Linear Transformers Are Secretly Fast Weight Programmers. ICML 2021. Preprint: arXiv:2102.11174.

[FWP7] K. Irie, I. Schlag, R. Csordas, J. Schmidhuber. Going Beyond Linear Transformers with Recurrent Fast Weight Programmers. Preprint: arXiv:2106.06295 (June 2021).

[FWPMETA1] J. Schmidhuber. Steps towards `self-referential' learning. Technical Report CU-CS-627-92, Dept. of Comp. Sci., University of Colorado at Boulder, November 1992. PDF.

[FWPMETA2] J. Schmidhuber. A self-referential weight matrix. In Proceedings of the International Conference on Artificial Neural Networks, Amsterdam, pages 446-451. Springer, 1993. PDF.

[FWPMETA3] J. Schmidhuber. An introspective network that can learn to run its own weight change algorithm. In Proc. of the Intl. Conf. on Artificial Neural Networks, Brighton, pages 191-195. IEE, 1993.

[FWPMETA4] J.  Schmidhuber. A neural network that embeds its own meta-levels. In Proc. of the International Conference on Neural Networks '93, San Francisco. IEEE, 1993.

[FWPMETA5] J. Schmidhuber. Habilitation thesis, TUM, 1993. PDF. [A recurrent neural net with a self-referential, self-reading, self-modifying weight matrix can be found here.]

[FWPMETA6] L. Kirsch and J. Schmidhuber. Meta Learning Backpropagation & Improving It. Metalearning Workshop at NeurIPS, 2020. Preprint arXiv:2012.14905 [cs.LG], 2020.

[FWPMETA7] I. Schlag, T. Munkhdalai, J. Schmidhuber. Learning Associative Inference Using Fast Weight Memory. Report arXiv:2011.07831 [cs.AI], 2020.

[FWPMETA8] K. Irie, I. Schlag, R. Csordas, J. Schmidhuber. A Modern Self-Referential Weight Matrix That Learns to Modify Itself. International Conference on Machine Learning (ICML), 2022. Preprint: arXiv:2202.05780.

[FWPMETA9] L. Kirsch and J. Schmidhuber. Self-Referential Meta Learning. First Conference on Automated Machine Learning (Late-Breaking Workshop), 2022.

[GM3] J. Schmidhuber (2003). Goedel Machines: Self-Referential Universal Problem Solvers Making Provably Optimal Self-Improvements. Preprint arXiv:cs/0309048 (2003). More.

[GM6] J. Schmidhuber (2006). Gödel machines: Fully Self-Referential Optimal Universal Self-Improvers. In B. Goertzel and C. Pennachin, eds.: Artificial General Intelligence, p. 199-226, 2006. PDF.

[GM9] J. Schmidhuber (2009). Ultimate Cognition à la Gödel. Cognitive Computation 1(2):177-193, 2009. PDF. More.

[GOD] K. Gödel. Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für Mathematik und Physik, 38:173-198, 1931. [In the early 1930s, Gödel founded theoretical computer science. He identified fundamental limits of mathematics and theorem proving and computing and Artificial Intelligence.]

[GOD34] K. Gödel (1934). On undecidable propositions of formal mathematical systems. Notes by S. C. Kleene and J. B. Rosser on lectures at the Institute for Advanced Study, Princeton, New Jersey, 1934, 30 pp. (Reprinted in M. Davis, (ed.), The Undecidable. Basic Papers on Undecidable Propositions, Unsolvable Problems, and Computable Functions, Raven Press, Hewlett, New York, 1965.) [Gödel introduced a universal coding language.]

[GOD21] J. Schmidhuber (AI Blog, 2021). 90th anniversary celebrations: 1931: Kurt Gödel, founder of theoretical computer science, shows limits of math, logic, computing, and artificial intelligence. This was number 1 on Hacker News.

[GOD21a] J. Schmidhuber (2021). Als Kurt Gödel die Grenzen des Berechenbaren entdeckte. (When Kurt Gödel discovered the limits of computability.) Frankfurter Allgemeine Zeitung, 16/6/2021.

[GOD21b] J. Schmidhuber (AI Blog, 2021). 80. Jahrestag: 1931: Kurt Gödel, Vater der theoretischen Informatik, entdeckt die Grenzen des Berechenbaren und der künstlichen Intelligenz.

[GP87] D. Dickmanns, J. Schmidhuber, A. Winklhofer: Der genetische Algorithmus: Eine Implementierung in Prolog. Fortgeschrittenenpraktikum, Institut f. Informatik, Lehrstuhl Prof. Radig, Tech. Univ. Munich, 1987. Probably the first work on Genetic Programming for evolving programs of unlimited size written in a universal coding language. Based on work I did since 1985 on a Symbolics Lisp Machine of SIEMENS AG. Authors in alphabetical order. More.

[GP] J. Schmidhuber, 2020. Genetic Programming for code of unlimited size (1987)

[HO1] S. Hochreiter, A. S. Younger, P. R. Conwell (2001). Learning to Learn Using Gradient Descent. ICANN 2001. Lecture Notes in Computer Science, 2130, pp. 87-94.

[LEC] J. Schmidhuber (AI Blog, 2022). LeCun's 2022 paper on autonomous machine intelligence rehashes but does not cite essential work of 1990-2015. Years ago we published most of what LeCun calls his "main original contributions:" neural nets that learn multiple time scales and levels of abstraction, generate subgoals, use intrinsic motivation to improve world models, and plan (1990); controllers that learn informative predictable representations (1997), etc. This was also discussed on Hacker News, reddit, and various media.

[LSTM1] S. Hochreiter, J. Schmidhuber. Long Short-Term Memory. Neural Computation, 9(8):1735-1780, 1997. PDF. Based on [LSTM0]. More.

[LSTM2] F. A. Gers, J. Schmidhuber, F. Cummins. Learning to Forget: Continual Prediction with LSTM. Neural Computation, 12(10):2451-2471, 2000. PDF. The "vanilla LSTM architecture" with forget gates that everybody is using today, e.g., in Google's Tensorflow.

[META] J. Schmidhuber (AI Blog, 2020). 1/3 century anniversary of first publication on metalearning machines that learn to learn (1987). For its cover I drew a robot that bootstraps itself. 1992-: gradient descent-based neural metalearning. 1994-: Meta-Reinforcement Learning with self-modifying policies. 1997: Meta-RL plus artificial curiosity and intrinsic motivation. 2002-: asymptotically optimal metalearning for curriculum learning. 2003-: mathematically optimal Gödel Machine. 2020: new stuff!

[META1] J.  Schmidhuber. Evolutionary principles in self-referential learning, or on learning how to learn: The meta-meta-... hook. Diploma thesis, Institut für Informatik, Technische Universität München, 1987. Searchable PDF scan (created by OCRmypdf which uses LSTM). HTML. For example, Genetic Programming (GP) is applied to itself, to recursively evolve better GP methods through Meta-Evolution. More.

[META10] T. Schaul and J. Schmidhuber. Metalearning. Scholarpedia, 5(6):4650, 2010.

[METARL2] J. Schmidhuber. On learning how to learn learning strategies. Technical Report FKI-198-94, Fakultät für Informatik, Technische Universität München, November 1994. PDF.

[METARL3] J.  Schmidhuber. Beyond "Genetic Programming": Incremental Self-Improvement. In J. Rosca, ed., Proc. Workshop on Genetic Programming at ML95, pages 42-49. National Resource Lab for the study of Brain and Behavior, 1995.

[METARL4] M. Wiering and J. Schmidhuber. Solving POMDPs using Levin search and EIRA. In L. Saitta, ed., Machine Learning: Proceedings of the 13th International Conference (ICML 1996), pages 534-542, Morgan Kaufmann Publishers, San Francisco, CA, 1996. PDF. HTML.

[METARL5] J.  Schmidhuber and J.  Zhao and M.  Wiering. Simple principles of metalearning. Technical Report IDSIA-69-96, IDSIA, June 1996. PDF.

[METARL6] J.  Zhao and J.  Schmidhuber. Solving a complex prisoner's dilemma with self-modifying policies. In From Animals to Animats 5: Proceedings of the Fifth International Conference on Simulation of Adaptive Behavior, 1998.

[METARL7] Shifting inductive bias with success-story algorithm, adaptive Levin search, and incremental self-improvement. Machine Learning 28:105-130, 1997. PDF.

[METARL8] J.  Schmidhuber, J.  Zhao, N. Schraudolph. Reinforcement learning with self-modifying policies. In S. Thrun and L. Pratt, eds., Learning to learn, Kluwer, pages 293-309, 1997. PDF; HTML.

[METARL9] A general method for incremental self-improvement and multiagent learning. In X. Yao, editor, Evolutionary Computation: Theory and Applications. Chapter 3, pp.81-123, Scientific Publ. Co., Singapore, 1999.

[METARL10] L. Kirsch, S. van Steenkiste, J. Schmidhuber. Improving Generalization in Meta Reinforcement Learning using Neural Objectives. International Conference on Learning Representations, 2020.

[MIR] J. Schmidhuber (AI Blog, 2019). Deep Learning: Our Miraculous Year 1990-1991. Preprint arXiv:2005.05744, 2020. The deep learning neural networks of our team have revolutionised pattern recognition and machine learning, and are now heavily used in academia and industry. In 2020-21, we celebrate that many of the basic ideas behind this revolution were published within fewer than 12 months in our "Annus Mirabilis" 1990-1991 at TU Munich.

[MOST] J.  Schmidhuber (AI Blog, 2021). The most cited neural networks all build on work done in my labs. Foundations of the most popular NNs originated in my labs at TU Munich and IDSIA. Here I mention: (1) Long Short-Term Memory (LSTM), (2) ResNet (which is our earlier Highway Net with open gates), (3) AlexNet and VGG Net (both building on our similar earlier DanNet: the first deep convolutional NN to win image recognition competitions), (4) Generative Adversarial Networks (an instance of my earlier Adversarial Artificial Curiosity), and (5) variants of Transformers (linear Transformers are formally equivalent to my earlier Fast Weight Programmers). Most of this started with our Annus Mirabilis of 1990-1991.^[MIR]

[NAN1] J.  Schmidhuber. Networks adjusting networks. In J. Kindermann and A. Linden, editors, Proceedings of `Distributed Adaptive Neural Information Processing', St.Augustin, 24.-25.5. 1989, pages 197-208. Oldenbourg, 1990. Extended version: TR FKI-125-90 (revised), Institut für Informatik, TUM. PDF.

[NAN2] J.  Schmidhuber. Networks adjusting networks. Technical Report FKI-125-90, Institut für Informatik, Technische Universität München. Revised in November 1990. PDF.

[NAN3] Recurrent networks adjusted by adaptive critics. In Proc. IEEE/INNS International Joint Conference on Neural Networks, Washington, D. C., volume 1, pages 719-722, 1990.

[NAN4] J. Schmidhuber. Additional remarks on G. Lukes' review of Schmidhuber's paper `Recurrent networks adjusted by adaptive critics'. Neural Network Reviews, 4(1):43, 1990.

[NAN5] M. Jaderberg, W. M. Czarnecki, S. Osindero, O. Vinyals, A. Graves, D. Silver, K. Kavukcuoglu. Decoupled Neural Interfaces using Synthetic Gradients. Preprint arXiv:1608.05343, 2016.

[OOPS1] J. Schmidhuber. Bias-Optimal Incremental Problem Solving. In S. Becker, S. Thrun, K. Obermayer, eds., Advances in Neural Information Processing Systems 15, N(eur)IPS'15, MIT Press, Cambridge MA, p. 1571-1578, 2003. PDF

[OOPS2] J. Schmidhuber. Optimal Ordered Problem Solver. Machine Learning, 54, 211-254, 2004. PDF. HTML. HTML overview. Download OOPS source code in crystalline format.

[OOPS3] Schmidhuber, J., Zhumatiy, V. and Gagliolo, M. Bias-Optimal Incremental Learning of Control Sequences for Virtual Robots. In Groen, F., Amato, N., Bonarini, A., Yoshida, E., and Kroese, B., editors: Proceedings of the 8-th conference on Intelligent Autonomous Systems, IAS-8, Amsterdam, The Netherlands, pp. 658-665, 2004. PDF.

[OPT] J. Schmidhuber (2004). Optimal Universal Search.

[PDA1] G.Z. Sun, H.H. Chen, C.L. Giles, Y.C. Lee, D. Chen. Neural Networks with External Memory Stack that Learn Context - Free Grammars from Examples. Proceedings of the 1990 Conference on Information Science and Systems, Vol.II, pp. 649-653, Princeton University, Princeton, NJ, 1990.

[PDA2] M. Mozer, S. Das. A connectionist symbol manipulator that discovers the structure of context-free languages. Proc. N(eur)IPS 1993.

[PLAN] J. Schmidhuber (AI Blog, 2020). 30-year anniversary of planning & reinforcement learning with recurrent world models and artificial curiosity (1990). This work also introduced high-dimensional reward signals, deterministic policy gradients for RNNs, the GAN principle (widely used today). Agents with adaptive recurrent world models even suggest a simple explanation of consciousness & self-awareness.

[PLAN2] J.  Schmidhuber. An on-line algorithm for dynamic reinforcement learning and planning in reactive environments. In Proc. IEEE/INNS International Joint Conference on Neural Networks, San Diego, volume 2, pages 253-258, June 17-21, 1990. Based on [AC90].

[PLAN3] J.  Schmidhuber. Reinforcement learning in Markovian and non-Markovian environments. In D. S. Lippman, J. E. Moody, and D. S. Touretzky, editors, Advances in Neural Information Processing Systems 3, N(eur)IPS'3, pages 500-506. San Mateo, CA: Morgan Kaufmann, 1991. PDF. Partially based on [AC90].

[PLAN4] J. Schmidhuber. On Learning to Think: Algorithmic Information Theory for Novel Combinations of Reinforcement Learning Controllers and Recurrent Neural World Models. Report arXiv:1210.0118 [cs.AI], 2015.

[PLAN5] One Big Net For Everything. Preprint arXiv:1802.08864 [cs.AI], Feb 2018.

[PLAN6] D. Ha, J. Schmidhuber. Recurrent World Models Facilitate Policy Evolution. Advances in Neural Information Processing Systems (N(eur)IPS), Montreal, 2018. (Talk.) Preprint: arXiv:1809.01999. Github: World Models.

[POS] E. L. Post (1936). Finite Combinatory Processes - Formulation 1. Journal of Symbolic Logic. 1: 103-105. Link.

[PP] J. Schmidhuber. POWERPLAY: Training an Increasingly General Problem Solver by Continually Searching for the Simplest Still Unsolvable Problem. Frontiers in Cognitive Science, 2013. ArXiv preprint (2011): arXiv:1112.5309 [cs.AI]

[PP1] R. K. Srivastava, B. Steunebrink, J. Schmidhuber. First Experiments with PowerPlay. Neural Networks, 2013. ArXiv preprint (2012): arXiv:1210.8385 [cs.AI].

[PP2] V. Kompella, M. Stollenga, M. Luciw, J. Schmidhuber. Continual curiosity-driven skill acquisition from high-dimensional video inputs for humanoid robots. Artificial Intelligence, 2015.

[R2] Reddit/ML, 2019. J. Schmidhuber really had GANs in 1990.

[R3] Reddit/ML, 2019. NeurIPS 2019 Bengio Schmidhuber Meta-Learning Fiasco.

[R7] Reddit/ML, 2019. J. Schmidhuber on Seppo Linnainmaa, inventor of backpropagation in 1970.

[T22] J. Schmidhuber (AI Blog, 2022). Scientific Integrity and the History of Deep Learning: The 2021 Turing Lecture, and the 2018 Turing Award. Technical Report IDSIA-77-21 (v3), IDSIA, Lugano, Switzerland, 2021-2022.

[TR1] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser, I. Polosukhin (2017). Attention is all you need. NIPS 2017, pp. 5998-6008.

[TR2] J. Devlin, M. W. Chang, K. Lee, K. Toutanova (2018). Bert: Pre-training of deep bidirectional transformers for language understanding. Preprint arXiv:1810.04805.

[TR3] K. Tran, A. Bisazza, C. Monz. The Importance of Being Recurrent for Modeling Hierarchical Structure. EMNLP 2018, p 4731-4736. ArXiv preprint 1803.03585.

[TR4] M. Hahn. Theoretical Limitations of Self-Attention in Neural Sequence Models. Transactions of the Association for Computational Linguistics, Volume 8, p.156-171, 2020.

[TR5] A. Katharopoulos, A. Vyas, N. Pappas, F. Fleuret. Transformers are RNNs: Fast autoregressive Transformers with linear attention. In Proc. Int. Conf. on Machine Learning (ICML), July 2020.

[TR6] K. Choromanski, V. Likhosherstov, D. Dohan, X. Song, A. Gane, T. Sarlos, P. Hawkins, J. Davis, A. Mohiuddin, L. Kaiser, et al. Rethinking attention with Performers. In Int. Conf. on Learning Representations (ICLR), 2021.

[TRA12] D. Ciresan, U. Meier, J. Schmidhuber. Transfer Learning for Latin and Chinese Characters with Deep Neural Networks. Proc. IJCNN 2012, p 1301-1306, 2012. PDF.

[TUR] A. M. Turing. On computable numbers, with an application to the Entscheidungsproblem. Proceedings of the London Mathematical Society, Series 2, 41:230-267. Received 28 May 1936. Errata appeared in Series 2, 43, pp 544-546 (1937).

[UNI] J. Schmidhuber (2004). Theory of universal learning machines and universal AI.
.