.
In 2020-21, we celebrate 3 decades of artificial curiosity and creativity with neural world models

Jürgen Schmidhuber (2021, updated 2022, 2023)
Pronounce: YourGAN Shmidhoobuh 		AI Blog
Twitter: @SchmidhuberAI

Artificial Curiosity & Creativity Since 1990-91

Abstract. For over three decades I have published work about artificial scientists equipped with artificial curiosity and creativity.[AC90-AC22][PP-PP2] In this context, I have frequently pointed out that there are two important things in science: (A) Finding answers to given questions, and (B) Coming up with good questions. (A) is arguably just the standard problem of computer science. But how to implement the creative part (B) in artificial systems through reinforcement learning (RL), gradient-based artificial neural networks (NNs), and other machine learning methods? Here I summarise some of our approaches:
Sec. 1. 1990: Curiosity through the principle of generative adversarial networks
Sec. 2. 1991: Curiosity through NNs that maximise learning progress
Sec. 3. 1995: RL to maximise information gain or Bayesian surprise. (2011: Do this optimally)
Sec. 4. 1997: Adversarial RL agents design surprising computational experiments
Sec. 4a. 2022: NNs generating complex experiments encoded as NN weight matrices
Sec. 5. 2006: RL to maximise compression progress like scientists/artists/comedians do
Sec. 6. Does curiosity distort the basic reinforcement learning problem?
Sec. 7. Connections to metalearning since 1990
Sec. 8. 2011: PowerPlay continually searches for novel well-defined computational problems whose solutions can easily be added to the skill repertoire, taking into account verification time
Sec. 9. 2015: Planning and curiosity with spatio-temporal abstractions in NNs

1. 1990: Curiosity through the principle of generative adversarial networks

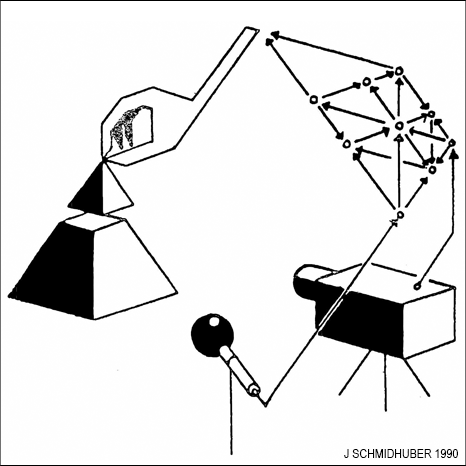
Predictability Minimization: unsupervised minimax game where one neural network minimizes the objective function maximized by another My first artificial Q&A system designed to invent and answer questions was the intrinsic motivation-based adversarial system from 1990.[AC90][AC90b] It employs two artificial neural networks (NNs) that duel each other. The first NN is the controller C. C probabilistically generates outputs that may influence an environment. The second NN is the world model M. It predicts the environmental reactions to C's outputs. Using gradient descent, M minimizes its error, thus becoming a better predictor. But in a zero sum game, the reward-maximizing C tries to find sequences of output actions that maximize the error of M. Thus M's loss is C's gain.

So C is asking questions through its action sequences, e.g., "what happens if I do this?", and M is learning to answer those questions. Here C is motivated to come up with questions where M does not yet know the answer, and C loses interest in questions with known answers. This was the start of a long series of papers on artificial curiosity and artificial scientists.[AC90-AC20][PP-PP2]

My well-known 2010 survey[AC10] summarised the generative adversarial NNs of 1990 as follows: a "neural network as a predictive world model is used to maximize the controller's intrinsic reward, which is proportional to the model's prediction errors" (which are minimized). (Other early adversarial machine learning settings[S59][H90] were very different—they neither involved unsupervised NNs nor were about modeling data nor used gradient descent.[AC20])

Note that instead of predicting the raw data, M may predict compressed versions thereof.[PLAN4] Generally speaking, a curious system may predict abstract internal representations[AC97][AC02][LEC] of raw data (Sec. 4).

High-dimensional reward signals (1990) as inputs of a recurrent neural net controller Not only the 1990s but also more recent years saw successful applications of this simple adversarial principle and its variants in Reinforcement Learning (RL) settings.[SIN5][OUD13][PAT17][BUR18] Q&As help to understand the world which is necessary for planning [PLAN][PLAN2-6][RES5-7] and may boost external reward.[AC91][AC97][AC02][PAT17] [BUR18] In the 2010s, the concepts of 1990 became popular as compute became cheaper.[DEC][LEC][DLH][MOST]

The term generative adversarial networks (GANs) is actually a new name for an instance of the principle published in 1990.[AC90][AC90b][R2][AC20][LEC] GAN trials are extremely short, consisting of a single action and a single environmental reaction, like in bandit problems. In modern GAN terminology, the controller C is called the generator, and the world model M the discriminator. See also[MIR](Sec. 5)[T22](Sec. XVII) and the closely related Predictability Minimization[PM0-2][AC20] (applied to images in 1996[PM2]). There was a priority dispute on GANs discussed in Sec. XVII of Technical Report IDSIA-77-21.[T22]

2. 1991: Curiosity through maximizing learning progress

2015: curious iCub baby robot with camera vision learns new skills through curious exploration The approach of 1990[AC90][AC90b] (Sec. 1) makes for a fine exploration strategy in many deterministic environments. In stochastic environments, however, it might fail. C might learn to focus on those parts of the environment where M can always get high prediction errors due to randomness, or due to computational limitations of M. For example, an agent controlled by C might get stuck in front of a TV screen showing highly unpredictable white noise.[AC10]

Therefore, in stochastic environments, C's reward should not be the errors of M, but an approximation of the first derivative of M's errors across subsequent training iterations, that is, to prevent C from exploiting M too easily, C's reward should be M's learning progress or improvements.[AC91][AC10][PP2] As a consequence, despite M's high errors in front of the noisy TV above, C won't get rewarded for getting stuck there, simply because M's errors won't improve: both the totally predictable and the fundamentally unpredictable will get boring.

3. 1995: RL for maximizing information gain or Bayesian surprise

The simple insight of 1991 (Sec. 2) led to lots of follow-up work.[AC10] One particular reinforcement learning (RL) approach for artificial curiosity in stochastic environments was published in 1995 with my former students Jan Storck and Sepp Hochreiter.[AC95] A simple world model M learned to predict or estimate the probabilities of the environment's possible responses, given the actions of a controller C. After each interaction with the environment, C's intrinsic reward was the KL-Divergence[KUL] between M's estimated probability distributions before and after the resulting new experience, i.e., the information gain.[AC95] 10 years later, this was dubbed Bayesian surprise.[ITT5] Compare earlier work on information gain[SHA] and its maximization through active learning without RL & NNs.[FED]

More formally, at a given time in a single lifelong trial, M has seen the entire history H of C's sensory inputs and actions so far. Now it is trying to predict the next sensory input Q, given H. Suppose there are n possible values Q1, ..., Qn of Q. For 0<i<n+1 (n and i are natural numbers), M predicts the conditional probability pM(Qi|H) of Qi, given H. Then Q is really observed. Now M is trained for some time on the observations so far to improve its predictions. This yields an updated version of M called M*. Q's contribution rint(Q) to C's intrinsic curiosity reward is proportional to ∑i pM*(Qi|H) log (pM*(Qi|H) / pM(Qi|H)), the information gain about Q. C's intrinsic joy is M's current learning progress. Now the history H is prolonged by Q and we set M:=M* such that M is ready to predict the next input observation.

Again, since the controller C is a reward maximizer, C is motivated to invent action sequences or experiments that yield data from which the world model M can still learn something. C will get bored by well-known parts of the environment as well as by unpredictable noisy TVs.[AC10]

2011: Bayes-optimal planning to be surprised. My student Sun Yi et al. showed that C can optimally plan action sequences based on previous experiences such that the cumulative expected information gain is maximized.[AC11]

4. 1997: Adversarial agents design surprising computational experiments

Self-referential problem-solving robot thinking about itself Before 1997, the questions asked by the controller C were restricted in the sense that they always referred to all the details of future inputs, e.g., pixels.[AC90][AC90b] That's why in 1997, I built more general adversarial RL machines that could ignore many or all of these details and ask arbitrary abstract questions with computable answers.[AC97][AC99][AC02][LEC] For example, an agent may ask: if we run this policy (or program) for a while until it executes a special interrupt action, will the internal storage cell number 15 contain the value 5, or not? Again there are two learning, reward-maximizing adversaries playing a zero sum game, occasionally betting on different yes/no outcomes of such computational experiments. The winner of such a bet gets a reward of 1, the loser -1. So each adversary is motivated to come up with questions whose answers surprise the other. And both are motivated to avoid seemingly trivial questions where both already agree on the outcome, or seemingly hard questions that none of them can reliably answer for now. Experiments showed that this type of curiosity may also accelerate the intake of external reward.[AC97][AC02]

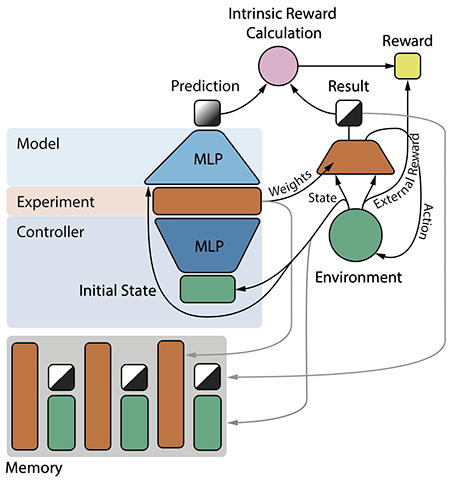
Learning One Abstract Bit at a Time Through Self-Invented Experiments Encoded as Neural Networks
4a. 2022: Complex experiments with binary outcomes encoded as NN weight matrices created by NN experiment generators

In more recent work,[AC22b] we re-implemented the curiosity principles of Sec. 4 (1997)[AC97][AC99][AC02] through neural, gradient-based Fast Weight Programmers dating back to 1991.[FWP0-1][FWP]

Here one NN (the controller C) generates the program or weight matrix[AC90] for another (R)NN called E which runs the experiment in an environment until it halts—E has a special halt neuron[SLIM] for that. A world model NN called M predicts the experiment's binary final outcome represented by the final activation of a special hidden result neuron in E. After the experiment, C's intrinsic reward is proportional to M's surprise or information gain (see Sec. 3). In general, each time step costs a small negative reward such that C is based towards generating simple and fast (but still surprising) experiments.

Like the 1997 system of Sec. 4, the neural 2022 system[AC22b] can learn to ask arbitrary, complex questions with computable answers. It can invent predictable abstractions of complex spatio-temporal event streams, while ignoring unpredictable details. Experiments that do not involve any interactions with the environment are called pure thought experiments. Initially interesting experiments become boring over time.[AC22b]

5. 2006: Maximizing compression progress like scientists and artists do

Femme Fractale: Lady in Red - Low-Complexity Art by Juergen Schmidhuber I have frequently pointed out that the history of science is a history of data compression progress through incremental discovery of simple laws that govern seemingly complex observation sequences.[AC06][AC09][AC10] How to implement this principle in an artificial scientist based on a controller C and a predictive world model M? Well, the better the predictions of M, the fewer bits are required to encode the history H of sensory input observations, because short codes can be used for inputs that M considers highly probable.[HUF] That is, the learning progress of the M in the probabilistic inference machine of Sec. 3 above[AC95] has a lot to do with the concept of compression progress. [AC06][AC09][AC10] However, it's not quite the same thing. In particular, it does not take into account the bits of information needed to specify M and its re-trained version M*. A more general approach is based on algorithmic information theory.[SOL][KOL][WA68][WA87][LIV][ALL2] Here C's intrinsic reward is indeed based on algorithmic compression progress.[AC06][AC09][AC10] Let us consider the history H up to the current input Q. We introduce some coding scheme for the weights of the model network M.[FM][KO0-2][CO1-4] And also a coding scheme for the history of all observations so far, given M.[HUF][WA68][RIS][FM][AC06] (For example, already in 1991, my first very deep learner based on unsupervised pre-training used hierarchical predictive coding to find compact internal representations of sequential data to facilitate downstream learning.[UN][UN0-2]) Now I(M) bits are needed to describe H without ignoring the costs of the weights of M, and I(M*) bits are necessary to describe H without ignoring the costs of the weights of M*. Then C's total current curiosity reward or intrinsic joy or fun reflects M's depth of insight, namely, the compression progress I(M)-I(M*) after having observed Q.[AC06][AC09][AC10]

How can we measure or at least approximate the above-mentioned information-theoretic costs of M and M*? Over the decades we have published several ways of learning to encode numerous weights of large NNs through very compact codes.[FM][KO0-2][CO1-4] Here we exploited that the Kolmogorov complexity or algorithmic information content of successful huge NNs may actually be rather small. For example, in July 2013, the compact codes of "Compressed Network Search"[CO2] yielded the first deep learning model to successfully learn control policies directly from high-dimensional sensory input (video) using RL (in this case RL through neuroevolution), without any unsupervised pre-training.

Read here how my Formal Theory of Fun uses the concept of compression progress to explain not only science but also art, music, and humor.[AC06][AC09][AC10] Take humor for example. Consider the following statement: Biological organisms are driven by the "Four Big F's": Feeding, Fighting, Fleeing, Mating. Some subjective observers who read this for the first time think it is funny. Why? As the eyes are sequentially scanning the text the brain receives a complex visual input stream. The latter is subjectively partially compressible as it relates to the observer's previous knowledge about letters and words. That is, given the reader's current knowledge and current compressor, the raw data can be encoded by fewer bits than required to store random data of the same size. But the punch line after the last comma is unexpected for those who expected another "F." Initially this failed expectation results in sub-optimal data compression—storage of expected events does not cost anything, but deviations from predictions require extra bits to encode them. The compressor, however, does not stay the same forever: within a short time interval, its learning algorithm kicks in and improves its performance on the data seen so far, by discovering the non-random, non-arbitrary and therefore compressible pattern relating the punch line to previous text and previous elaborate predictive knowledge about the "Four Big F's." This saves a few bits of storage. The number of saved bits (or a similar measure of learning progress) becomes the observer's intrinsic reward, possibly strong enough to motivate her to read on in search for more reward through additional yet unknown patterns. While previous attempts at explaining humor also focused on the element of surprise,[RAS85] they lacked the essential concept of novel pattern detection measured by compression progress due to learning.[AC06][AC09][AC10] This progress is zero whenever the unexpected is just random white noise, and thus no fun at all. Applications of my simple theory of humor can be found in this old youtube video of a talk on this subject which I gave at the Singularity Summit 2009 in NYC.

6. Does curiosity distort the basic RL problem?

The controller/model systems above (aka CM systems[PLAN4][PLAN]) typically maximize the sum of standard external rewards (for achieving user-given goals) and intrinsic curiosity rewards. Does this distort the basic RL problem? It turns out not so much. Unlike the external reward for eating three times a day, the curiosity reward in the systems above is ephemeral, because once something is known, there is no additional intrinsic reward for discovering it again.[AC10] That is, the external reward tends to dominate the total reward. In totally learnable environments, in the long run, the intrinsic reward even vanishes next to the external reward.[AC10] Which is nice, because in most RL applications we care only for the external reward.

7. Connections to metalearning since 1990

Metalearning or Learning to Learn Since 1987. Juergen Schmidhuber. The Section A Connection to Meta-Learning in the 1990 paper[AC90] already pointed out: "A model network can be used not only for predicting the controller's inputs but also for predicting its future outputs. A perfect model of this kind would model the internal changes of the control network. It would predict the evolution of the controller, and thereby the effects of the gradient descent procedure itself. In this case, the flow of activation in the model network would model the weight changes of the control network. This in turn comes close to the notion of learning how to learn." The paper[AC90] also introduced planning with recurrent NNs (RNNs) as world models,[PLAN] and high-dimensional reward signals. Unlike in traditional RL, those reward signals were also used as informative inputs to the controller NN learning to execute actions that maximise cumulative reward.[MIR](Sec. 13)[DEC](Sec. 5) This is important for metalearning: an NN that cannot see its own errors or rewards cannot learn a better way of using such signals as inputs for self-invented learning algorithms.

A few years later, I combined Meta-RL and Adversarial Artificial Curiosity in the system of Sec. 4.[AC97,AC99,AC02][META](Sec. 6)

8. 2011: PowerPlay continually searches for novel formally well-defined computational problems whose solutions can easily be added to the skill repertoire, taking into account verification time

PowerPlay: training an increasingly general problem solver by continually searching for the simplest still unsolvable problem My curious reinforcement learning Q&A systems of the 1990s did not explicitly, formally enumerate their questions. But the more recent PowerPlay framework (2011)[PP][PPa][PP1] does. Let us step back for a moment. What is the set of all formalisable questions that any curious system could possibly ask? How to decide whether a given question has been answered by a learning machine? To define a question, we need a computational procedure that takes a solution candidate (possibly proposed by a policy) and decides whether it is an answer to the question or not. PowerPlay essentially enumerates the set of all such procedures (or some user-defined subset thereof), thus enumerating all possible questions or problems (including environments in which problems are to be solved). It searches for the simplest question that the current policy cannot yet answer but can quickly learn to answer without forgetting the answers to previously answered questions. The computational costs of verifying that nothing has been forgotten are taken into account. What is the simplest such Q&A to be added to the repertoire? It is the cheapest one—the one that is found first. Then the next trial starts, where new Q&As may build on previous Q&As. Compare also the One Big Net For Everything[PLAN5] which offers a simplified, less strict NN version of PowerPlay. Also see the work from 2015 on RL robots learning to explore using high-dimensional video inputs and PowerPlay-like intrinsic motivation.[PP2]

The PowerPlay paper (2011-13)[PP] starts as follows: "Most of computer science focuses on automatically solving given computational problems. I focus on automatically inventing or discovering problems in a way inspired by the playful behavior of animals and humans, to train a more and more general problem solver from scratch in an unsupervised fashion." PowerPlay can use the metalearning OOPS[OOPS1-3][META](Sec. 4) to continually invent on its own new goals and tasks, incrementally learning to become a more and more general problem solver in an active, partially unsupervised or self-supervised fashion.

9. 2015: Planning and curiosity with spatio-temporal abstractions in NNs

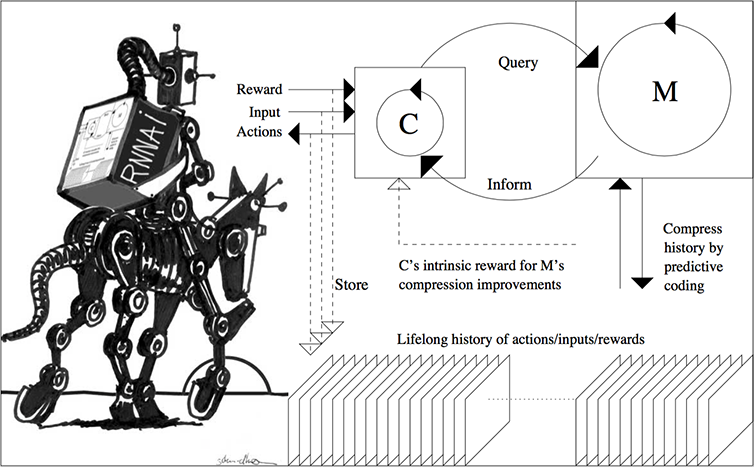
Learning to think

The recurrent controller/world model system of 1990[AC90] focused on naive "millisecond by millisecond planning," trying to predict and plan every little detail of its possible futures.[PLAN] Even today, this is still a standard approach in many RL applications, e.g., RL for board games such as Chess and Go. My more recent work of 2015, however, has focused on abstract (e.g., hierarchical) planning and reasoning,[PLAN4-5][PLAN][LEC] continuing the work of 1997[AC97][AC02] summarized in Sec. 4 above, and early work on hierarchical RL since 1991.[HRL0-5][MIR](Sec. 10)[DLH]

Guided by algorithmic information theory, I described recurrent NN-based AIs (RNNAIs) that can be trained on never-ending sequences of tasks, some of them provided by the user, others invented by the RNNAI itself in a curious, playful fashion, to improve its RNN-based world model. Unlike the system of 1990,[AC90] the RNNAI[PLAN4] learns to actively query its model for abstract reasoning and planning and decision making, essentially learning to think.[PLAN4] Compare also our recent related work on learning (hierarchically) structured concept spaces based on abstract objects.[OBJ2-5] The previous ideas[PLAN4-5] can be applied to many other cases where one RNN-like system exploits the algorithmic information content of another. They also explain concepts such as mirror neurons.[PLAN4] See also recent work with David Ha of Google (2018):[PLAN6] a world model that extracts compressed spatio-temporal representations which are fed into compact and simple policies trained by evolution, achieving state of the art results in various environments.

Agents with adaptive recurrent world models even suggest a simple explanation of consciousness and self-awareness dating back three decades.[PLAN][UN][CON16][CATCH]

Acknowledgments

Thanks to several expert reviewers for useful comments. Since science is about self-correction, let me know under juergen@idsia.ch if you can spot any remaining error. There is another version of this article with references in plain text style. The contents of this article may be used for educational and non-commercial purposes, including articles for Wikipedia and similar sites. This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

References

[AC] J.  Schmidhuber (AI Blog, 2021, updated 2023). 3 decades of artificial curiosity & creativity. Our artificial scientists not only answer given questions but also invent new questions. They achieve curiosity through: (1990) the principle of generative adversarial networks, (1991) neural nets that maximise learning progress, (1995) neural nets that maximise information gain (optimally since 2011), (1997-2022) adversarial design of surprising computational experiments, (2006) maximizing compression progress like scientists/artists/comedians do, (2011) PowerPlay... Since 2012: applications to real robots.

[AC90] J.  Schmidhuber. Making the world differentiable: On using fully recurrent self-supervised neural networks for dynamic reinforcement learning and planning in non-stationary environments. Technical Report FKI-126-90, TUM, Feb 1990, revised Nov 1990. PDF. The first paper on planning with reinforcement learning recurrent neural networks (NNs) (more) and on generative adversarial networks where a generator NN is fighting a predictor NN in a minimax game (more).

[AC90b] J.  Schmidhuber. A possibility for implementing curiosity and boredom in model-building neural controllers. In J. A. Meyer and S. W. Wilson, editors, Proc. of the International Conference on Simulation of Adaptive Behavior: From Animals to Animats, pages 222-227. MIT Press/Bradford Books, 1991. PDF. More.

[AC91] J. Schmidhuber. Adaptive confidence and adaptive curiosity. Technical Report FKI-149-91, Inst. f. Informatik, Tech. Univ. Munich, April 1991. PDF.

[AC91b] J.  Schmidhuber. Curious model-building control systems. In Proc. International Joint Conference on Neural Networks, Singapore, volume 2, pages 1458-1463. IEEE, 1991. PDF.

[AC95] J. Storck, S. Hochreiter, and J. Schmidhuber. Reinforcement-driven information acquisition in non-deterministic environments. In Proc. ICANN'95, vol. 2, pages 159-164. EC2 & CIE, Paris, 1995. PDF.

[AC97] J. Schmidhuber. What's interesting? Technical Report IDSIA-35-97, IDSIA, July 1997. Focus on automatic creation of predictable internal abstractions of complex spatio-temporal events: two competing, intrinsically motivated agents agree on essentially arbitrary algorithmic experiments and bet on their possibly surprising (not yet predictable) outcomes in zero-sum games, each agent potentially profiting from outwitting / surprising the other by inventing experimental protocols where both modules disagree on the predicted outcome. The focus is on exploring the space of general algorithms (as opposed to traditional simple mappings from inputs to outputs); the general system focuses on the interesting things by losing interest in both predictable and unpredictable aspects of the world. Unlike our previous systems with intrinsic motivation,[AC90-AC95] the system also takes into account the computational cost of learning new skills, learning when to learn and what to learn. See later publications.[AC99][AC02]

[AC98] M. Wiering and J. Schmidhuber. Efficient model-based exploration. In R. Pfeiffer, B. Blumberg, J. Meyer, S. W. Wilson, eds., From Animals to Animats 5: Proceedings of the Fifth International Conference on Simulation of Adaptive Behavior, p. 223-228, MIT Press, 1998.

[AC98b] M. Wiering and J. Schmidhuber. Learning exploration policies with models. In Proc. CONALD, 1998.

[AC99] J. Schmidhuber. Artificial Curiosity Based on Discovering Novel Algorithmic Predictability Through Coevolution. In P. Angeline, Z. Michalewicz, M. Schoenauer, X. Yao, Z. Zalzala, eds., Congress on Evolutionary Computation, p. 1612-1618, IEEE Press, Piscataway, NJ, 1999.

[AC02] J. Schmidhuber. Exploring the Predictable. In Ghosh, S. Tsutsui, eds., Advances in Evolutionary Computing, p. 579-612, Springer, 2002. PDF.

[AC05] J.  Schmidhuber. Self-Motivated Development Through Rewards for Predictor Errors / Improvements. Developmental Robotics 2005 AAAI Spring Symposium, March 21-23, 2005, Stanford University, CA. PDF.

[AC06] J.  Schmidhuber. Developmental Robotics, Optimal Artificial Curiosity, Creativity, Music, and the Fine Arts. Connection Science, 18(2): 173-187, 2006. PDF.

[AC07] J. Schmidhuber. Simple Algorithmic Principles of Discovery, Subjective Beauty, Selective Attention, Curiosity & Creativity. In V. Corruble, M. Takeda, E. Suzuki, eds., Proc. 10th Intl. Conf. on Discovery Science (DS 2007) p. 26-38, LNAI 4755, Springer, 2007. Also in M. Hutter, R. A. Servedio, E. Takimoto, eds., Proc. 18th Intl. Conf. on Algorithmic Learning Theory (ALT 2007) p. 32, LNAI 4754, Springer, 2007. (Joint invited lecture for DS 2007 and ALT 2007, Sendai, Japan, 2007.) Preprint arxiv:0709.0674. PDF. Curiosity as the drive to improve the compression of the lifelong sensory input stream: interestingness as the first derivative of subjective "beauty" or compressibility.

[AC08] Driven by Compression Progress. In Proc. Knowledge-Based Intelligent Information and Engineering Systems KES-2008, Lecture Notes in Computer Science LNCS 5177, p 11, Springer, 2008. (Abstract of invited keynote talk.) PDF.

[AC09] J. Schmidhuber. Art & science as by-products of the search for novel patterns, or data compressible in unknown yet learnable ways. In M. Botta (ed.), Et al. Edizioni, 2009, pp. 98-112. PDF. (More on artificial scientists and artists.)

[AC09a] J. Schmidhuber. Driven by Compression Progress: A Simple Principle Explains Essential Aspects of Subjective Beauty, Novelty, Surprise, Interestingness, Attention, Curiosity, Creativity, Art, Science, Music, Jokes. Based on keynote talk for KES 2008 (below) and joint invited lecture for ALT 2007 / DS 2007 (below). Short version: ref 17 below. Long version in G. Pezzulo, M. V. Butz, O. Sigaud, G. Baldassarre, eds.: Anticipatory Behavior in Adaptive Learning Systems, from Sensorimotor to Higher-level Cognitive Capabilities, Springer, LNAI, 2009. Preprint (2008, revised 2009): arXiv:0812.4360. PDF (Dec 2008). PDF (April 2009).

[AC09b] J. Schmidhuber. Simple Algorithmic Theory of Subjective Beauty, Novelty, Surprise, Interestingness, Attention, Curiosity, Creativity, Art, Science, Music, Jokes. Journal of SICE, 48(1):21-32, 2009. PDF.

[AC10] J. Schmidhuber. Formal Theory of Creativity, Fun, and Intrinsic Motivation (1990-2010). IEEE Transactions on Autonomous Mental Development, 2(3):230-247, 2010. IEEE link. PDF.

[AC10a] J. Schmidhuber. Artificial Scientists & Artists Based on the Formal Theory of Creativity. In Proceedings of the Third Conference on Artificial General Intelligence (AGI-2010), Lugano, Switzerland. PDF.

[AC11] Sun Yi, F. Gomez, J. Schmidhuber. Planning to Be Surprised: Optimal Bayesian Exploration in Dynamic Environments. In Proc. Fourth Conference on Artificial General Intelligence (AGI-11), Google, Mountain View, California, 2011. PDF.

[AC11a] V. Graziano, T. Glasmachers, T. Schaul, L. Pape, G. Cuccu, J. Leitner, J. Schmidhuber. Artificial Curiosity for Autonomous Space Exploration. Acta Futura 4:41-51, 2011 (DOI: 10.2420/AF04.2011.41). PDF.

[AC11b] G. Cuccu, M. Luciw, J. Schmidhuber, F. Gomez. Intrinsically Motivated Evolutionary Search for Vision-Based Reinforcement Learning. In Proc. Joint IEEE International Conference on Development and Learning (ICDL) and on Epigenetic Robotics (ICDL-EpiRob 2011), Frankfurt, 2011. PDF.

[AC11c] M. Luciw, V. Graziano, M. Ring, J. Schmidhuber. Artificial Curiosity with Planning for Autonomous Visual and Perceptual Development. In Proc. Joint IEEE International Conference on Development and Learning (ICDL) and on Epigenetic Robotics (ICDL-EpiRob 2011), Frankfurt, 2011. PDF.

[AC11d] T. Schaul, L. Pape, T. Glasmachers, V. Graziano J. Schmidhuber. Coherence Progress: A Measure of Interestingness Based on Fixed Compressors. In Proc. Fourth Conference on Artificial General Intelligence (AGI-11), Google, Mountain View, California, 2011. PDF.

[AC11e] T. Schaul, Yi Sun, D. Wierstra, F. Gomez, J. Schmidhuber. Curiosity-Driven Optimization. IEEE Congress on Evolutionary Computation (CEC-2011), 2011. PDF.

[AC11f] H. Ngo, M. Ring, J. Schmidhuber. Curiosity Drive based on Compression Progress for Learning Environment Regularities. In Proc. Joint IEEE International Conference on Development and Learning (ICDL) and on Epigenetic Robotics (ICDL-EpiRob 2011), Frankfurt, 2011.

[AC12] L. Pape, C. M. Oddo, M. Controzzi, C. Cipriani, A. Foerster, M. C. Carrozza, J. Schmidhuber. Learning tactile skills through curious exploration. Frontiers in Neurorobotics 6:6, 2012, doi: 10.3389/fnbot.2012.00006

[AC12a] H. Ngo, M. Luciw, A. Foerster, J. Schmidhuber. Learning Skills from Play: Artificial Curiosity on a Katana Robot Arm. Proc. IJCNN 2012. PDF. Video.

[AC12b] V. R. Kompella, M. Luciw, M. Stollenga, L. Pape, J. Schmidhuber. Autonomous Learning of Abstractions using Curiosity-Driven Modular Incremental Slow Feature Analysis. Proc. IEEE Conference on Development and Learning / EpiRob 2012 (ICDL-EpiRob'12), San Diego, 2012.

[AC12c] J. Schmidhuber. Maximizing Fun By Creating Data With Easily Reducible Subjective Complexity. In G. Baldassarre and M. Mirolli (eds.), Roadmap for Intrinsically Motivated Learning. Springer, 2012.

[AC20] J. Schmidhuber. Generative Adversarial Networks are Special Cases of Artificial Curiosity (1990) and also Closely Related to Predictability Minimization (1991). Neural Networks, Volume 127, p 58-66, 2020. Preprint arXiv/1906.04493.

[AC22] A. Ramesh, L. Kirsch, S. van Steenkiste, J. Schmidhuber. Exploring through Random Curiosity with General Value Functions. Advances in Neural Information Processing Systems (NeurIPS), New Orleans, 2022. Preprint arXiv:2211.10282.

[AC22b] V. Herrmann, L. Kirsch, J. Schmidhuber Learning One Abstract Bit at a Time Through Self-Invented Experiments Encoded as Neural Networks. Preprint arXiv:2212.14374, 2022.

[ALL2] J. Schmidhuber (2000). Algorithmic theories of everything. ArXiv: quant-ph/ 0011122. See also: International Journal of Foundations of Computer Science 13(4):587-612, 2002: PDF. See also: Proc. COLT 2002: PDF. More.

[ATT] J. Schmidhuber (AI Blog, 2020). 30-year anniversary of end-to-end differentiable sequential neural attention. Plus goal-conditional reinforcement learning. We had both hard attention (1990) and soft attention (1991-93).[FWP] Today, both types are very popular.

[ATT0] J. Schmidhuber and R. Huber. Learning to generate focus trajectories for attentive vision. Technical Report FKI-128-90, Institut für Informatik, Technische Universität München, 1990. PDF.

[ATT1] J. Schmidhuber and R. Huber. Learning to generate artificial fovea trajectories for target detection. International Journal of Neural Systems, 2(1 & 2):135-141, 1991. Based on TR FKI-128-90, TUM, 1990. PDF. More.

[ATT2] J.  Schmidhuber. Learning algorithms for networks with internal and external feedback. In D. S. Touretzky, J. L. Elman, T. J. Sejnowski, and G. E. Hinton, editors, Proc. of the 1990 Connectionist Models Summer School, pages 52-61. San Mateo, CA: Morgan Kaufmann, 1990. PS. (PDF.)

[BUR18] Y. Burda, H. Edwards, D. Pathak, A. Storkey, T. Darrell, A. A. Efros. Large-scale study of curiosity-driven learning. Preprint arXiv:1808.04355, 2018.

[CATCH] J. Schmidhuber. Philosophers & Futurists, Catch Up! Response to The Singularity. Journal of Consciousness Studies, Volume 19, Numbers 1-2, pp. 173-182(10), 2012. PDF.

[CON16] J. Carmichael (2016). Artificial Intelligence Gained Consciousness in 1991. Why A.I. pioneer Jürgen Schmidhuber is convinced the ultimate breakthrough already happened. Inverse, 2016. Link.

[CO1] J. Koutnik, F. Gomez, J. Schmidhuber (2010). Evolving Neural Networks in Compressed Weight Space. Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2010), Portland, 2010. PDF.

[CO2] J. Koutnik, G. Cuccu, J. Schmidhuber, F. Gomez. Evolving Large-Scale Neural Networks for Vision-Based Reinforcement Learning. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), Amsterdam, July 2013. PDF.

[CO3] R. K. Srivastava, J. Schmidhuber, F. Gomez. Generalized Compressed Network Search. Proc. GECCO 2012. PDF.

[CO4] S. van Steenkiste, J. Koutnik, K. Driessens, J. Schmidhuber. A wavelet-based encoding for neuroevolution. Proceedings of the Genetic and Evolutionary Computation Conference 2016, GECCO'16, pages 517-524, New York, NY, USA, 2016. ACM.

[DEC] J. Schmidhuber (AI Blog, 02/20/2020, revised 2021). The 2010s: Our Decade of Deep Learning / Outlook on the 2020s. The recent decade's most important developments and industrial applications based on our AI, with an outlook on the 2020s, also addressing privacy and data markets.

[DL1] J. Schmidhuber, 2015. Deep Learning in neural networks: An overview. Neural Networks, 61, 85-117. More.

[DL2] J. Schmidhuber, 2015. Deep Learning. Scholarpedia, 10(11):32832.

[DL4] J. Schmidhuber (AI Blog, 2017). Our impact on the world's most valuable public companies: Apple, Google, Microsoft, Facebook, Amazon... By 2015-17, neural nets developed in my labs were on over 3 billion devices such as smartphones, and used many billions of times per day, consuming a significant fraction of the world's compute. Examples: greatly improved (CTC-based) speech recognition on all Android phones, greatly improved machine translation through Google Translate and Facebook (over 4 billion LSTM-based translations per day), Apple's Siri and Quicktype on all iPhones, the answers of Amazon's Alexa, etc. Google's 2019 on-device speech recognition (on the phone, not the server) is still based on LSTM.

[DLH] J. Schmidhuber (AI Blog, 2022). Annotated History of Modern AI and Deep Learning. Technical Report IDSIA-22-22, IDSIA, Lugano, Switzerland, 2022. Preprint arXiv:2212.11279.

[FED] V. V. Fedorov. Theory of optimal experiments. Academic Press, 1972.

[FM] S. Hochreiter and J. Schmidhuber. Flat minimum search finds simple nets. Technical Report FKI-200-94, Fakultät für Informatik, Technische Universität München, December 1994. PDF.

[FWP] J.  Schmidhuber (AI Blog, 26 March 2021, updated 2022). 26 March 1991: Neural nets learn to program neural nets with fast weights—like Transformer variants. 2021: New stuff! 30-year anniversary of a now popular alternative[FWP0-1] to recurrent NNs. A slow feedforward NN learns by gradient descent to program the changes of the fast weights[FAST,FASTa] of another NN, separating memory and control like in traditional computers. Such Fast Weight Programmers[FWP0-6,FWPMETA1-8] can learn to memorize past data, e.g., by computing fast weight changes through additive outer products of self-invented activation patterns[FWP0-1] (now often called keys and values for self-attention[TR1-6]). The similar Transformers[TR1-2] combine this with projections and softmax and are now widely used in natural language processing. For long input sequences, their efficiency was improved through Transformers with linearized self-attention[TR5-6] which are formally equivalent to Schmidhuber's 1991 outer product-based Fast Weight Programmers (apart from normalization). In 1993, he introduced the attention terminology[FWP2] now used in this context,[ATT] and extended the approach to RNNs that program themselves. See tweet of 2022.

[FWP0] J.  Schmidhuber. Learning to control fast-weight memories: An alternative to recurrent nets. Technical Report FKI-147-91, Institut für Informatik, Technische Universität München, 26 March 1991. PDF. First paper on fast weight programmers that separate storage and control: a slow net learns by gradient descent to compute weight changes of a fast net. The outer product-based version (Eq. 5) is now known as a "Transformer with linearized self-attention" (apart from normalization).[FWP]

[FWP1] J. Schmidhuber. Learning to control fast-weight memories: An alternative to recurrent nets. Neural Computation, 4(1):131-139, 1992. Based on [FWP0]. PDF. HTML. Pictures (German). See tweet of 2022 for 30-year anniversary.

[FWP2] J. Schmidhuber. Reducing the ratio between learning complexity and number of time-varying variables in fully recurrent nets. In Proceedings of the International Conference on Artificial Neural Networks, Amsterdam, pages 460-463. Springer, 1993. PDF. First recurrent NN-based fast weight programmer using outer products, introducing the terminology of learning "internal spotlights of attention."

[FWP6] I. Schlag, K. Irie, J. Schmidhuber. Linear Transformers Are Secretly Fast Weight Memory Systems. 2021. Preprint arXiv:2102.11174.

[H90] W. D. Hillis. Co-evolving parasites improve simulated evolution as an optimization procedure. Physica D: Nonlinear Phenomena, 42(1-3):228-234, 1990.

[HRL0] J.  Schmidhuber. Towards compositional learning with dynamic neural networks. Technical Report FKI-129-90, Institut für Informatik, Technische Universität München, 1990. PDF.

[HRL0] J.  Schmidhuber. Towards compositional learning with dynamic neural networks. Technical Report FKI-129-90, Institut für Informatik, Technische Universität München, 1990. PDF. An RL machine gets extra command inputs of the form (start, goal). An evaluator NN learns to predict the current rewards/costs of going from start to goal. An (R)NN-based subgoal generator also sees (start, goal), and uses (copies of) the evaluator NN to learn by gradient descent a sequence of cost-minimising intermediate subgoals. The RL machine tries to use such subgoal sequences to achieve final goals. The system is learning action plans at multiple levels of abstraction and multiple time scales and solves what Y. LeCun called an "open problem" in 2022.[LEC]

[HRL1] J. Schmidhuber. Learning to generate sub-goals for action sequences. In T. Kohonen, K. Mäkisara, O. Simula, and J. Kangas, editors, Artificial Neural Networks, pages 967-972. Elsevier Science Publishers B.V., North-Holland, 1991. PDF. Extending TR FKI-129-90, TUM, 1990.

[HRL4] M. Wiering and J. Schmidhuber. HQ-Learning. Adaptive Behavior 6(2):219-246, 1997. PDF.

[HRL5] J. Schmidhuber. Subgoal learning & hierarchical reinforcement learning since 1990. (More.)

[HUF] D. A. Huffman. A method for construction of minimum-redundancy codes. Proceedings IRE, 40:1098-1101, 1952.

[ITT5] L. Itti, P. F. Baldi. Bayesian surprise attracts human attention. In Advances in Neural Information Processing Systems (NIPS) 19, pages 547-554. MIT Press, Cambridge, MA, 2005.

[KUL] S. Kullback and R. A. Leibler. On information and sufficiency. The Annals of Mathematical Statistics, pages 79-86, 1951.

[KO0] J.  Schmidhuber. Discovering problem solutions with low Kolmogorov complexity and high generalization capability. Technical Report FKI-194-94, Fakultät für Informatik, Technische Universität München, 1994. PDF.

[KO1] J.  Schmidhuber. Discovering solutions with low Kolmogorov complexity and high generalization capability. In A. Prieditis and S. Russell, editors, Machine Learning: Proceedings of the Twelfth International Conference (ICML 1995), pages 488-496. Morgan Kaufmann Publishers, San Francisco, CA, 1995. PDF.

[KO2] J. Schmidhuber. Discovering neural nets with low Kolmogorov complexity and high generalization capability. Neural Networks, 10(5):857-873, 1997. PDF.

[KOL] A. N. Kolmogorov. Three approaches to the quantitative definition of information. Problems of Information Transmission, 1:1-11, 1965.

[LEC] J. Schmidhuber (AI Blog, 2022). LeCun's 2022 paper on autonomous machine intelligence rehashes but does not cite essential work of 1990-2015. Years ago, Schmidhuber's team published most of what Y. LeCun calls his "main original contributions:" neural nets that learn multiple time scales and levels of abstraction, generate subgoals, use intrinsic motivation to improve world models, and plan (1990); controllers that learn informative predictable representations (1997), etc. This was also discussed on Hacker News, reddit, and in the media. See tweet1. LeCun also listed the "5 best ideas 2012-2022" without mentioning that most of them are from Schmidhuber's lab, and older. See tweet2.

[LIV] M. Li and P. M. B. Vitanyi. An Introduction to Kolmogorov Complexity and its Applications (2nd edition). Springer, 1997.

[META] J. Schmidhuber (AI Blog, 2020). 1/3 century anniversary of first publication on metalearning machines that learn to learn (1987). For its cover I drew a robot that bootstraps itself. 1992-: gradient descent-based neural metalearning. 1994-: Meta-Reinforcement Learning with self-modifying policies. 1997: Meta-RL plus artificial curiosity and intrinsic motivation. 2002-: asymptotically optimal metalearning for curriculum learning. 2003-: mathematically optimal Gödel Machine. 2020: new stuff!

[MIR] J. Schmidhuber (AI Blog, Oct 2019, updated 2021, 2022). Deep Learning: Our Miraculous Year 1990-1991. Preprint arXiv:2005.05744, 2020. The deep learning neural networks of Schmidhuber's team have revolutionised pattern recognition and machine learning, and are now heavily used in academia and industry. In 2020-21, we celebrate that many of the basic ideas behind this revolution were published within fewer than 12 months in the "Annus Mirabilis" 1990-1991 at TU Munich.

[MOST] J.  Schmidhuber (AI Blog, 2021). The most cited neural networks all build on work done in my labs. Foundations of the most popular NNs originated in my labs at TU Munich and IDSIA. Here I mention: (1) Long Short-Term Memory (LSTM), (2) ResNet (which is our earlier Highway Net with open gates), (3) AlexNet and VGG Net (both building on our similar earlier DanNet: the first deep convolutional NN to win image recognition competitions), (4) Generative Adversarial Networks (an instance of my earlier Adversarial Artificial Curiosity), and (5) variants of Transformers (Transformers with linearized self-attention are formally equivalent to my earlier Fast Weight Programmers). Most of this started with our Annus Mirabilis of 1990-1991.[MIR]

[OBJ1] K. Greff, A. Rasmus, M. Berglund, T. Hao, H. Valpola, J. Schmidhuber (2016). Tagger: Deep unsupervised perceptual grouping. NIPS 2016, pp. 4484-4492.

[OBJ2] K. Greff, S. van Steenkiste, J. Schmidhuber (2017). Neural expectation maximization. NIPS 2017, pp. 6691-6701.

[OBJ3] S. van Steenkiste, M. Chang, K. Greff, J. Schmidhuber (2018). Relational neural expectation maximization: Unsupervised discovery of objects and their interactions. ICLR 2018.

[OBJ4] A. Stanic, S. van Steenkiste, J. Schmidhuber (2021). Hierarchical Relational Inference. AAAI 2021.

[OBJ5] A. Gopalakrishnan, S. van Steenkiste, J. Schmidhuber (2020). Unsupervised Object Keypoint Learning using Local Spatial Predictability. In Proc. ICLR 2021. Preprint arXiv/2011.12930.

[OOPS1] J. Schmidhuber. Bias-Optimal Incremental Problem Solving. In S. Becker, S. Thrun, K. Obermayer, eds., Advances in Neural Information Processing Systems 15, N(eur)IPS'15, MIT Press, Cambridge MA, p. 1571-1578, 2003. PDF

[OOPS2] J. Schmidhuber. Optimal Ordered Problem Solver. Machine Learning, 54, 211-254, 2004. PDF. HTML. HTML overview. Download OOPS source code in crystalline format.

[OOPS3] Schmidhuber, J., Zhumatiy, V. and Gagliolo, M. Bias-Optimal Incremental Learning of Control Sequences for Virtual Robots. In Groen, F., Amato, N., Bonarini, A., Yoshida, E., and Kroese, B., editors: Proceedings of the 8-th conference on Intelligent Autonomous Systems, IAS-8, Amsterdam, The Netherlands, pp. 658-665, 2004. PDF.

[OUD13] P.-Y. Oudeyer, A. Baranes, F. Kaplan. Intrinsically motivated learning of real world sensorimotor skills with developmental constraints. In G. Baldassarre and M. Mirolli, editors, Intrinsically Motivated Learning in Natural and Artificial Systems. Springer, 2013.

[PAT17] D. Pathak, P. Agrawal, A. A. Efros, T. Darrell. Curiosity-driven exploration by self-supervised prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, pages 16-17, 2017.

[PHD] J.  Schmidhuber. Dynamische neuronale Netze und das fundamentale raumzeitliche Lernproblem (Dynamic neural nets and the fundamental spatio-temporal credit assignment problem). Dissertation, Institut für Informatik, Technische Universität München, 1990. PDF. HTML.

[PLAN] J. Schmidhuber (AI Blog, 2020). 30-year anniversary of planning & reinforcement learning with recurrent world models and artificial curiosity (1990). This work also introduced high-dimensional reward signals, deterministic policy gradients for RNNs, the GAN principle (widely used today). Agents with adaptive recurrent world models even suggest a simple explanation of consciousness & self-awareness.

[PLAN2] J.  Schmidhuber. An on-line algorithm for dynamic reinforcement learning and planning in reactive environments. In Proc. IEEE/INNS International Joint Conference on Neural Networks, San Diego, volume 2, pages 253-258, June 17-21, 1990. Based on [AC90].

[PLAN3] J.  Schmidhuber. Reinforcement learning in Markovian and non-Markovian environments. In R. P. Lippman, J. E. Moody, and D. S. Touretzky, editors, Advances in Neural Information Processing Systems 3, NIPS'3, pages 500-506. San Mateo, CA: Morgan Kaufmann, 1991. PDF. Partially based on [AC90].

[PLAN4] J. Schmidhuber. On Learning to Think: Algorithmic Information Theory for Novel Combinations of Reinforcement Learning Controllers and Recurrent Neural World Models. Report arXiv:1210.0118 [cs.AI], 2015.

[PLAN5] One Big Net For Everything. Preprint arXiv:1802.08864 [cs.AI], Feb 2018.

[PLAN6] D. Ha, J. Schmidhuber. Recurrent World Models Facilitate Policy Evolution. Advances in Neural Information Processing Systems (NIPS), Montreal, 2018. (Talk.) Preprint arXiv:1809.01999. Github: World Models.

[PM0] J. Schmidhuber. Learning factorial codes by predictability minimization. TR CU-CS-565-91, Univ. Colorado at Boulder, 1991. PDF. More.

[PM1] J. Schmidhuber. Learning factorial codes by predictability minimization. Neural Computation, 4(6):863-879, 1992. PDF. More.

[PM2] J. Schmidhuber, M. Eldracher, B. Foltin. Semilinear predictability minimzation produces well-known feature detectors. Neural Computation, 8(4):773-786, 1996. PDF. More.

[PP] J. Schmidhuber. POWERPLAY: Training an Increasingly General Problem Solver by Continually Searching for the Simplest Still Unsolvable Problem. Frontiers in Cognitive Science, 2013. ArXiv preprint (2011): arXiv:1112.5309 [cs.AI]

[PPa] R. K. Srivastava, B. R. Steunebrink, M. Stollenga, J. Schmidhuber. Continually Adding Self-Invented Problems to the Repertoire: First Experiments with POWERPLAY. Proc. IEEE Conference on Development and Learning / EpiRob 2012 (ICDL-EpiRob'12), San Diego, 2012. PDF.

[PP1] R. K. Srivastava, B. Steunebrink, J. Schmidhuber. First Experiments with PowerPlay. Neural Networks, 2013. ArXiv preprint (2012): arXiv:1210.8385 [cs.AI].

[PP2] V. Kompella, M. Stollenga, M. Luciw, J. Schmidhuber. Continual curiosity-driven skill acquisition from high-dimensional video inputs for humanoid robots. Artificial Intelligence, 2015.

[R2] Reddit/ML, 2019. J. Schmidhuber really had GANs in 1990.

[RAS85] V. Raskin (1985). Semantic Mechanisms of Humor. Dordrecht & Boston & Lancaster, 1985.

[RES5] Gloye, A., Wiesel, F., Tenchio, O., Simon, M. Reinforcing the Driving Quality of Soccer Playing Robots by Anticipation, IT - Information Technology, vol. 47, nr. 5, Oldenbourg Wissenschaftsverlag, 2005. PDF.

[RES7] J. Schmidhuber: Prototype resilient, self-modeling robots. Correspondence, Science, 316, no. 5825 p 688, May 2007.

[RIS] J. Rissanen. Modeling by shortest data description. Automatica, 14:465-471, 1978.

[S59] A. L. Samuel. Some studies in machine learning using the game of checkers. IBM Journal on Research and Development, 3:210-229, 1959.

[SHA] C. E. Shannon. A mathematical theory of communication (parts I and II). Bell System Technical Journal, XXVII:379-423, 1948.

[SIN5] S. Singh, A. G. Barto, N. Chentanez. Intrinsically motivated reinforcement learning. In Advances in Neural Information Processing Systems 17 (NIPS). MIT Press, Cambridge, MA, 2005.

[SLIM] J. Schmidhuber. Self-Delimiting Neural Networks. Preprint arxiv:1210.0118, 2012.

[SNT] J. Schmidhuber, S. Heil (1996). Sequential neural text compression. IEEE Trans. Neural Networks, 1996. PDF. A probabilistic language model based on predictive coding; an earlier version appeared at NIPS 1995.

[SOL] R. J. Solomonoff. A formal theory of inductive inference. Part I. Information and Control, 7:1-22, 1964.

[T22] J. Schmidhuber (AI Blog, 2022). Scientific Integrity and the History of Deep Learning: The 2021 Turing Lecture, and the 2018 Turing Award. Technical Report IDSIA-77-21, IDSIA, Lugano, Switzerland, 2022.

[UN] J. Schmidhuber (AI Blog, 2021). 30-year anniversary. 1991: First very deep learning with unsupervised or self-supervised pre-training. Unsupervised hierarchical predictive coding (with self-supervised target generation) finds compact internal representations of sequential data to facilitate downstream deep learning. The hierarchy can be distilled into a single deep neural network (suggesting a simple model of conscious and subconscious information processing). 1993: solving problems of depth >1000.

[UN0] J.  Schmidhuber. Neural sequence chunkers. Technical Report FKI-148-91, Institut für Informatik, Technische Universität München, April 1991. PDF. Unsupervised/self-supervised learning and predictive coding is used in a deep hierarchy of recurrent neural networks (RNNs) to find compact internal representations of long sequences of data, across multiple time scales and levels of abstraction. Each RNN tries to solve the pretext task of predicting its next input, sending only unexpected inputs to the next RNN above. The resulting compressed sequence representations greatly facilitate downstream supervised deep learning such as sequence classification. By 1993, the approach solved problems of depth 1000 [UN2] (requiring 1000 subsequent computational stages/layers—the more such stages, the deeper the learning). A variant collapses the hierarchy into a single deep net. It uses a so-called conscious chunker RNN which attends to unexpected events that surprise a lower-level so-called subconscious automatiser RNN. The chunker learns to understand the surprising events by predicting them. The automatiser uses a neural knowledge distillation procedure to compress and absorb the formerly conscious insights and behaviours of the chunker, thus making them subconscious. The systems of 1991 allowed for much deeper learning than previous methods. More.

[UN1] J. Schmidhuber. Learning complex, extended sequences using the principle of history compression. Neural Computation, 4(2):234-242, 1992. Based on TR FKI-148-91, TUM, 1991.[UN0] PDF. First working Deep Learner based on a deep RNN hierarchy (with different self-organising time scales), overcoming the vanishing gradient problem through unsupervised pre-training and predictive coding (with self-supervised target generation). Also: compressing or distilling a teacher net (the chunker) into a student net (the automatizer) that does not forget its old skills—such approaches are now widely used. More.

[UN2] J. Schmidhuber. Habilitation thesis, TUM, 1993. PDF. An ancient experiment on "Very Deep Learning" with credit assignment across 1200 time steps or virtual layers and unsupervised / self-supervised pre-training for a stack of recurrent NN can be found here (depth > 1000).

[UN3] J.  Schmidhuber, M. C. Mozer, and D. Prelinger. Continuous history compression. In H. Hüning, S. Neuhauser, M. Raus, and W. Ritschel, editors, Proc. of Intl. Workshop on Neural Networks, RWTH Aachen, pages 87-95. Augustinus, 1993.

[WA68] C. S. Wallace and D. M. Boulton. An information theoretic measure for classification. Computer Journal, 11(2):185-194, 1968.

[WA87] C. S. Wallace and P. R. Freeman. Estimation and inference by compact coding. Journal of the Royal Statistical Society, Series "B", 49(3):240-265, 1987.

.

Our impact on the world's most valuable public companies (Google, Apple, Microsoft, Facebook, mazon etc)