Abstract.
For over three decades I have published work about artificial scientists equipped with artificial curiosity and creativity, e.g.,
[AC90-AC20] [PP-PP2].
In this context,
I have frequently pointed out that there are two important things in science:
(A) Finding answers to given questions, and (B) Coming up with good questions.
(A) is arguably just the standard problem of computer science. But
how to implement the creative part (B) in artificial systems through
reinforcement learning (RL),
gradient-based artificial neural networks (NNs),
and other machine learning methods?
Here I summarise some of our approaches:
Sec. 1. 1990: Curiosity through the principle of generative adversarial networks
Sec. 2. 1991: Curiosity through NNs that maximise learning progress
Sec. 3. 1995: RL to maximise information gain or Bayesian surprise. (2011: Do this optimally)
Sec. 4. 1997: Adversarial RL agents design surprising computational experiments
Sec. 5. 2006: RL to maximise compression progress like scientists/artists/comedians do
Sec. 6. Does curiosity distort the basic reinforcement learning problem?
Sec. 7. Connections to metalearning since 1990
Sec. 8. 2011: PowerPlay continually searches for novel well-defined computational problems whose solutions can easily be added to the skill repertoire, taking into account verification time
Sec. 9. 2015: Planning and curiosity with spatio-temporal abstractions in NNs
1. 1990: Curiosity through the principle of generative adversarial networks
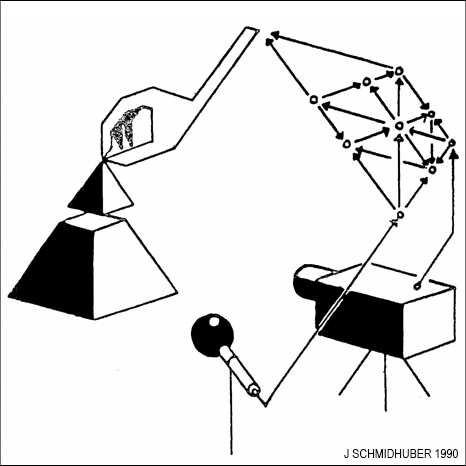
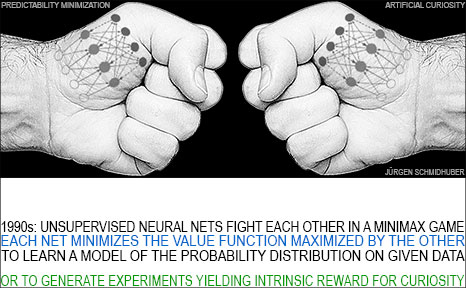 My first artificial Q&A system designed to invent and answer questions was the intrinsic motivation-based adversarial system from 1990 [AC90] [AC90b]. It employs two artificial neural networks (NNs) that duel each other. The first NN is the controller C. C probabilistically generates outputs that may influence an environment. The second NN is the world model M. It predicts the environmental reactions to C's outputs. Using gradient descent, M minimizes its error, thus becoming a better predictor. But in a zero sum game, the reward-maximizing C tries to find sequences of output actions that maximize the error of M. Thus M's loss is C's gain.
My first artificial Q&A system designed to invent and answer questions was the intrinsic motivation-based adversarial system from 1990 [AC90] [AC90b]. It employs two artificial neural networks (NNs) that duel each other. The first NN is the controller C. C probabilistically generates outputs that may influence an environment. The second NN is the world model M. It predicts the environmental reactions to C's outputs. Using gradient descent, M minimizes its error, thus becoming a better predictor. But in a zero sum game, the reward-maximizing C tries to find sequences of output actions that maximize the error of M. Thus M's loss is C's gain.
So C is asking questions through its action sequences, e.g., "what happens if I do this?", and M is learning to answer those questions.
Here C is motivated to come up with questions where M does not yet know the answer, and C loses interest in questions with known answers.
This was the start of a long series of papers on artificial curiosity and artificial scientists, e.g., [AC90-AC20] [PP-PP2].
Note that
instead of predicting the raw data, M may predict compressed versions thereof [PLAN4].
Generally speaking, a curious system may predict abstract internal representations [AC97][AC02] of raw data (Sec. 4).
 Not only the 1990s but also more recent years saw successful
applications of this simple adversarial principle and its variants in
Reinforcement Learning (RL) settings, e.g.,
[SIN5]
[OUD13]
[PAT17]
[BUR18].
Q&As help to understand the world
which is necessary for planning
[PLAN] [PLAN2-6] [RES5-7]
and may boost external reward
[AC91] [AC97] [AC02] [PAT17]
[BUR18].
In the 2010s, the concepts of 1990
became popular as
compute became cheaper [DEC].
Not only the 1990s but also more recent years saw successful
applications of this simple adversarial principle and its variants in
Reinforcement Learning (RL) settings, e.g.,
[SIN5]
[OUD13]
[PAT17]
[BUR18].
Q&As help to understand the world
which is necessary for planning
[PLAN] [PLAN2-6] [RES5-7]
and may boost external reward
[AC91] [AC97] [AC02] [PAT17]
[BUR18].
In the 2010s, the concepts of 1990
became popular as
compute became cheaper [DEC].
The term generative adversarial networks (GANs) is actually a
new name for a special case of the principle published in 1990
[AC90] [AC90b] [R2] [AC20]. GAN trials are
extremely short, consisting of a single action and a single environmental reaction, like in bandit problems.
In modern GAN terminology,
the controller C is called the generator, and the world model M the discriminator.
See also Sec. 5 of [MIR]
and
Sec. XVII of [T20],
and the closely related
Predictability Minimization
[PM0-2] [AC20] (applied to images in 1996 [PM2]).
2. 1991: Curiosity through maximizing learning progress
 The approach of 1990 [AC90] [AC90b] (Sec. 1) makes for a fine exploration strategy in many deterministic environments.
In stochastic environments, however, it might fail.
C might learn to focus on those
parts of the environment where M can always
get high prediction errors due to randomness,
or due to computational limitations of M.
For example, an agent controlled by C might get stuck in front of
a TV screen showing highly unpredictable white
noise [AC10].
The approach of 1990 [AC90] [AC90b] (Sec. 1) makes for a fine exploration strategy in many deterministic environments.
In stochastic environments, however, it might fail.
C might learn to focus on those
parts of the environment where M can always
get high prediction errors due to randomness,
or due to computational limitations of M.
For example, an agent controlled by C might get stuck in front of
a TV screen showing highly unpredictable white
noise [AC10].
Therefore, in stochastic environments,
C's reward should not be the errors of M,
but an approximation of the first derivative of M's errors across subsequent training iterations,
that is,
to prevent C from exploiting M too easily, C's reward should be
M's learning progress or improvements [AC91] [AC10] [PP2].
As a consequence, despite M's high errors in front of
the noisy TV above,
C won't get rewarded for getting stuck there,
simply because M's errors won't improve:
both the totally predictable and the fundamentally unpredictable will get boring.
3. 1995: RL for maximizing information gain or Bayesian surprise
The simple insight of 1991 (Sec. 2) led to lots of follow-up work [AC10].
One particular reinforcement learning (RL)
approach for artificial curiosity in stochastic environments was
published in 1995
with my former students Jan Storck and Sepp Hochreiter [AC95].
A simple world model M learned to predict or estimate the probabilities of the
environment's possible responses, given the actions of a controller C.
After each interaction with the environment,
C's intrinsic reward was the KL-Divergence [KUL]
between M's estimated probability distributions
before and after the resulting new experience, i.e.,
the information gain [AC95].
10 years later, this was dubbed Bayesian surprise [ITT5].
Compare earlier work on information gain [SHA]
and its maximization through active learning without RL & NNs [FED].
More formally, at a given time in a single lifelong trial,
M has seen the entire history H of C's sensory inputs and actions so far.
Now it is trying to predict the next sensory input Q, given H.
Suppose there are n possible values Q1, ..., Qn of Q.
For 0<i<n+1 (n and i are natural numbers),
M predicts the conditional probability pM(Qi|H) of Qi, given H.
Then Q is really observed.
Now M is trained
for some time on the observations so far to improve its predictions.
This yields an updated version of M called M*.
Q's contribution rint(Q) to C's intrinsic curiosity reward is
proportional to
∑i pM*(Qi|H) log (pM*(Qi|H) / pM(Qi|H)), the information gain about Q.
C's intrinsic joy is M's current learning progress.
Now the history H is prolonged by Q and we set M:=M* such that
M is ready to predict the next input observation.
Again, since the controller C is a reward maximizer, C is motivated to invent action sequences or experiments that yield data from which the world model M can still learn something.
C will get bored by well-known parts of the environment as well as by unpredictable noisy TVs [AC10].
2011: Bayes-optimal planning to be surprised.
My student Sun Yi et al.
showed that
C can optimally plan action sequences based on previous experiences
such that the cumulative expected information gain is maximized [AC11].
4. 1997: Adversarial agents design surprising computational experiments
 Before 1997, the questions asked by the controller C were restricted in the sense that they always referred to all the details of future inputs, e.g., pixels [AC90] [AC90b]. That's why in 1997, I built more general adversarial RL machines that could ignore many or all of these details and ask arbitrary abstract questions with computable answers [AC97] [AC99] [AC02]. For example, an agent may ask: if we run this policy (or program) for a while until it executes a special interrupt action, will the internal storage cell number 15 contain the value 5, or not? Again there are two learning, reward-maximizing adversaries playing a zero sum game, occasionally betting on different yes/no outcomes of such computational experiments. The winner of such a bet gets a reward of 1, the loser -1. So each adversary is motivated to come up with questions whose answers surprise the other. And both are motivated to avoid seemingly trivial questions where both already agree on the outcome, or seemingly hard questions that none of them can reliably answer for now.
Experiments showed that this type of curiosity may also accelerate the intake of external reward
[AC97] [AC02].
Before 1997, the questions asked by the controller C were restricted in the sense that they always referred to all the details of future inputs, e.g., pixels [AC90] [AC90b]. That's why in 1997, I built more general adversarial RL machines that could ignore many or all of these details and ask arbitrary abstract questions with computable answers [AC97] [AC99] [AC02]. For example, an agent may ask: if we run this policy (or program) for a while until it executes a special interrupt action, will the internal storage cell number 15 contain the value 5, or not? Again there are two learning, reward-maximizing adversaries playing a zero sum game, occasionally betting on different yes/no outcomes of such computational experiments. The winner of such a bet gets a reward of 1, the loser -1. So each adversary is motivated to come up with questions whose answers surprise the other. And both are motivated to avoid seemingly trivial questions where both already agree on the outcome, or seemingly hard questions that none of them can reliably answer for now.
Experiments showed that this type of curiosity may also accelerate the intake of external reward
[AC97] [AC02].
5. 2006: Maximizing compression progress like scientists and artists do
 I have frequently pointed out that
the history of science is a history of data compression progress through incremental discovery of simple laws that govern seemingly complex
observation sequences [AC06] [AC09] [AC10].
How to implement this principle in an artificial scientist based on a controller C and a predictive world model M?
Well, the better the predictions of M,
the fewer bits are required to encode the history H of sensory input observations,
because short codes
can be used for inputs that M considers highly probable [HUF].
That is, the learning progress of the M in the probabilistic inference machine of Sec. 3 above [AC95] has a lot to do with the concept of compression progress
[AC06] [AC09] [AC10].
However, it's not quite the same thing.
In particular, it does not take into account the bits of information needed to specify M and its re-trained version M*.
A more general approach is based on algorithmic information theory, e.g.,
[SOL] [KOL] [WA68]
[WA87] [LIV] [ALL2].
Here C's intrinsic reward is indeed based on algorithmic compression progress
[AC06] [AC09] [AC10].
Let us consider the history H up to the current input Q.
We introduce some coding scheme for the weights of the model network M, e.g., [FM]
[KO0-2] [CO1-4].
And also a coding scheme for the history of all observations so far, given M
[HUF] [WA68] [RIS]
[FM] [AC06].
(For example, already in 1991, my
first very deep learner based on unsupervised pre-training
used hierarchical predictive coding to find compact internal representations of sequential data to facilitate downstream learning [UN] [UN0-2].)
Now
I(M) bits are needed to describe H without ignoring the costs of the weights of M, and
I(M*) bits are necessary to describe H without ignoring the costs of the weights of M*.
Then C's total current curiosity reward or intrinsic joy or fun reflects M's depth of insight,
namely, the compression progress
I(M)-I(M*)
after having observed Q [AC06] [AC09] [AC10].
I have frequently pointed out that
the history of science is a history of data compression progress through incremental discovery of simple laws that govern seemingly complex
observation sequences [AC06] [AC09] [AC10].
How to implement this principle in an artificial scientist based on a controller C and a predictive world model M?
Well, the better the predictions of M,
the fewer bits are required to encode the history H of sensory input observations,
because short codes
can be used for inputs that M considers highly probable [HUF].
That is, the learning progress of the M in the probabilistic inference machine of Sec. 3 above [AC95] has a lot to do with the concept of compression progress
[AC06] [AC09] [AC10].
However, it's not quite the same thing.
In particular, it does not take into account the bits of information needed to specify M and its re-trained version M*.
A more general approach is based on algorithmic information theory, e.g.,
[SOL] [KOL] [WA68]
[WA87] [LIV] [ALL2].
Here C's intrinsic reward is indeed based on algorithmic compression progress
[AC06] [AC09] [AC10].
Let us consider the history H up to the current input Q.
We introduce some coding scheme for the weights of the model network M, e.g., [FM]
[KO0-2] [CO1-4].
And also a coding scheme for the history of all observations so far, given M
[HUF] [WA68] [RIS]
[FM] [AC06].
(For example, already in 1991, my
first very deep learner based on unsupervised pre-training
used hierarchical predictive coding to find compact internal representations of sequential data to facilitate downstream learning [UN] [UN0-2].)
Now
I(M) bits are needed to describe H without ignoring the costs of the weights of M, and
I(M*) bits are necessary to describe H without ignoring the costs of the weights of M*.
Then C's total current curiosity reward or intrinsic joy or fun reflects M's depth of insight,
namely, the compression progress
I(M)-I(M*)
after having observed Q [AC06] [AC09] [AC10].
How can we measure or at least
approximate the above-mentioned information-theoretic costs of M and M*?
Over the decades we have published several ways of learning to encode numerous weights of large NNs through very compact codes, e.g., [FM] [KO0-2] [CO1-4].
Here we exploited that the
Kolmogorov complexity or algorithmic information content of successful huge NNs may actually be rather small.
For example, in July 2013, the compact codes of
"Compressed Network Search" [CO2]
yielded the
first deep learning model to successfully learn control policies directly from high-dimensional
sensory input (video) using RL (in this case RL through neuroevolution),
without any
unsupervised pre-training.
 Read here how my Formal Theory of Fun
uses the concept of compression progress to explain not only science
but also art, music, and humor
[AC06] [AC09] [AC10].
Take humor for example.
Consider the following statement:
Biological organisms are driven by the "Four Big F's":
Feeding, Fighting, Fleeing, Mating.
Some subjective observers who read this for the first time think it is funny.
Why? As the eyes are sequentially
scanning the text the brain receives a complex visual input stream.
The latter is subjectively partially compressible as it relates to the
observer's previous knowledge about letters and words.
That is, given
the reader's current knowledge and current compressor, the raw data can be encoded
by fewer bits than required to store random data of the same size.
But the punch line after the last comma is unexpected for those who
expected another "F."
Initially this failed expectation results in sub-optimal
data compression—storage of expected events does not cost anything,
but deviations from predictions require extra bits to encode them.
The compressor, however, does not stay
the same forever: within a short time interval,
its learning algorithm kicks in and improves its performance on the data seen so far, by
discovering the non-random, non-arbitrary and therefore compressible pattern
relating the punch line to previous text and previous elaborate
predictive knowledge about the "Four Big F's."
This saves a few bits of storage. The number of saved bits
(or a similar measure of learning progress) becomes the observer's intrinsic
reward, possibly strong enough to
motivate her to read on in search for more
reward through additional yet unknown patterns.
While previous attempts at explaining humor also
focused on the element of surprise, e.g., [RAS85], they lacked the essential
concept of novel pattern detection measured by
compression progress due to learning [AC06] [AC09] [AC10].
This progress is zero whenever the
unexpected is just random white noise, and thus no fun at all.
Applications of my simple theory of humor can be found in
this old youtube video of a talk on
this subject which I gave at the Singularity Summit 2009 in NYC.
Read here how my Formal Theory of Fun
uses the concept of compression progress to explain not only science
but also art, music, and humor
[AC06] [AC09] [AC10].
Take humor for example.
Consider the following statement:
Biological organisms are driven by the "Four Big F's":
Feeding, Fighting, Fleeing, Mating.
Some subjective observers who read this for the first time think it is funny.
Why? As the eyes are sequentially
scanning the text the brain receives a complex visual input stream.
The latter is subjectively partially compressible as it relates to the
observer's previous knowledge about letters and words.
That is, given
the reader's current knowledge and current compressor, the raw data can be encoded
by fewer bits than required to store random data of the same size.
But the punch line after the last comma is unexpected for those who
expected another "F."
Initially this failed expectation results in sub-optimal
data compression—storage of expected events does not cost anything,
but deviations from predictions require extra bits to encode them.
The compressor, however, does not stay
the same forever: within a short time interval,
its learning algorithm kicks in and improves its performance on the data seen so far, by
discovering the non-random, non-arbitrary and therefore compressible pattern
relating the punch line to previous text and previous elaborate
predictive knowledge about the "Four Big F's."
This saves a few bits of storage. The number of saved bits
(or a similar measure of learning progress) becomes the observer's intrinsic
reward, possibly strong enough to
motivate her to read on in search for more
reward through additional yet unknown patterns.
While previous attempts at explaining humor also
focused on the element of surprise, e.g., [RAS85], they lacked the essential
concept of novel pattern detection measured by
compression progress due to learning [AC06] [AC09] [AC10].
This progress is zero whenever the
unexpected is just random white noise, and thus no fun at all.
Applications of my simple theory of humor can be found in
this old youtube video of a talk on
this subject which I gave at the Singularity Summit 2009 in NYC.
6. Does curiosity distort the basic RL problem?
The controller/model systems above (aka CM systems [PLAN4] [PLAN]) typically maximize the sum of
standard external rewards (for achieving user-given goals) and intrinsic curiosity rewards. Does this distort the basic RL problem? It turns out not so much.
Unlike the external reward for eating three times a day, the curiosity reward in the systems above is ephemeral, because once something is known, there is no additional intrinsic reward for discovering it again [AC10]. That is, the external reward tends to dominate the total reward. In totally learnable environments, in the long run, the intrinsic
reward even vanishes next to the external reward [AC10]. Which is nice, because in most RL applications we care only for the external reward.
7. Connections to metalearning since 1990
 The Section A Connection to Meta-Learning in [AC90] (1990) already pointed out:
"A model network can be used not only for predicting the controller's inputs but also for predicting its future outputs. A perfect model of this kind would model the internal changes of the control network. It would predict the evolution of the controller, and thereby the effects of the gradient descent procedure itself. In this case, the flow of activation in the model network would model the weight changes of the control network. This in turn comes close to the notion of learning how to learn."
The paper [AC90] also introduced
planning with recurrent NNs (RNNs) as world models [PLAN],
and high-dimensional reward signals.
Unlike in traditional RL,
those reward signals were also used as informative inputs to the controller NN
learning to execute actions that maximise cumulative reward
(see also Sec. 13 of [MIR]
and Sec. 5 of [DEC]).
This is important for metalearning: an NN that cannot see its own errors or rewards cannot learn
a better way of using such signals as inputs for self-invented learning algorithms.
The Section A Connection to Meta-Learning in [AC90] (1990) already pointed out:
"A model network can be used not only for predicting the controller's inputs but also for predicting its future outputs. A perfect model of this kind would model the internal changes of the control network. It would predict the evolution of the controller, and thereby the effects of the gradient descent procedure itself. In this case, the flow of activation in the model network would model the weight changes of the control network. This in turn comes close to the notion of learning how to learn."
The paper [AC90] also introduced
planning with recurrent NNs (RNNs) as world models [PLAN],
and high-dimensional reward signals.
Unlike in traditional RL,
those reward signals were also used as informative inputs to the controller NN
learning to execute actions that maximise cumulative reward
(see also Sec. 13 of [MIR]
and Sec. 5 of [DEC]).
This is important for metalearning: an NN that cannot see its own errors or rewards cannot learn
a better way of using such signals as inputs for self-invented learning algorithms.
A few years later, I combined Meta-RL and
Adversarial Artificial Curiosity in the system of Sec. 4 [AC97, AC99, AC02].
See also Sec. 6 of [META].
8. 2011: PowerPlay continually searches for novel formally well-defined computational problems whose solutions can easily be added to the skill repertoire, taking into account verification time
 My curious reinforcement learning Q&A systems of the 1990s
did not explicitly, formally enumerate their questions. But the more recent PowerPlay framework (2011)
[PP] [PPa] [PP1]
does. Let us step back for a moment. What is the set of all formalisable questions that any curious system could possibly ask? How to decide whether a given question has been answered by a learning machine? To define a question, we need a computational procedure that takes a solution candidate (possibly proposed by a policy) and decides whether it is an answer to the question or not. PowerPlay essentially enumerates the set of all such procedures (or some user-defined subset thereof), thus enumerating all possible questions or problems (including environments in which problems are to be solved).
It searches for the simplest question that the current policy cannot yet answer but can quickly learn to answer without forgetting the answers to previously answered questions. The computational costs of verifying that nothing has been forgotten are taken into account.
What is the simplest such Q&A to be added to the repertoire?
It is the cheapest one—the one that is found first.
Then the next trial starts, where new Q&As may build on previous Q&As.
Compare also the One Big Net For Everything [PLAN5] which offers a simplified, less strict NN
version of PowerPlay.
Also see the work from 2015 on RL robots learning to explore using high-dimensional video inputs and PowerPlay-like intrinsic motivation
[PP2].
My curious reinforcement learning Q&A systems of the 1990s
did not explicitly, formally enumerate their questions. But the more recent PowerPlay framework (2011)
[PP] [PPa] [PP1]
does. Let us step back for a moment. What is the set of all formalisable questions that any curious system could possibly ask? How to decide whether a given question has been answered by a learning machine? To define a question, we need a computational procedure that takes a solution candidate (possibly proposed by a policy) and decides whether it is an answer to the question or not. PowerPlay essentially enumerates the set of all such procedures (or some user-defined subset thereof), thus enumerating all possible questions or problems (including environments in which problems are to be solved).
It searches for the simplest question that the current policy cannot yet answer but can quickly learn to answer without forgetting the answers to previously answered questions. The computational costs of verifying that nothing has been forgotten are taken into account.
What is the simplest such Q&A to be added to the repertoire?
It is the cheapest one—the one that is found first.
Then the next trial starts, where new Q&As may build on previous Q&As.
Compare also the One Big Net For Everything [PLAN5] which offers a simplified, less strict NN
version of PowerPlay.
Also see the work from 2015 on RL robots learning to explore using high-dimensional video inputs and PowerPlay-like intrinsic motivation
[PP2].
The
PowerPlay paper (2011-13)
[PP] starts as follows:
"Most of computer science focuses on automatically solving given computational problems. I focus on automatically inventing or discovering problems in a way inspired by the playful behavior of animals and humans, to train a more and more general problem solver from scratch in an unsupervised fashion."
PowerPlay
can use the metalearning OOPS [OOPS1-3]
(Sec. 4 of [META])
to continually invent on its own new goals and tasks,
incrementally learning to become a more and more general problem solver in an active, partially unsupervised or self-supervised fashion.
9. 2015: Planning and curiosity with spatio-temporal abstractions in NNs
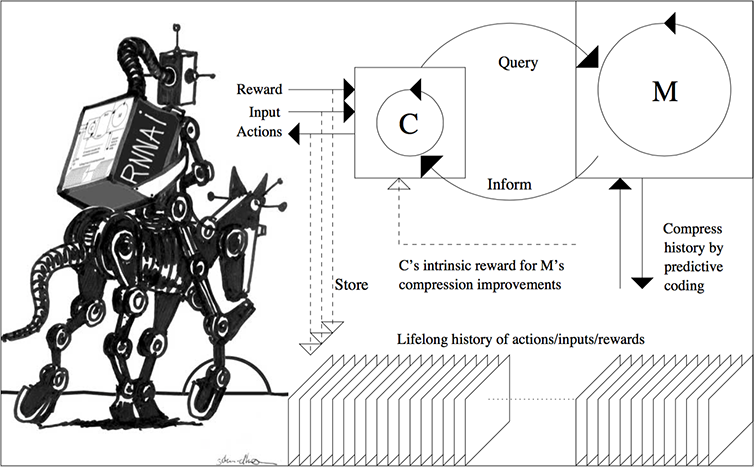
The recurrent controller/world model system of 1990 [AC90]
focused on naive "millisecond by millisecond planning,"
trying to predict and plan every little detail of its possible futures [PLAN].
Even today, this is
still a standard approach in many RL applications, e.g., RL for board games such as Chess and Go.
My more recent work of 2015, however, has
focused on abstract (e.g., hierarchical) planning and reasoning [PLAN4-5] [PLAN],
continuing the work of 1997 [AC97] [AC02] summarized in Sec. 4 above,
as well as early work on
hierarchical RL
since 1991 [HRL0-5]
(see also Sec. 10 of [MIR]).
Guided by
algorithmic information theory, I described recurrent NN-based AIs (RNNAIs) that can be trained on never-ending sequences of tasks, some of them provided by the user, others invented by the RNNAI itself in a curious, playful fashion, to improve its RNN-based world model. Unlike the system of 1990 [AC90], the RNNAI [PLAN4] learns to actively query its model for abstract reasoning and planning and decision making, essentially learning to think [PLAN4].
Compare also our recent related work on learning (hierarchically) structured
concept spaces based on abstract objects [OBJ2-5].
The ideas of [PLAN4-5] can be applied to many other cases where one RNN-like system exploits the algorithmic information content of another. They also explain concepts such as mirror neurons [PLAN4].
See also
recent work with David Ha
of Google (2018) [PLAN6]:
a world model that extracts compressed spatio-temporal representations which are fed into compact and simple policies trained by evolution, achieving state of the art results in various environments.
Agents with adaptive recurrent
world models even suggest
a simple explanation of consciousness and self-awareness
dating back three decades [PLAN] [UN] [CON16] [CATCH].
Acknowledgments
 Thanks to several expert reviewers for useful comments. Since science is about self-correction, let me know under juergen@idsia.ch if you can spot any remaining error. There is another version of this article with references in footnote style. The contents of this article may be used for educational and non-commercial purposes, including articles for Wikipedia and similar sites. This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Thanks to several expert reviewers for useful comments. Since science is about self-correction, let me know under juergen@idsia.ch if you can spot any remaining error. There is another version of this article with references in footnote style. The contents of this article may be used for educational and non-commercial purposes, including articles for Wikipedia and similar sites. This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
References
[ATT0] J. Schmidhuber and R. Huber.
Learning to generate focus trajectories for attentive vision.
Technical Report FKI-128-90, Institut für Informatik, Technische
Universität München, 1990.
PDF.
[ATT1] J. Schmidhuber and R. Huber. Learning to generate artificial fovea trajectories for target detection. International Journal of Neural Systems, 2(1 & 2):135-141, 1991. Based on TR FKI-128-90, TUM, 1990.
PDF.
More.
[ATT2]
J. Schmidhuber.
Learning algorithms for networks with internal and external feedback.
In D. S. Touretzky, J. L. Elman, T. J. Sejnowski, and G. E. Hinton,
editors, Proc. of the 1990 Connectionist Models Summer School, pages
52-61. San Mateo, CA: Morgan Kaufmann, 1990.
PS. (PDF.)
[HRL0]
J. Schmidhuber.
Towards compositional learning with dynamic neural networks.
Technical Report FKI-129-90, Institut für Informatik, Technische
Universität München, 1990.
PDF.
[HRL1]
J. Schmidhuber. Learning to generate sub-goals for action sequences. In T. Kohonen, K. Mäkisara, O. Simula, and J. Kangas, editors, Artificial Neural Networks, pages 967-972. Elsevier Science Publishers B.V., North-Holland, 1991. PDF. Extending TR FKI-129-90, TUM, 1990.
HTML & images in German.
[HRL2]
J. Schmidhuber and R. Wahnsiedler.
Planning simple trajectories using neural subgoal generators.
In J. A. Meyer, H. L. Roitblat, and S. W. Wilson, editors, Proc.
of the 2nd International Conference on Simulation of Adaptive Behavior,
pages 196-202. MIT Press, 1992.
PDF.
HTML & images in German.
[HRL4]
M. Wiering and J. Schmidhuber. HQ-Learning. Adaptive Behavior 6(2):219-246, 1997.
PDF.
[HRL5]
J. Schmidhuber.
Subgoal learning & hierarchical reinforcement learning since 1990.
(More.)
[PHD]
J. Schmidhuber.
Dynamische neuronale Netze und das fundamentale raumzeitliche
Lernproblem
(Dynamic neural nets and the fundamental spatio-temporal
credit assignment problem).
Dissertation,
Institut für Informatik, Technische
Universität München, 1990.
PDF.
HTML.
[PLAN2]
J. Schmidhuber.
An on-line algorithm for dynamic reinforcement learning and planning
in reactive environments.
In Proc. IEEE/INNS International Joint Conference on Neural
Networks, San Diego, volume 2, pages 253-258, June 17-21, 1990.
Based on [AC90].
[PLAN3]
J. Schmidhuber.
Reinforcement learning in Markovian and non-Markovian environments.
In D. S. Lippman, J. E. Moody, and D. S. Touretzky, editors,
Advances in Neural Information Processing Systems 3, NIPS'3, pages 500-506. San
Mateo, CA: Morgan Kaufmann, 1991.
PDF.
Partially based on [AC90].
[PLAN4]
J. Schmidhuber.
On Learning to Think: Algorithmic Information Theory for Novel Combinations of Reinforcement Learning Controllers and Recurrent Neural World Models.
Report arXiv:1210.0118 [cs.AI], 2015.
[PLAN5]
One Big Net For Everything. Preprint arXiv:1802.08864 [cs.AI], Feb 2018.
[PLAN6]
D. Ha, J. Schmidhuber. Recurrent World Models Facilitate Policy Evolution. Advances in Neural Information Processing Systems (NIPS), Montreal, 2018. (Talk.)
Preprint: arXiv:1809.01999.
Github: World Models.
[OBJ1] K. Greff, A. Rasmus, M. Berglund, T. Hao, H. Valpola, J. Schmidhuber (2016). Tagger: Deep unsupervised perceptual grouping. NIPS 2016, pp. 4484-4492.
[OBJ2] K. Greff, S. van Steenkiste, J. Schmidhuber (2017). Neural expectation maximization. NIPS 2017, pp. 6691-6701.
[OBJ3] S. van Steenkiste, M. Chang, K. Greff, J. Schmidhuber (2018). Relational neural expectation maximization: Unsupervised discovery of objects and their interactions. ICLR 2018.
[OBJ4]
A. Stanic, S. van Steenkiste, J. Schmidhuber (2021). Hierarchical Relational Inference. AAAI 2021.
[OBJ5]
A. Gopalakrishnan, S. van Steenkiste, J. Schmidhuber (2020). Unsupervised Object Keypoint Learning using Local Spatial Predictability.
In Proc. ICLR 2021.
Preprint arXiv/2011.12930.
[AC90]
J. Schmidhuber.
Making the world differentiable: On using fully recurrent
self-supervised neural networks for dynamic reinforcement learning and
planning in non-stationary environments.
Technical Report FKI-126-90, TUM, Feb 1990, revised Nov 1990.
PDF
[AC90b]
J. Schmidhuber.
A possibility for implementing curiosity and boredom in
model-building neural controllers.
In J. A. Meyer and S. W. Wilson, editors, Proc. of the
International Conference on Simulation
of Adaptive Behavior: From Animals to
Animats, pages 222-227. MIT Press/Bradford Books, 1991.
PDF.
HTML.
[AC91]
J. Schmidhuber. Adaptive confidence and adaptive curiosity. Technical Report FKI-149-91, Inst. f. Informatik, Tech. Univ. Munich, April 1991.
PDF.
[AC91b]
J. Schmidhuber.
Curious model-building control systems.
In Proc. International Joint Conference on Neural Networks,
Singapore, volume 2, pages 1458-1463. IEEE, 1991.
PDF.
[AC95]
J. Storck, S. Hochreiter, and J. Schmidhuber. Reinforcement-driven information acquisition in non-deterministic environments. In Proc. ICANN'95, vol. 2, pages 159-164. EC2 & CIE, Paris, 1995. PDF.
[AC97]
J. Schmidhuber.
What's interesting?
Technical Report IDSIA-35-97, IDSIA, July 1997.
[Focus
on automatic creation of predictable internal
abstractions of complex spatio-temporal events:
two competing, intrinsically motivated agents agree on essentially
arbitrary algorithmic experiments and bet
on their possibly surprising (not yet predictable)
outcomes in zero-sum games,
each agent potentially profiting from outwitting / surprising
the other by inventing experimental protocols where both
modules disagree on the predicted outcome. The focus is on exploring
the space of general algorithms (as opposed to
traditional simple mappings from inputs to
outputs); the
general system
focuses on the interesting
things by losing interest in both predictable and
unpredictable aspects of the world. Unlike our previous
systems with intrinsic motivation [AC90-AC95], the system also
takes into account
the computational cost of learning new skills, learning when to learn and what to learn.
Later publications on this: [AC99] [AC02].]
[AC98]
M. Wiering and J. Schmidhuber.
Efficient model-based exploration.
In R. Pfeiffer, B. Blumberg, J. Meyer, S. W. Wilson, eds.,
From Animals to Animats 5: Proceedings
of the Fifth International Conference on Simulation of Adaptive
Behavior, p. 223-228, MIT Press, 1998.
[AC98b]
M. Wiering and J. Schmidhuber.
Learning exploration policies with models.
In Proc. CONALD, 1998.
[AC99]
J. Schmidhuber.
Artificial Curiosity Based on Discovering Novel Algorithmic
Predictability Through Coevolution.
In P. Angeline, Z. Michalewicz, M. Schoenauer, X. Yao, Z.
Zalzala, eds., Congress on Evolutionary Computation, p. 1612-1618,
IEEE Press, Piscataway, NJ, 1999.
[AC02]
J. Schmidhuber.
Exploring the Predictable.
In Ghosh, S. Tsutsui, eds., Advances in Evolutionary Computing,
p. 579-612, Springer, 2002.
PDF.
[AC05]
J. Schmidhuber.
Self-Motivated Development Through
Rewards for Predictor Errors / Improvements.
Developmental Robotics 2005 AAAI Spring Symposium,
March 21-23, 2005, Stanford University, CA.
PDF.
[AC06]
J. Schmidhuber.
Developmental Robotics,
Optimal Artificial Curiosity, Creativity, Music, and the Fine Arts.
Connection Science, 18(2): 173-187, 2006.
PDF.
[AC07]
J. Schmidhuber.
Simple Algorithmic Principles of Discovery, Subjective Beauty,
Selective Attention, Curiosity & Creativity.
In V. Corruble, M. Takeda, E. Suzuki, eds.,
Proc. 10th Intl. Conf. on Discovery Science (DS 2007)
p. 26-38, LNAI 4755, Springer, 2007.
Also in M. Hutter, R. A. Servedio, E. Takimoto, eds.,
Proc. 18th Intl. Conf. on Algorithmic Learning Theory (ALT 2007)
p. 32, LNAI 4754, Springer, 2007.
(Joint invited lecture for DS 2007 and ALT 2007, Sendai, Japan, 2007.)
Preprint: arxiv:0709.0674.
PDF.
Curiosity as the drive to improve the compression
of the lifelong sensory input stream: interestingness as
the first derivative of subjective "beauty" or compressibility.
[AC08]
Driven by Compression Progress. In Proc.
Knowledge-Based Intelligent Information and
Engineering Systems KES-2008,
Lecture Notes in Computer Science LNCS 5177, p 11, Springer, 2008.
(Abstract of invited keynote talk.)
PDF.
[AC09]
J. Schmidhuber. Art & science as by-products of the search for novel patterns, or data compressible in unknown yet learnable ways. In M. Botta (ed.), Et al. Edizioni, 2009, pp. 98-112.
PDF. (More on
artificial scientists and artists.)
[AC09a]
J. Schmidhuber.
Driven by Compression Progress: A Simple Principle Explains Essential Aspects of Subjective Beauty, Novelty, Surprise, Interestingness, Attention, Curiosity, Creativity, Art, Science, Music, Jokes.
Based on keynote talk for KES 2008 (below) and joint invited
lecture for ALT 2007 / DS 2007 (below). Short version: ref 17 below. Long version in G. Pezzulo, M. V. Butz, O. Sigaud, G. Baldassarre, eds.: Anticipatory Behavior in Adaptive Learning Systems, from Sensorimotor to Higher-level Cognitive Capabilities, Springer, LNAI, 2009.
Preprint (2008, revised 2009): arXiv:0812.4360.
PDF (Dec 2008).
PDF (April 2009).
[AC09b]
J. Schmidhuber.
Simple Algorithmic Theory of Subjective Beauty, Novelty, Surprise,
Interestingness, Attention, Curiosity, Creativity, Art,
Science, Music, Jokes. Journal of SICE, 48(1):21-32, 2009.
PDF.
[AC10]
J. Schmidhuber. Formal Theory of Creativity, Fun, and Intrinsic Motivation (1990-2010). IEEE Transactions on Autonomous Mental Development, 2(3):230-247, 2010.
IEEE link.
PDF.
[AC10a]
J. Schmidhuber. Artificial Scientists & Artists Based on the Formal Theory of Creativity.
In
Proceedings of the Third Conference on Artificial General Intelligence (AGI-2010), Lugano, Switzerland.
PDF.
[AC11]
Sun Yi, F. Gomez, J. Schmidhuber.
Planning to Be Surprised: Optimal Bayesian Exploration in Dynamic Environments.
In Proc. Fourth Conference on Artificial General Intelligence (AGI-11),
Google, Mountain View, California, 2011.
PDF.
[AC11a]
V. Graziano, T. Glasmachers, T. Schaul, L. Pape, G. Cuccu, J. Leitner, J. Schmidhuber. Artificial Curiosity for Autonomous Space Exploration. Acta Futura 4:41-51, 2011 (DOI: 10.2420/AF04.2011.41). PDF.
[AC11b]
G. Cuccu, M. Luciw, J. Schmidhuber, F. Gomez.
Intrinsically Motivated Evolutionary Search for Vision-Based Reinforcement Learning.
In Proc. Joint IEEE International Conference on Development and Learning (ICDL) and on Epigenetic Robotics (ICDL-EpiRob 2011), Frankfurt, 2011.
PDF.
[AC11c]
M. Luciw, V. Graziano, M. Ring, J. Schmidhuber.
Artificial Curiosity with Planning for Autonomous Visual and Perceptual Development.
In Proc. Joint IEEE International Conference on Development and Learning (ICDL) and on Epigenetic Robotics (ICDL-EpiRob 2011), Frankfurt, 2011.
PDF.
[AC11d]
T. Schaul, L. Pape, T. Glasmachers, V. Graziano J. Schmidhuber.
Coherence Progress: A Measure of Interestingness Based on Fixed Compressors.
In Proc. Fourth Conference on Artificial General Intelligence (AGI-11),
Google, Mountain View, California, 2011.
PDF.
[AC11e]
T. Schaul, Yi Sun, D. Wierstra, F. Gomez, J. Schmidhuber. Curiosity-Driven Optimization. IEEE Congress on Evolutionary Computation (CEC-2011), 2011.
PDF.
[AC11f]
H. Ngo, M. Ring, J. Schmidhuber.
Curiosity Drive based on Compression Progress for Learning Environment Regularities.
In Proc. Joint IEEE International Conference on Development and Learning (ICDL) and on Epigenetic Robotics (ICDL-EpiRob 2011), Frankfurt, 2011.
[AC12]
L. Pape, C. M. Oddo, M. Controzzi, C. Cipriani, A. Foerster, M. C. Carrozza, J. Schmidhuber.
Learning tactile skills through curious exploration.
Frontiers in Neurorobotics 6:6, 2012, doi: 10.3389/fnbot.2012.00006
[AC12a]
H. Ngo, M. Luciw, A. Foerster, J. Schmidhuber.
Learning Skills from Play: Artificial Curiosity on a Katana Robot Arm.
Proc. IJCNN 2012.
PDF.
Video.
[AC12b]
V. R. Kompella, M. Luciw, M. Stollenga, L. Pape, J. Schmidhuber.
Autonomous Learning of Abstractions using Curiosity-Driven Modular Incremental Slow Feature Analysis.
Proc. IEEE Conference on Development and Learning / EpiRob 2012
(ICDL-EpiRob'12), San Diego, 2012.
[AC12c]
J. Schmidhuber. Maximizing Fun By Creating Data With Easily Reducible Subjective Complexity.
In G. Baldassarre and M. Mirolli (eds.), Roadmap for Intrinsically Motivated Learning.
Springer, 2012.
[AC20]
J. Schmidhuber. Generative Adversarial Networks are Special Cases of Artificial Curiosity (1990) and also Closely Related to Predictability Minimization (1991).
Neural Networks, Volume 127, p 58-66, 2020.
Preprint arXiv/1906.04493.
[R2] Reddit/ML, 2019. J. Schmidhuber really had GANs in 1990.
[PP] J. Schmidhuber.
POWERPLAY: Training an Increasingly General Problem Solver by Continually Searching for the Simplest Still Unsolvable Problem.
Frontiers in Cognitive Science, 2013.
ArXiv preprint (2011):
arXiv:1112.5309 [cs.AI]
[PPa]
R. K. Srivastava, B. R. Steunebrink, M. Stollenga, J. Schmidhuber.
Continually Adding Self-Invented
Problems to the Repertoire: First
Experiments with POWERPLAY.
Proc. IEEE Conference on Development and Learning / EpiRob 2012
(ICDL-EpiRob'12), San Diego, 2012.
PDF.
[PP1] R. K. Srivastava, B. Steunebrink, J. Schmidhuber.
First Experiments with PowerPlay.
Neural Networks, 2013.
ArXiv preprint (2012):
arXiv:1210.8385 [cs.AI].
[PP2] V. Kompella, M. Stollenga, M. Luciw, J. Schmidhuber. Continual curiosity-driven skill acquisition from high-dimensional video inputs for humanoid robots. Artificial Intelligence, 2015.
[OOPS1]
J. Schmidhuber. Bias-Optimal Incremental Problem Solving.
In S. Becker, S. Thrun, K. Obermayer, eds.,
Advances in Neural Information Processing Systems 15, N(eur)IPS'15, MIT Press, Cambridge MA, p. 1571-1578, 2003.
PDF
[OOPS2]
J. Schmidhuber.
Optimal Ordered Problem Solver.
Machine Learning, 54, 211-254, 2004.
PDF.
HTML.
HTML overview.
Download
OOPS source code in crystalline format.
[OOPS3]
Schmidhuber, J., Zhumatiy, V. and Gagliolo, M. Bias-Optimal
Incremental Learning of Control Sequences for Virtual Robots. In Groen,
F., Amato, N., Bonarini, A., Yoshida, E., and Kroese, B., editors:
Proceedings of the 8-th conference
on Intelligent Autonomous Systems, IAS-8, Amsterdam,
The Netherlands, pp. 658-665, 2004.
PDF.
[RES5]
Gloye, A., Wiesel, F., Tenchio, O., Simon, M. Reinforcing the Driving
Quality of Soccer Playing Robots by Anticipation, IT - Information
Technology, vol. 47, nr. 5, Oldenbourg Wissenschaftsverlag, 2005.
PDF.
[RES7]
J. Schmidhuber: Prototype resilient, self-modeling robots. Correspondence, Science, 316, no. 5825 p 688, May 2007.
[PM0] J. Schmidhuber. Learning factorial codes by predictability minimization. TR CU-CS-565-91, Univ. Colorado at Boulder, 1991. PDF.
More.
[PM1] J. Schmidhuber. Learning factorial codes by predictability minimization. Neural Computation, 4(6):863-879, 1992. PDF.
More.
[PM2] J. Schmidhuber, M. Eldracher, B. Foltin. Semilinear predictability minimzation produces well-known feature detectors. Neural Computation, 8(4):773-786, 1996.
PDF. More.
[KO0]
J. Schmidhuber.
Discovering problem solutions with low Kolmogorov complexity and
high generalization capability.
Technical Report FKI-194-94, Fakultät für Informatik,
Technische Universität München, 1994.
PDF.
[KO1] J. Schmidhuber.
Discovering solutions with low Kolmogorov complexity
and high generalization capability.
In A. Prieditis and S. Russell, editors, Machine Learning:
Proceedings of the Twelfth International Conference (ICML 1995),
pages 488-496. Morgan
Kaufmann Publishers, San Francisco, CA, 1995.
PDF.
[KO2]
J. Schmidhuber.
Discovering neural nets with low Kolmogorov complexity
and high generalization capability.
Neural Networks, 10(5):857-873, 1997.
PDF.
[CO1]
J. Koutnik, F. Gomez, J. Schmidhuber (2010). Evolving Neural Networks in Compressed Weight Space. Proceedings of the Genetic and Evolutionary Computation Conference
(GECCO-2010), Portland, 2010.
PDF.
[CO2]
J. Koutnik, G. Cuccu, J. Schmidhuber, F. Gomez.
Evolving Large-Scale Neural Networks for Vision-Based Reinforcement Learning.
In Proceedings of the Genetic and Evolutionary
Computation Conference (GECCO), Amsterdam, July 2013.
PDF.
[CO3]
R. K. Srivastava, J. Schmidhuber, F. Gomez.
Generalized Compressed Network Search.
Proc. GECCO 2012.
PDF.
[CO4]
S. van Steenkiste, J. Koutnik, K. Driessens, J. Schmidhuber.
A wavelet-based encoding for neuroevolution.
Proceedings of the Genetic and Evolutionary Computation
Conference 2016, GECCO'16, pages 517-524, New York, NY, USA, 2016. ACM.
[SHA]
C. E. Shannon.
A mathematical theory of communication (parts I and II).
Bell System Technical Journal, XXVII:379-423, 1948.
[KUL]
S. Kullback and R. A. Leibler.
On information and sufficiency.
The Annals of Mathematical Statistics, pages 79-86, 1951.
[HUF]
D. A. Huffman.
A method for construction of minimum-redundancy codes.
Proceedings IRE, 40:1098-1101, 1952.
[SOL]
R. J. Solomonoff.
A formal theory of inductive inference. Part I.
Information and Control, 7:1-22, 1964.
[KOL]
A. N. Kolmogorov.
Three approaches to the quantitative definition of information.
Problems of Information Transmission, 1:1-11, 1965.
[FED]
V. V. Fedorov.
Theory of optimal experiments.
Academic Press, 1972.
[WA68]
C. S. Wallace and D. M. Boulton.
An information theoretic measure for classification.
Computer Journal, 11(2):185-194, 1968.
[WA87]
C. S. Wallace and P. R. Freeman.
Estimation and inference by compact coding.
Journal of the Royal Statistical Society, Series "B",
49(3):240-265, 1987.
[RIS]
J. Rissanen.
Modeling by shortest data description.
Automatica, 14:465-471, 1978.
[LIV]
M. Li and P. M. B. Vitanyi.
An Introduction to Kolmogorov Complexity and its Applications
(2nd edition).
Springer, 1997.
[ALL2]
J. Schmidhuber (2000).
Algorithmic theories of everything.
ArXiv:
quant-ph/ 0011122.
See also:
International Journal of Foundations of Computer Science 13(4):587-612, 2002:
PDF.
See also: Proc. COLT 2002:
PDF.
More.
[FM]
S. Hochreiter and J. Schmidhuber.
Flat minimum search finds simple nets.
Technical Report FKI-200-94, Fakultät für Informatik,
Technische Universität München, December 1994.
PDF.
[RAS85]
V. Raskin (1985).
Semantic Mechanisms of Humor. Dordrecht & Boston & Lancaster, 1985.
[SIN5]
S. Singh, A. G. Barto, N. Chentanez.
Intrinsically motivated reinforcement learning.
In Advances in Neural Information Processing Systems 17
(NIPS). MIT Press, Cambridge, MA, 2005.
[ITT5]
L. Itti, P. F. Baldi.
Bayesian surprise attracts human attention.
In Advances in Neural Information Processing Systems (NIPS) 19,
pages 547-554. MIT Press, Cambridge, MA, 2005.
[OUD13]
P.-Y. Oudeyer, A. Baranes, F. Kaplan.
Intrinsically motivated learning of real world sensorimotor skills
with developmental constraints.
In G. Baldassarre and M. Mirolli, editors, Intrinsically
Motivated Learning in Natural and Artificial Systems. Springer, 2013.
[PAT17]
D. Pathak, P. Agrawal, A. A. Efros, T. Darrell.
Curiosity-driven exploration by self-supervised prediction.
In Proceedings of the IEEE Conference on Computer Vision and
Pattern Recognition Workshops, pages 16-17, 2017.
[BUR18]
Y. Burda, H. Edwards, D. Pathak, A. Storkey, T. Darrell, A. A. Efros.
Large-scale study of curiosity-driven learning.
Preprint arXiv:1808.04355, 2018.
[UN0]
J. Schmidhuber.
Neural sequence chunkers.
Technical Report FKI-148-91, Institut für Informatik, Technische
Universität München, April 1991.
PDF.
[UN1]
J. Schmidhuber. Learning complex, extended sequences using the principle of history compression. Neural Computation, 4(2):234-242, 1992. Based on TR FKI-148-91, TUM, 1991 [UN0]. PDF.
[First working Deep Learner based on a deep RNN hierarchy (with different self-organizing time scales), overcoming the vanishing gradient problem through unsupervised pre-training and predictive coding. Also: compressing or distilling a teacher net (the chunker) into a student net (the automatizer) that does not forget its old skills—such approaches are now widely used. More.]
[UN2] J. Schmidhuber. Habilitation thesis, TUM, 1993. PDF.
[An ancient experiment on "Very Deep Learning" with credit assignment across 1200 time steps or virtual layers and unsupervised pre-training for a stack of recurrent NN
can be found here (depth > 1000).]
[UN3]
J. Schmidhuber, M. C. Mozer, and D. Prelinger.
Continuous history compression.
In H. Hüning, S. Neuhauser, M. Raus, and W. Ritschel, editors,
Proc. of Intl. Workshop on Neural Networks, RWTH Aachen, pages 87-95.
Augustinus, 1993.
[SNT]
J. Schmidhuber, S. Heil (1996).
Sequential neural text compression.
IEEE Trans. Neural Networks, 1996.
PDF.
(An earlier version appeared at NIPS 1995.)
[CATCH]
J. Schmidhuber. Philosophers & Futurists, Catch Up! Response to The Singularity.
Journal of Consciousness Studies, Volume 19, Numbers 1-2, pp. 173-182(10), 2012.
PDF.
[CON16]
J. Carmichael (2016).
Artificial Intelligence Gained Consciousness in 1991.
Why A.I. pioneer Jürgen Schmidhuber is convinced the ultimate breakthrough already happened.
Inverse, 2016. Link.
[DL1] J. Schmidhuber, 2015.
Deep Learning in neural networks: An overview. Neural Networks, 61, 85-117.
More.
[DL2] J. Schmidhuber, 2015.
Deep Learning.
Scholarpedia, 10(11):32832.
[DL4] J. Schmidhuber, 2017. Our impact on the world's most valuable public companies: 1. Apple, 2. Alphabet (Google), 3. Microsoft, 4. Facebook, 5. Amazon ...
HTML.
[T20] J. Schmidhuber (June 2020). Critique of 2018 Turing Award.
[MIR] J. Schmidhuber (10/4/2019). Deep Learning: Our Miraculous Year 1990-1991. See also arxiv:2005.05744 (May 2020).
[DEC] J. Schmidhuber (02/20/2020). The 2010s: Our Decade of Deep Learning / Outlook on the 2020s.
[ATT] J. Schmidhuber (2020). 30-year anniversary of end-to-end differentiable sequential neural attention. Plus goal-conditional reinforcement learning. We had both hard attention (1990) and soft attention (1993). Today, both types are very popular.
[META]
J. Schmidhuber (2020). 1/3 century anniversary of
first publication on metalearning machines that learn to learn (1987).
For its cover I drew a robot that bootstraps itself.
1992-: gradient descent-based neural metalearning. 1994-: Meta-Reinforcement Learning with self-modifying policies. 1997: Meta-RL plus artificial curiosity and intrinsic motivation.
2002-: asymptotically optimal metalearning for curriculum learning. 2003-: mathematically optimal Gödel Machine. 2020: new stuff!
[UN]
J. Schmidhuber (2021). 30-year anniversary. 1991: First very deep learning with unsupervised pre-training. Unsupervised hierarchical predictive coding finds compact internal representations of sequential data to facilitate downstream learning. The hierarchy can be distilled into a single deep neural network (suggesting a simple model of conscious and subconscious information processing). 1993: solving problems of depth >1000.
[PLAN]
J. Schmidhuber (2020). 30-year anniversary of planning & reinforcement learning with recurrent world models and artificial curiosity (1990). This work also introduced high-dimensional reward signals, deterministic policy gradients for RNNs,
the GAN principle (widely used today). Agents with adaptive recurrent world models even suggest a simple explanation of consciousness & self-awareness.
.


