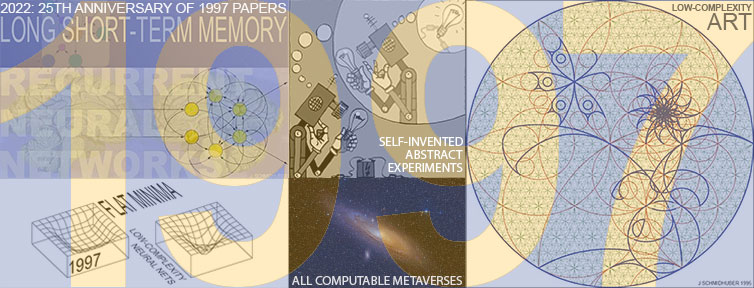
Abstract.
1997 was a great year for me. I married my wonderful wife, became a father, and—for the first time—bought a car more expensive than my bike. In what follows, however, I'll focus on the 25-year anniversaries of our 1997 publications on Artificial Intelligence (AI), physics, and the fine arts. Many of them are relevant now as modern AI
is dominated by artificial neural networks (NNs),[DL1-4] and foundations of the most popular NNs originated in my labs at TU Munich and IDSIA.[MOST] In 2022, we are celebrating the following works from a quarter-century ago:
Sec. 1: Journal paper on Long Short-Term Memory,[LSTM1] the
most cited NN of the 20th century
(and basis[HW1,3] of the most cited NN of the 21st[HW2]).
Sec. 2: First paper[ALL1] on physical, philosophical and theological consequences of the simplest and fastest way of computing
all possible metaverses
(= computable universes).[ALL1-3]
Sec. 3:
Implementing artificial curiosity and creativity[AC90-20] through generative adversarial agents that learn to design abstract, interesting computational experiments.[AC97][AC02]
Sec. 4: Journal paper on
meta-reinforcement learning.[METARL7]
Sec. 5: Journal paper[HRL4] on hierarchical Q-learning.
Sec. 6: First paper on reinforcement learning to play soccer:[SOC1] start of a series.[SOC1-5]
Sec. 7:
Journal papers on flat minima & low-complexity NNs that generalize well.[KO2][FM2]
Sec. 8:
Journal paper on Low-Complexity Art.[ART2]
Sec. 9:
Journal paper on probabilistic incremental program evolution.[PIPE]

According to Google Scholar, no other computer science paper of the 20th century is receiving as many citations per year as our 1997 journal publication on Long Short-Term Memory (LSTM) artificial neural networks (NNs).[LSTM1] LSTMs are now permeating the modern world, with innumerable applications
including in healthcare,[DEC] learning robots,[LSTM-RL][LSTMPG][OAI1,1a]
game playing,[LSTMPG][OAI2,2a][DM3]
speech processing,[AM16][GSR][GSR15-19]
and machine translation.[GT16][WU][FB17][DEC] They are used billions of times a day by countless people.[DL4] This led Bloomberg to say LSTM is "arguably the most commercial AI achievement."[AV1][DL4][MIR](Sec. 4) LSTMs as we know them today go beyond earlier work[MOZ] and were
made possible through my students
Sepp Hochreiter (first author of the famous paper),
Felix Gers, Alex Graves,
Daan Wierstra, and others.[VAN1][LSTM0-17,PG]
The LSTM principle is also the foundation of our Highway Net made possible through my PhD students Rupesh Kumar Srivastava and Klaus Greff (May 2015, patented by NNAISENSE in 2021),[HW1-3] the first working very deep feedforward NN with over 100 layers (previous NNs had at most a few tens of layers). Half a year later, an NN equivalent to a Highway Net whose gates are initialized such that they remain always open was republished under the name "ResNet" (Dec 2015) in what's now
the most cited NN paper of the 21st century.[HW2]
That is, the most popular NNs of both centuries are based on the LSTM principle.

In the 1940s,
Konrad Zuse, the man who built the world's first working general-purpose computer (1935-1941),[ZUS21,a,b]
speculated that our universe might be computable by a deterministic computer program,
like the virtual worlds of today's video games.[ALL3] He published scientific works on this in the 1960s.[ZU67][ZU69]
Morton Heilig patented a virtual reality machine called Sensorama in 1957.[HEIL57] SF author Daniel F. Galouye described adventures in virtual universes in 1964.[GAL64] The term "metaverse" was coined in 1992 by SF author Neil Stephenson.[STE92]
In 1997, I published my first paper (submitted in 1996) on an Algorithmic Theory of Everything: the simplest and fastest way of computing
all logically possible, computable universes
(or metaverses). Ours may be one of them. The paper was called
A Computer Scientist's View of Life, the Universe, and Everything.[ALL1] It was inspired by my brother Christof (the physicist) who—since we were boys in the 1970s—kept telling me that the universe is essentially the sum of all mathematics. It took me a while to figure out what that means from a computational perspective, and the philosophical and theological consequences thereof. The 1997 abstract goes like this:[ALL1]
Is the universe computable? If so, it may be much cheaper in terms of information requirements to compute all computable universes instead of just ours. I apply basic concepts of
Kolmogorov complexity theory to the set of possible universes, and chat about perceived and true randomness, life, generalization, and learning in a given universe.
In follow-up work of 2000, I published additional technical breakthroughs regarding the set of all formally describable things, in particular, all the metaverses computable by non-halting programs.[ALL2] 20 years ago, this was also published at COLT 2002[ALL2a] and in IJFCS (2002).[ALL2b] See the 2012 summary[ALL3] and the overview page on the optimally efficient computation of all logically possible metaverses. Assuming our universe is computed by this optimal method,
we can predict that it is among the fastest compatible with our existence.
This yields non-trivial testable predictions.[ALL1-ALL3] For example, unfortunately, the most desirable form of quantum computation will never work.[ALL2]
The fact that there are mathematically optimal ways of creating and computing all the logically possible worlds also opens a new and exciting approach to fundamental questions of philosophy and theology.[ALL1-ALL3]
In 2012, the famous blockbuster actor Morgan Freeman featured my work on
all computable metaverses
in the US TV Premiere of Through the Wormhole on the Science Channel.

Since 1990, I have published work about artificial scientists equipped with artificial curiosity and creativity,[AC,AC90-AC20][PP-PP2] pointing out that there are two important things in science:
(A) Finding answers to given questions, and (B) Coming up with good questions.
(A) is arguably just the standard problem of computer science. But
how to implement the creative part (B) in artificial systems through
reinforcement learning (RL),
gradient-based artificial neural networks (NNs),
and other machine learning methods?
My first artificial Q&A system designed to invent and answer questions
was the intrinsic motivation-based adversarial system from 1990.[AC90][AC90b] It employs two artificial neural networks (NNs) that duel each other.
One NN—the controller—probabilistically generates outputs.
Another NN—the world model—sees the outputs of the controller and predicts environmental reactions to them. Using gradient descent, the predictor NN minimizes its error, while the generator NN tries to make outputs that maximize this error: one net's loss is the other net's gain. A well-known 2010 survey[AC10] summarised the generative adversarial NNs of 1990 as follows: a
"neural network as a predictive world model is used to maximize the controller's intrinsic reward, which is proportional to the model's prediction errors" (which are minimized). The so-called
GANs[GAN1][R2][MOST] are a version of this where the trials are very short (like in bandit problems) and the environment simply returns 1 or 0 depending on whether the controller's (or generator's) output is in a given set.[AC20][AC] Compare Sec. XVII of Technical Report IDSIA-77-21.[T21]
Before 1997, however, the questions asked by the controller were restricted in the sense that they included all the details of environmental reactions, e.g., pixels.[AC90][AC90b] That's why in 1997, I published more general adversarial RL machines that could ignore many or all of these details and ask arbitrary abstract questions with computable answers[AC97][AC99] (this was republished in 2002[AC02]). For example, an agent may ask: if we run this policy (or program) for a while until it executes a special interrupt action, will the internal storage cell number 15 contain the value 5, or not? Again there are two learning, reward-maximizing adversaries playing a zero sum game, occasionally betting on different yes/no outcomes of such computational experiments. The winner of such a bet gets a reward of 1, the loser -1. So each adversary is motivated to come up with questions whose answers surprise the other. And both are motivated to avoid seemingly trivial questions where both already agree on the outcome, or seemingly hard questions that none of them can reliably answer for now.
Experiments have shown that this type of curiosity may also accelerate the intake of external reward.[AC97][AC02]

1987 saw my first publication on
metalearning or learning to learn the learning algorithm itself:
my
diploma thesis of 1987.[META1][R3][META]
In 1994, I published
meta-reinforcement learning with
self-modifying policies.[METARL2-9]
In 1997, this finally led to the first journal publication on this topic, with my PhD student Marco Wiering and my PostDoc Jieyu Zhao.[METARL7] Here is the abstract:
We study task sequences that allow for speeding up the learner's average reward intake through appropriate shifts of inductive bias (changes of the learner's policy). To evaluate long-term effects of bias shifts setting the stage for later bias shifts we use the ``success-story algorithm'' (SSA). SSA is occasionally called at times that may depend on the policy itself. It uses backtracking to undo those bias shifts that have not been empirically observed to trigger long-term reward accelerations (measured up until the current SSA call). Bias shifts that survive SSA represent a lifelong success history. Until the next SSA call, they are considered useful and build the basis for additional bias shifts. SSA allows for plugging in a wide variety of learning algorithms. We plug in (1) a novel, adaptive extension of Levin search and (2) a method for embedding the learner's policy modification strategy within the policy itself (incremental self-improvement). Our inductive transfer case studies involve complex, partially observable environments where traditional reinforcement learning fails.
Check out the overview in this 2022 YouTube video on metalearning in a single lifelong trial as well as our most recent papers (2020-2022) on meta-RL[METARL10]
and metalearning, self-modifying, self-referential weight matrices[FWPMETA8-9] (extending previous work[FWP0-5][FWPMETA1-7]).
Traditional Reinforcement Learning (RL) without a teacher does not hierarchically decompose problems into
easier subproblems.[HRLW] That's why in 1990 I introduced Hierarchical RL (HRL) with
end-to-end differentiable NN-based subgoal generators,[HRL0] also with
recurrent NNs that learn to generate sequences of subgoals.[HRL1-2]
Our 1990-91 papers[HRL0-1] started a long series of papers on HRL.
Our journal paper on Hierarchical Q-Learning was accepted 25 years ago, in 1997.[HRL4] It was made possible through my PhD student Marco Wiering. Here is the abstract:
HQ-learning is a hierarchical extension of Q(lambda)-learning designed to solve certain types of partially observable Markov decision problems (POMDPs). HQ automatically decomposes POMDPs into sequences of simpler subtasks that can be solved by memoryless policies learnable by reactive subagents. HQ can solve partially observable mazes with more states than those used in most previous POMDP work.
 In 1997, we also published the first paper on reinforcement learning to play soccer.[SOC1] This was made possible through my PhD students Rafal Salustowicz and Marco Wiering.
It started a long series of papers on this topic.[SOC1-5] Here is the abstract:
In 1997, we also published the first paper on reinforcement learning to play soccer.[SOC1] This was made possible through my PhD students Rafal Salustowicz and Marco Wiering.
It started a long series of papers on this topic.[SOC1-5] Here is the abstract:
We study multiagent learning in a simulated soccer scenario. Players from the same team share a common policy for mapping inputs to actions. They get rewarded or punished collectively in case of goals. For varying team sizes we compare the following learning algorithms: TD-Q learning with linear neural networks (TD-Q-LIN), with a neural gas network (TD-Q-NG), Probabilistic Incremental Program Evolution (PIPE), and a PIPE variant based on coevolution (CO-PIPE). TD-Q-LIN and TD-Q-NG try to learn evaluation functions (EFs) mapping input-action pairs to expected reward. PIPE and CO-PIPE search policy space directly. They use adaptive probability distributions to synthesize programs that calculate action probabilities from current inputs. We find that learning appropriate EFs is hard for both EF-based approaches. Direct search in policy space discovers more reliable policies and is faster.
 This work was part of a long chain of works on evolution and neuroevolution for reinforcement learning, including
Genetic Programming for code of unlimited size (1987),
co-evolving recurrent neurons (2005-), Evolino (2005-2008), Natural Evolution Strategies (2009-), Compressed Network Search (e.g., 1995, 2013), and many other works.
This work was part of a long chain of works on evolution and neuroevolution for reinforcement learning, including
Genetic Programming for code of unlimited size (1987),
co-evolving recurrent neurons (2005-), Evolino (2005-2008), Natural Evolution Strategies (2009-), Compressed Network Search (e.g., 1995, 2013), and many other works.
My former postdoc Alexander Gloye-Foerster led the FU-Fighters team that became
robocup world champion 2004
in the fastest league (robot speed up to 5m/s)—see my overview page on learning robots.

Many NNs can learn their training data. But they often fail to generalize on unseen test data.
In 1997, we published two journal papers on discovering low-complexity NNs with high generalization power.[KO2][FM2]
In line with Occam's Razor, we exploited that the
Kolmogorov complexity or algorithmic information content of successful huge NNs may actually be rather small[KO0-1][FM,FM1] (compare later work on Compressed Network Search[CO2]). Here is the abstract of the paper on Flat Minimum Search, made possible through my PhD student Sepp Hochreiter:[FM2]
We present a new algorithm for finding low complexity neural networks with high generalization capability. The algorithm searches for a "flat" minimum of the error function. A flat minimum is a large connected region in weight space where the error remains approximately constant. An MDL-based, Bayesian argument suggests that flat minima correspond to "simple" networks and low expected overfitting. The argument is based on a Gibbs algorithm variant and a novel way of splitting generalization error into underfitting and overfitting error. Unlike many previous approaches, ours does not require Gaussian assumptions and does not depend on a ``good'' weight prior—instead we have a prior over input/output functions, thus taking into account net architecture and training set. Although our algorithm requires the computation of second order derivatives, it has backprop's order of complexity. Automatically, it effectively prunes units, weights, and input lines. Various experiments with feedforward and recurrent nets are described. In an application to stock market prediction, flat minimum search outperforms (1) conventional backprop, (2) weight decay, (3) "optimal brain surgeon" / "optimal brain damage."
And here is the abstract of the paper on finding simple NNs with low algorithmic information that can be computed by short computer programs:[KO2]
Many neural net learning algorithms aim at finding "simple" nets to explain training data. The expectation is: the "simpler" the networks, the better the generalization on test data (Occam's razor). Previous implementations, however, use measures for "simplicity" that lack the power, universality and elegance of those based on Kolmogorov complexity and Solomonoff's algorithmic probability. Likewise, most previous approaches (especially those of the "Bayesian" kind) suffer from the problem of choosing appropriate priors. This paper addresses both issues. It first reviews some basic concepts of algorithmic complexity theory relevant to machine learning, and how the Solomonoff-Levin distribution (or universal prior) deals with the prior problem. The universal prior leads to a probabilistic method for finding "algorithmically simple" problem solutions with high generalization capability. The method is based on Levin complexity (a time-bounded generalization of Kolmogorov complexity) and inspired by Levin's optimal universal search algorithm. For a given problem, solution candidates are computed by efficient "self-sizing" programs that influence their own runtime and storage size. The probabilistic search algorithm finds the "good" programs (the ones quickly computing algorithmically probable solutions fitting the training data). Simulations focus on the task of discovering "algorithmically simple" neural networks with low Kolmogorov complexity and high generalization capability. It is demonstrated that the method, at least with certain toy problems where it is computationally feasible, can lead to generalization results unmatchable by previous neural net algorithms. Much remains do be done, however, to make large scale applications and "incremental learning" feasible.

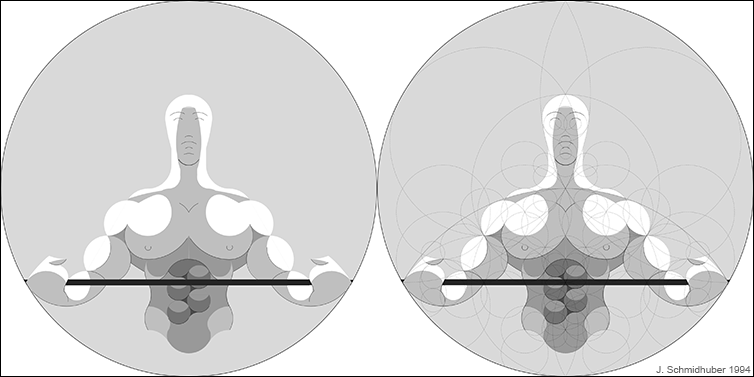
In 1997, I also published the first journal paper[ART2] on Low-Complexity Art[ART1] in Leonardo, the leading journal on science and the fine arts. Here the abstract:
Many artists when representing an object try to convey its "essence." In an attempt to formalize certain aspects of depicting the essence of objects, the author proposes an art form called low-complexity art. It may be viewed as the computer-age equivalent of minimal art. Its goals are based on concepts from algorithmic information theory. A low-complexity artwork can be specified by a computer algorithm and should comply with two properties: (1) the drawing should "look right," and (2) the Kolmogorov complexity of the drawing should be small (the algorithm should be short) and a typical observer should be able to see this. Examples of low-complexity art are given in the form of algorithmically simple cartoons of various objects. Attempts are made to relate the formalism of the theory of minimum description length to informal notions such as "good artistic style" and "beauty."
See my overview page with numerous links to papers on
artificial scientists and artists, the formal theory of beauty, interestingness, and fun.[AC06-AC10c]

Here is the abstract of the 1997 journal paper on PIPE, made possible through my PhD student Rafal Salustowicz:[PIPE]
Probabilistic incremental program evolution (PIPE) is a novel technique for automatic program synthesis. We combine probability vector coding of program instructions, population-based incremental learning, and tree-coded programs like those used in some variants of genetic programming (GP). PIPE iteratively generates successive populations of functional programs according to an adaptive probability distribution over all possible programs. Each iteration, it uses the best program to refine the distribution. Thus, it stochastically generates better and better programs. Since distribution refinements depend only on the best program of the current population, PIPE can evaluate program populations efficiently when the goal is to discover a program with minimal runtime. We compare PIPE to GP on a function regression problem and the 6-bit parity problem. We also use PIPE to solve tasks in partially observable mazes, where the best programs have minimal runtime.
1997 was also the year when our Swiss AI Lab IDSIA was ranked for the first time among the world's top ten AI labs (in the "X-Lab Survey" by Business Week Magazine—the other members of the top 10 club were much larger than IDSIA). IDSIA also was ranked 4th in the category "biologically inspired." It should be mentioned though that quite a few of the 1997 journal papers actually were based on our previous work since the early 1990s.
Click here for more groundbreaking 1997 publications of our team!
Acknowledgments
Thanks to Dylan Ashley, David Ha, and Sepp Hochreiter, for useful comments.
 The contents of this article may be used for educational and non-commercial purposes, including articles for Wikipedia and similar sites. This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
The contents of this article may be used for educational and non-commercial purposes, including articles for Wikipedia and similar sites. This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
References
[AC]
J. Schmidhuber (AI Blog, 2021). 3 decades of artificial curiosity & creativity. Our artificial scientists not only answer given questions but also invent new questions. They achieve curiosity through: (1990) the principle of generative adversarial networks, (1991) neural nets that maximise learning progress, (1995) neural nets that maximise information gain (optimally since 2011), (1997) adversarial design of surprising computational experiments, (2006) maximizing compression progress like scientists/artists/comedians do, (2011) PowerPlay... Since 2012: applications to real robots.
[AC90]
J. Schmidhuber.
Making the world differentiable: On using fully recurrent
self-supervised neural networks for dynamic reinforcement learning and
planning in non-stationary environments.
Technical Report FKI-126-90, TUM, Feb 1990, revised Nov 1990.
PDF.
The first paper on planning with reinforcement learning recurrent neural networks (NNs) (more) and on generative adversarial networks
where a generator NN is fighting a predictor NN in a minimax game
(more).
[AC90b]
J. Schmidhuber.
A possibility for implementing curiosity and boredom in
model-building neural controllers.
In J. A. Meyer and S. W. Wilson, editors, Proc. of the
International Conference on Simulation
of Adaptive Behavior: From Animals to
Animats, pages 222-227. MIT Press/Bradford Books, 1991.
PDF.
More.
[AC91]
J. Schmidhuber. Adaptive confidence and adaptive curiosity. Technical Report FKI-149-91, Inst. f. Informatik, Tech. Univ. Munich, April 1991.
PDF.
[AC91b]
J. Schmidhuber.
Curious model-building control systems.
Proc. International Joint Conference on Neural Networks,
Singapore, volume 2, pages 1458-1463. IEEE, 1991.
PDF.
[AC95]
J. Storck, S. Hochreiter, and J. Schmidhuber. Reinforcement-driven information acquisition in non-deterministic environments. In Proc. ICANN'95, vol. 2, pages 159-164. EC2 & CIE, Paris, 1995. PDF.
[AC97]
J. Schmidhuber.
What's interesting?
Technical Report IDSIA-35-97, IDSIA, July 1997.
[Focus
on automatic creation of predictable internal
abstractions of complex spatio-temporal events:
two competing, intrinsically motivated agents agree on essentially
arbitrary algorithmic experiments and bet
on their possibly surprising (not yet predictable)
outcomes in zero-sum games,
each agent potentially profiting from outwitting / surprising
the other by inventing experimental protocols where both
modules disagree on the predicted outcome. The focus is on exploring
the space of general algorithms (as opposed to
traditional simple mappings from inputs to
outputs); the
general system
focuses on the interesting
things by losing interest in both predictable and
unpredictable aspects of the world. Unlike our previous
systems with intrinsic motivation,[AC90-AC95] the system also
takes into account
the computational cost of learning new skills, learning when to learn and what to learn.
See later publications.[AC99][AC02]]
[AC98]
M. Wiering and J. Schmidhuber.
Efficient model-based exploration.
In R. Pfeiffer, B. Blumberg, J. Meyer, S. W. Wilson, eds.,
From Animals to Animats 5: Proceedings
of the Fifth International Conference on Simulation of Adaptive
Behavior, p. 223-228, MIT Press, 1998.
[AC98b]
M. Wiering and J. Schmidhuber.
Learning exploration policies with models.
In Proc. CONALD, 1998.
[AC99]
J. Schmidhuber.
Artificial Curiosity Based on Discovering Novel Algorithmic
Predictability Through Coevolution.
In P. Angeline, Z. Michalewicz, M. Schoenauer, X. Yao, Z.
Zalzala, eds., Congress on Evolutionary Computation, p. 1612-1618,
IEEE Press, Piscataway, NJ, 1999.
[AC02]
J. Schmidhuber.
Exploring the Predictable.
In Ghosh, S. Tsutsui, eds., Advances in Evolutionary Computing,
p. 579-612, Springer, 2002.
PDF.
[AC05]
J. Schmidhuber.
Self-Motivated Development Through
Rewards for Predictor Errors / Improvements.
Developmental Robotics 2005 AAAI Spring Symposium,
March 21-23, 2005, Stanford University, CA.
PDF.
[AC06]
J. Schmidhuber.
Developmental Robotics,
Optimal Artificial Curiosity, Creativity, Music, and the Fine Arts.
Connection Science, 18(2): 173-187, 2006.
PDF.
[AC07]
J. Schmidhuber.
Simple Algorithmic Principles of Discovery, Subjective Beauty,
Selective Attention, Curiosity & Creativity.
In V. Corruble, M. Takeda, E. Suzuki, eds.,
Proc. 10th Intl. Conf. on Discovery Science (DS 2007)
p. 26-38, LNAI 4755, Springer, 2007.
Also in M. Hutter, R. A. Servedio, E. Takimoto, eds.,
Proc. 18th Intl. Conf. on Algorithmic Learning Theory (ALT 2007)
p. 32, LNAI 4754, Springer, 2007.
(Joint invited lecture for DS 2007 and ALT 2007, Sendai, Japan, 2007.)
Preprint: arxiv:0709.0674.
PDF.
Curiosity as the drive to improve the compression
of the lifelong sensory input stream: interestingness as
the first derivative of subjective "beauty" or compressibility.
[AC08]
Driven by Compression Progress. In Proc.
Knowledge-Based Intelligent Information and
Engineering Systems KES-2008,
Lecture Notes in Computer Science LNCS 5177, p 11, Springer, 2008.
(Abstract of invited keynote talk.)
PDF.
[AC09]
J. Schmidhuber. Art & science as by-products of the search for novel patterns, or data compressible in unknown yet learnable ways. In M. Botta (ed.), Et al. Edizioni, 2009, pp. 98-112.
PDF. (More on
artificial scientists and artists.)
[AC09a]
J. Schmidhuber.
Driven by Compression Progress: A Simple Principle Explains Essential Aspects of Subjective Beauty, Novelty, Surprise, Interestingness, Attention, Curiosity, Creativity, Art, Science, Music, Jokes.
Based on keynote talk for KES 2008 (below) and joint invited
lecture for ALT 2007 / DS 2007 (below). Short version: ref 17 below. Long version in G. Pezzulo, M. V. Butz, O. Sigaud, G. Baldassarre, eds.: Anticipatory Behavior in Adaptive Learning Systems, from Sensorimotor to Higher-level Cognitive Capabilities, Springer, LNAI, 2009.
Preprint (2008, revised 2009): arXiv:0812.4360.
PDF (Dec 2008).
PDF (April 2009).
[AC09b]
J. Schmidhuber.
Simple Algorithmic Theory of Subjective Beauty, Novelty, Surprise,
Interestingness, Attention, Curiosity, Creativity, Art,
Science, Music, Jokes. Journal of SICE, 48(1):21-32, 2009.
PDF.
[AC10]
J. Schmidhuber. Formal Theory of Creativity, Fun, and Intrinsic Motivation (1990-2010). IEEE Transactions on Autonomous Mental Development, 2(3):230-247, 2010.
IEEE link.
PDF.
[AC10a]
J. Schmidhuber. Artificial Scientists & Artists Based on the Formal Theory of Creativity.
In
Proceedings of the Third Conference on Artificial General Intelligence (AGI-2010), Lugano, Switzerland.
PDF.
[AC11]
Sun Yi, F. Gomez, J. Schmidhuber.
Planning to Be Surprised: Optimal Bayesian Exploration in Dynamic Environments.
In Proc. Fourth Conference on Artificial General Intelligence (AGI-11),
Google, Mountain View, California, 2011.
PDF.
[AC11a]
V. Graziano, T. Glasmachers, T. Schaul, L. Pape, G. Cuccu, J. Leitner, J. Schmidhuber. Artificial Curiosity for Autonomous Space Exploration. Acta Futura 4:41-51, 2011 (DOI: 10.2420/AF04.2011.41). PDF.
[AC11b]
G. Cuccu, M. Luciw, J. Schmidhuber, F. Gomez.
Intrinsically Motivated Evolutionary Search for Vision-Based Reinforcement Learning.
In Proc. Joint IEEE International Conference on Development and Learning (ICDL) and on Epigenetic Robotics (ICDL-EpiRob 2011), Frankfurt, 2011.
PDF.
[AC11c]
M. Luciw, V. Graziano, M. Ring, J. Schmidhuber.
Artificial Curiosity with Planning for Autonomous Visual and Perceptual Development.
In Proc. Joint IEEE International Conference on Development and Learning (ICDL) and on Epigenetic Robotics (ICDL-EpiRob 2011), Frankfurt, 2011.
PDF.
[AC11d]
T. Schaul, L. Pape, T. Glasmachers, V. Graziano J. Schmidhuber.
Coherence Progress: A Measure of Interestingness Based on Fixed Compressors.
In Proc. Fourth Conference on Artificial General Intelligence (AGI-11),
Google, Mountain View, California, 2011.
PDF.
[AC11e]
T. Schaul, Yi Sun, D. Wierstra, F. Gomez, J. Schmidhuber. Curiosity-Driven Optimization. IEEE Congress on Evolutionary Computation (CEC-2011), 2011.
PDF.
[AC11f]
H. Ngo, M. Ring, J. Schmidhuber.
Curiosity Drive based on Compression Progress for Learning Environment Regularities.
In Proc. Joint IEEE International Conference on Development and Learning (ICDL) and on Epigenetic Robotics (ICDL-EpiRob 2011), Frankfurt, 2011.
[AC12]
L. Pape, C. M. Oddo, M. Controzzi, C. Cipriani, A. Foerster, M. C. Carrozza, J. Schmidhuber.
Learning tactile skills through curious exploration.
Frontiers in Neurorobotics 6:6, 2012, doi: 10.3389/fnbot.2012.00006
[AC12a]
H. Ngo, M. Luciw, A. Foerster, J. Schmidhuber.
Learning Skills from Play: Artificial Curiosity on a Katana Robot Arm.
Proc. IJCNN 2012.
PDF.
Video.
[AC12b]
V. R. Kompella, M. Luciw, M. Stollenga, L. Pape, J. Schmidhuber.
Autonomous Learning of Abstractions using Curiosity-Driven Modular Incremental Slow Feature Analysis.
Proc. IEEE Conference on Development and Learning / EpiRob 2012
(ICDL-EpiRob'12), San Diego, 2012.
[AC12c]
J. Schmidhuber. Maximizing Fun By Creating Data With Easily Reducible Subjective Complexity.
In G. Baldassarre and M. Mirolli (eds.), Roadmap for Intrinsically Motivated Learning.
Springer, 2012.
[AC20]
J. Schmidhuber. Generative Adversarial Networks are Special Cases of Artificial Curiosity (1990) and also Closely Related to Predictability Minimization (1991).
Neural Networks, Volume 127, p 58-66, 2020.
Preprint arXiv/1906.04493.
[ALL1]
A Computer Scientist's View of Life, the Universe, and Everything.
LNCS 201-288, Springer, 1997 (submitted 1996).
PDF.
More.
[ALL2]
Algorithmic theories of everything
(2000).
ArXiv:
quant-ph/ 0011122.
See also:
International Journal of Foundations of Computer Science 13(4):587-612, 2002:
PDF.
See also: Proc. COLT 2002:
PDF.
More.
[ALL2a]
The Speed Prior: A New Simplicity Measure
Yielding Near-Optimal Computable Predictions.
In J. Kivinen and R. H. Sloan, editors, Proceedings of the 15th
Annual Conference on Computational Learning Theory (COLT 2002), Sydney, Australia,
Lecture Notes in Artificial Intelligence, pages 216--228. Springer, 2002.
PDF.
HTML.
Based on section 6 of [ALL2].
[ALL2b]
Hierarchies of generalized Kolmogorov complexities and
nonenumerable universal measures computable in the limit.
International Journal of Foundations of Computer Science 13(4):587-612, 2002.
PDF.
PS.
Based on sections 2-5 of of [ALL2].
[ALL2c]
J. Schmidhuber:
Randomness in physics (Correspondence, Nature 439 p 392, Jan 2006)
[ALL2d]
J. Schmidhuber. Alle berechenbaren Universen. (All computable universes.)
Spektrum der Wissenschaft (German edition of Scientific American),
2007, Spezial 3/07, p. 75-79, 2007.
PDF.
[ALL3]
J. Schmidhuber. The Fastest Way of Computing All Universes. In H. Zenil, ed.,
A Computable Universe.
World Scientific, 2012. PDF of preprint.
More.
[ART1]
J. Schmidhuber.
Low-Complexity Art.
Report FKI-197-94, Fakultät für Informatik, Technische
Universität München, 1994.
PDF.
[ART2]
J. Schmidhuber.
Low-Complexity Art.
Leonardo, Journal of the
International Society for the Arts, Sciences, and
Technology, 30(2):97-103, MIT Press, 1997.
PDF.
HTML.
Based on [ART1].
[AV1] A. Vance. Google Amazon and Facebook Owe Jürgen Schmidhuber a Fortune—This Man Is the Godfather the AI Community Wants to Forget. Business Week,
Bloomberg, May 15, 2018.
[CO1]
J. Koutnik, F. Gomez, J. Schmidhuber (2010). Evolving Neural Networks in Compressed Weight Space. Proceedings of the Genetic and Evolutionary Computation Conference
(GECCO-2010), Portland, 2010.
PDF.
[CO2]
J. Koutnik, G. Cuccu, J. Schmidhuber, F. Gomez.
Evolving Large-Scale Neural Networks for Vision-Based Reinforcement Learning.
In Proceedings of the Genetic and Evolutionary
Computation Conference (GECCO), Amsterdam, July 2013.
PDF.
[CO3]
R. K. Srivastava, J. Schmidhuber, F. Gomez.
Generalized Compressed Network Search.
Proc. GECCO 2012.
PDF.
[DEC] J. Schmidhuber (AI Blog, 02/20/2020; revised 2021). The 2010s: Our Decade of Deep Learning / Outlook on the 2020s. The recent decade's most important developments and industrial applications based on our AI, with an outlook on the 2020s, also addressing privacy and data markets.
[DEEP1]
Ivakhnenko, A. G. and Lapa, V. G. (1965). Cybernetic Predicting Devices. CCM Information Corporation. First working Deep Learners with many layers, learning internal representations.
[DEEP1a]
Ivakhnenko, Alexey Grigorevich. The group method of data of handling; a rival of the method of stochastic approximation. Soviet Automatic Control 13 (1968): 43-55.
[DEEP2]
Ivakhnenko, A. G. (1971). Polynomial theory of complex systems. IEEE Transactions on Systems, Man and Cybernetics, (4):364-378.
[DL1] J. Schmidhuber, 2015.
Deep learning in neural networks: An overview. Neural Networks, 61, 85-117.
More.
Got the first Best Paper Award ever issued by the journal Neural Networks, founded in 1988.
[DL2] J. Schmidhuber, 2015.
Deep Learning.
Scholarpedia, 10(11):32832.
[DL4] J. Schmidhuber (AI Blog, 2017).
Our impact on the world's most valuable public companies: Apple, Google, Microsoft, Facebook, Amazon... By 2015-17, neural nets developed in my labs were on over 3 billion devices such as smartphones, and used many billions of times per day, consuming a significant fraction of the world's compute. Examples: greatly improved (CTC-based) speech recognition on all Android phones, greatly improved machine translation through Google Translate and Facebook (over 4 billion LSTM-based translations per day), Apple's Siri and Quicktype on all iPhones, the answers of Amazon's Alexa, etc. Google's 2019
on-device speech recognition
(on the phone, not the server)
is still based on
LSTM.
[DM3]
S. Stanford. DeepMind's AI, AlphaStar Showcases Significant Progress Towards AGI. Medium ML Memoirs, 2019.
Alphastar has a "deep LSTM core."
[DNC] Hybrid computing using a neural network with dynamic external memory.
A. Graves, G. Wayne, M. Reynolds, T. Harley, I. Danihelka, A. Grabska-Barwinska, S. G. Colmenarejo, E. Grefenstette, T. Ramalho, J. Agapiou, A. P. Badia, K. M. Hermann, Y. Zwols, G. Ostrovski, A. Cain, H. King, C. Summerfield, P. Blunsom, K. Kavukcuoglu, D. Hassabis.
Nature, 538:7626, p 471, 2016.
[FWP]
J. Schmidhuber (AI Blog, 26 March 2021).
26 March 1991: Neural nets learn to program neural nets with fast weights—like Transformer variants. 2021: New stuff!
30-year anniversary of a now popular
alternative[FWP0-1] to recurrent NNs.
A slow feedforward NN learns by gradient descent to program the changes of
the fast weights[FAST,FASTa] of
another NN.
Such Fast Weight Programmers[FWP0-6,FWPMETA1-7] can learn to memorize past data, e.g.,
by computing fast weight changes through additive outer products of self-invented activation patterns[FWP0-1]
(now often called keys and values for self-attention[TR1-6]).
The similar Transformers[TR1-2] combine this with projections
and softmax and
are now widely used in natural language processing.
For long input sequences, their efficiency was improved through
linear Transformers or Performers[TR5-6]
which are formally equivalent to the 1991 Fast Weight Programmers (apart from normalization).
In 1993, I introduced
the attention terminology[FWP2] now used
in this context,[ATT] and
extended the approach to
RNNs that program themselves.
[FWP0]
J. Schmidhuber.
Learning to control fast-weight memories: An alternative to recurrent nets.
Technical Report FKI-147-91, Institut für Informatik, Technische
Universität München, 26 March 1991.
PDF.
First paper on fast weight programmers: a slow net learns by gradient descent to compute weight changes of a fast net.
[FWP1] J. Schmidhuber. Learning to control fast-weight memories: An alternative to recurrent nets. Neural Computation, 4(1):131-139, 1992.
PDF.
HTML.
Pictures (German).
[FWP2] J. Schmidhuber. Reducing the ratio between learning complexity and number of time-varying variables in fully recurrent nets. In Proceedings of the International Conference on Artificial Neural Networks, Amsterdam, pages 460-463. Springer, 1993.
PDF.
First recurrent fast weight programmer based on outer products. Introduced the terminology of learning "internal spotlights of attention."
[FWP3] I. Schlag, J. Schmidhuber. Gated Fast Weights for On-The-Fly Neural Program Generation. Workshop on Meta-Learning, @N(eur)IPS 2017, Long Beach, CA, USA.
[FWP3a] I. Schlag, J. Schmidhuber. Learning to Reason with Third Order Tensor Products. Advances in Neural Information Processing Systems (N(eur)IPS), Montreal, 2018.
Preprint: arXiv:1811.12143. PDF.
[FWP5]
F. J. Gomez and J. Schmidhuber.
Evolving modular fast-weight networks for control.
In W. Duch et al. (Eds.):
Proc. ICANN'05,
LNCS 3697, pp. 383-389, Springer-Verlag Berlin Heidelberg, 2005.
PDF.
HTML overview.
Reinforcement-learning fast weight programmer.
[FWP6]
I. Schlag, K. Irie, J. Schmidhuber. Linear Transformers Are Secretly Fast Weight Programmers. ICML 2021.
Preprint: arXiv:2102.11174. See also the
Blog Post.
[FWP7] K. Irie, I. Schlag, R. Csordas, J. Schmidhuber. Going Beyond Linear Transformers with Recurrent Fast Weight Programmers.
Advances in Neural Information Processing Systems (NeurIPS), 2021.
Preprint: arXiv:2106.06295. See also the
Blog Post.
[FWPMETA1] J. Schmidhuber. Steps towards `self-referential' learning. Technical Report CU-CS-627-92, Dept. of Comp. Sci., University of Colorado at Boulder, November 1992.
First recurrent fast weight programmer that can learn
to run a learning algorithm or weight change algorithm on itself.
[FWPMETA2] J. Schmidhuber. A self-referential weight matrix.
In Proceedings of the International Conference on Artificial
Neural Networks, Amsterdam, pages 446-451. Springer, 1993.
PDF.
[FWPMETA3] J. Schmidhuber.
An introspective network that can learn to run its own weight change algorithm. In Proc. of the Intl. Conf. on Artificial Neural Networks,
Brighton, pages 191-195. IEE, 1993.
[FWPMETA4]
J. Schmidhuber.
A neural network that embeds its own meta-levels.
In Proc. of the International Conference on Neural Networks '93,
San Francisco. IEEE, 1993.
[FWPMETA5]
J. Schmidhuber. Habilitation thesis, TUM, 1993. PDF.
A recurrent neural net with a self-referential, self-reading, self-modifying weight matrix
can be found here.
[FWPMETA7]
I. Schlag, T. Munkhdalai, J. Schmidhuber.
Learning Associative Inference Using Fast Weight Memory.
International Conference on Learning Representations (ICLR 2021).
Preprint: arXiv:2011.07831 [cs.AI], 2020.
[FWPMETA8]
L. Kirsch, J. Schmidhuber. Meta Learning Backpropagation And Improving It.
Advances in Neural Information Processing Systems (NeurIPS), 2021.
Preprint: arXiv:2012.14905.
[FWPMETA9]
K. Irie, I. Schlag, R. Csordas, J. Schmidhuber.
A Modern Self-Referential Weight Matrix That Learns to Modify Itself.
International Conference on Machine Learning (ICML), 2022.
Preprint: arXiv:2202.05780.
[FB17]
By 2017, Facebook
used LSTM
to handle
over 4 billion automatic translations per day (The Verge, August 4, 2017);
see also
Facebook blog by J.M. Pino, A. Sidorov, N.F. Ayan (August 3, 2017)
[FM]
S. Hochreiter and J. Schmidhuber.
Flat minimum search finds simple nets.
Technical Report FKI-200-94, Fakultät für Informatik,
Technische Universität München, December 1994.
PDF.
[FM1]
S. Hochreiter and J. Schmidhuber.
Simplifying neural nets by discovering flat minima.
In G. Tesauro, D. S. Touretzky and T. K. Leen, eds.,
Advances in Neural Information Processing Systems 7, NIPS'7,
pages 529-536.
MIT Press, Cambridge MA, 1995.
PDF.
HTML.
[FM2]
S. Hochreiter and J. Schmidhuber.
Flat Minima.
Neural Computation, 9(1):1-42, 1997.
PDF.
HTML.
[GAL64]
D. F. Galouye (1964). Simulacron-3. UK title: Counterfeit World.
[GAN0]
O. Niemitalo. A method for training artificial neural networks to generate missing data within a variable context.
Blog post, Internet Archive, 2010.
A blog post describing the basic ideas[AC][AC90, AC90b][AC20] of GANs.
[GAN1]
I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair,
A. Courville, Y. Bengio.
Generative adversarial nets. NIPS 2014, 2672-2680, Dec 2014.
Description of GANs that does not cite the original work of 1990[AC][AC90, AC90b][AC20][R2] (also containing wrong claims about
Predictability Minimization[PM0-2][AC20]).
[GSR]
H. Sak, A. Senior, K. Rao, F. Beaufays, J. Schalkwyk—Google Speech Team.
Google voice search: faster and more accurate.
Google Research Blog, Sep 2015, see also
Aug 2015 Google's speech recognition based on CTC and LSTM.
[GSR15] Dramatic
improvement of Google's speech recognition through LSTM:
Alphr Technology, Jul 2015, or 9to5google, Jul 2015
[GSR19]
Y. He, T. N. Sainath, R. Prabhavalkar, I. McGraw, R. Alvarez, D. Zhao, D. Rybach, A. Kannan, Y. Wu, R. Pang, Q. Liang, D. Bhatia, Y. Shangguan, B. Li, G. Pundak, K. Chai Sim, T. Bagby, S. Chang, K. Rao, A. Gruenstein.
Streaming end-to-end speech recognition for mobile devices. ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2019.
[GT16] Google's
dramatically improved Google Translate of 2016 is based on LSTM, e.g.,
WIRED, Sep 2016,
or
siliconANGLE, Sep 2016
[HEIL57]
H. Brockwell. Forgotten genius: the man who made a working VR machine in 1957. Tech Radar, 2016.
[HRLW]
C. Watkins (1989). Learning from delayed rewards.
[HRL0]
J. Schmidhuber.
Towards compositional learning with dynamic neural networks.
Technical Report FKI-129-90, Institut für Informatik, Technische
Universität München, 1990.
PDF.
[HRL1]
J. Schmidhuber. Learning to generate sub-goals for action sequences. In T. Kohonen, K. Mäkisara, O. Simula, and J. Kangas, editors, Artificial Neural Networks, pages 967-972. Elsevier Science Publishers B.V., North-Holland, 1991. PDF. Extending TR FKI-129-90, TUM, 1990.
HTML & images in German.
[HRL2]
J. Schmidhuber and R. Wahnsiedler.
Planning simple trajectories using neural subgoal generators.
In J. A. Meyer, H. L. Roitblat, and S. W. Wilson, editors, Proc.
of the 2nd International Conference on Simulation of Adaptive Behavior,
pages 196-202. MIT Press, 1992.
PDF.
HTML & images in German.
[HRL4]
M. Wiering and J. Schmidhuber. HQ-Learning. Adaptive Behavior 6(2):219-246, 1997.
PDF.
[HW1] R. K. Srivastava, K. Greff, J. Schmidhuber. Highway networks.
Preprints arXiv:1505.00387 (May 2015) and arXiv:1507.06228 (July 2015). Also at NIPS 2015. The first working very deep feedforward nets with over 100 layers (previous NNs had at most a few tens of layers). Let g, t, h, denote non-linear differentiable functions. Each non-input layer of a highway net computes g(x)x + t(x)h(x), where x is the data from the previous layer. (Like LSTM with forget gates[LSTM2] for RNNs.) Resnets[HW2] are a version of this where the gates are always open: g(x)=t(x)=const=1.
Highway Nets perform roughly as well as ResNets[HW2] on ImageNet.[HW3] Highway layers are also often used for natural language processing, where the simpler residual layers do not work as well.[HW3]
More.
[HW1a]
R. K. Srivastava, K. Greff, J. Schmidhuber. Highway networks. Presentation at the Deep Learning Workshop, ICML'15, July 10-11, 2015.
Link.
[HW2] He, K., Zhang,
X., Ren, S., Sun, J. Deep residual learning for image recognition. Preprint
arXiv:1512.03385
(Dec 2015). Residual nets are a version of Highway Nets[HW1]
where the gates are always open:
g(x)=1 (a typical highway net initialization) and t(x)=1.
More.
[HW3]
K. Greff, R. K. Srivastava, J. Schmidhuber. Highway and Residual Networks learn Unrolled Iterative Estimation. Preprint
arxiv:1612.07771 (2016). Also at ICLR 2017.
[KO0]
J. Schmidhuber.
Discovering problem solutions with low Kolmogorov complexity and
high generalization capability.
Technical Report FKI-194-94, Fakultät für Informatik,
Technische Universität München, 1994.
PDF.
[KO1]
J. Schmidhuber.
Discovering solutions with low Kolmogorov complexity
and high generalization capability.
In A. Prieditis and S. Russell, editors, Machine Learning:
Proceedings of the Twelfth International Conference (ICML 1995),
pages 488-496. Morgan
Kaufmann Publishers, San Francisco, CA, 1995.
PDF.
HTML.
[KO2]
J. Schmidhuber.
Discovering neural nets with low Kolmogorov complexity
and high generalization capability.
Neural Networks, 10(5):857-873, 1997.
PDF.
[LSTM0]
S. Hochreiter and J. Schmidhuber.
Long Short-Term Memory.
TR FKI-207-95, TUM, August 1995.
PDF.
[LSTM1] S. Hochreiter, J. Schmidhuber. Long Short-Term Memory. Neural Computation, 9(8):1735-1780, 1997. PDF.
Based on [LSTM0]. More.
[LSTM2] F. A. Gers, J. Schmidhuber, F. Cummins. Learning to Forget: Continual Prediction with LSTM. Neural Computation, 12(10):2451-2471, 2000.
PDF.
The "vanilla LSTM architecture" with forget gates
that everybody is using today, e.g., in Google's Tensorflow.
[LSTM3] A. Graves, J. Schmidhuber. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Networks, 18:5-6, pp. 602-610, 2005.
PDF.
[LSTM4]
S. Fernandez, A. Graves, J. Schmidhuber. An application of
recurrent neural networks to discriminative keyword
spotting.
Intl. Conf. on Artificial Neural Networks ICANN'07,
2007.
PDF.
[LSTM5] A. Graves, M. Liwicki, S. Fernandez, R. Bertolami, H. Bunke, J. Schmidhuber. A Novel Connectionist System for Improved Unconstrained Handwriting Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 5, 2009.
PDF.
[LSTM6] A. Graves, J. Schmidhuber. Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks. NIPS'22, p 545-552, Vancouver, MIT Press, 2009.
PDF.
[LSTM7] J. Bayer, D. Wierstra, J. Togelius, J. Schmidhuber.
Evolving memory cell structures for sequence learning.
Proc. ICANN-09, Cyprus, 2009.
PDF.
[LSTM8] A. Graves, A. Mohamed, G. E. Hinton. Speech Recognition with Deep Recurrent Neural Networks. ICASSP 2013, Vancouver, 2013.
PDF.
[LSTM9]
O. Vinyals, L. Kaiser, T. Koo, S. Petrov, I. Sutskever, G. Hinton.
Grammar as a Foreign Language. Preprint arXiv:1412.7449 [cs.CL].
[LSTM10]
A. Graves, D. Eck and N. Beringer, J. Schmidhuber. Biologically Plausible Speech Recognition with LSTM Neural Nets. In J. Ijspeert (Ed.), First Intl. Workshop on Biologically Inspired Approaches to Advanced Information Technology, Bio-ADIT 2004, Lausanne, Switzerland, p. 175-184, 2004.
PDF.
[LSTM11]
N. Beringer and A. Graves and F. Schiel and J. Schmidhuber. Classifying unprompted speech by retraining LSTM Nets. In W. Duch et al. (Eds.): Proc. Intl. Conf. on Artificial Neural Networks ICANN'05, LNCS 3696, pp. 575-581, Springer-Verlag Berlin Heidelberg, 2005.
[LSTM12]
D. Wierstra, F. Gomez, J. Schmidhuber. Modeling systems with internal state using Evolino. In Proc. of the 2005 conference on genetic and evolutionary computation (GECCO), Washington, D. C., pp. 1795-1802, ACM Press, New York, NY, USA, 2005. Got a GECCO best paper award.
[LSTM13]
F. A. Gers and J. Schmidhuber.
LSTM Recurrent Networks Learn Simple Context Free and
Context Sensitive Languages.
IEEE Transactions on Neural Networks 12(6):1333-1340, 2001.
PDF.
[LSTM14]
S. Fernandez, A. Graves, J. Schmidhuber.
Sequence labelling in structured domains with
hierarchical recurrent neural networks. In Proc.
IJCAI 07, p. 774-779, Hyderabad, India, 2007 (talk).
PDF.
[LSTM15]
A. Graves, J. Schmidhuber.
Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks.
Advances in Neural Information Processing Systems 22, NIPS'22, p 545-552,
Vancouver, MIT Press, 2009.
PDF.
[LSTM16]
M. Stollenga, W. Byeon, M. Liwicki, J. Schmidhuber. Parallel Multi-Dimensional LSTM, With Application to Fast Biomedical Volumetric Image Segmentation. Advances in Neural Information Processing Systems (NIPS), 2015.
Preprint: arxiv:1506.07452.
[LSTM17]
J. A. Perez-Ortiz, F. A. Gers, D. Eck, J. Schmidhuber.
Kalman filters improve LSTM network performance in
problems unsolvable by traditional recurrent nets.
Neural Networks 16(2):241-250, 2003.
PDF.
[LSTM-RL]
B. Bakker, F. Linaker, J. Schmidhuber.
Reinforcement Learning in Partially Observable Mobile Robot
Domains Using Unsupervised Event Extraction.
In Proceedings of the 2002
IEEE/RSJ International Conference on
Intelligent Robots and Systems (IROS 2002), Lausanne, 2002.
PDF.
[LSTMPG]
J. Schmidhuber (AI Blog, Dec 2020). 10-year anniversary of our journal paper on deep reinforcement learning with policy gradients for LSTM (2007-2010). Recent famous applications of policy gradients to LSTM: DeepMind's Starcraft player (2019) and OpenAI's dextrous robot hand & Dota player (2018)—Bill Gates called this a huge milestone in advancing AI.
[META]
J. Schmidhuber (AI Blog, 2020). 1/3 century anniversary of
first publication on metalearning machines that learn to learn (1987).
For its cover I drew a robot that bootstraps itself.
1992-: gradient descent-based neural metalearning. 1994-: Meta-Reinforcement Learning with self-modifying policies. 1997: Meta-RL plus artificial curiosity and intrinsic motivation.
2002-: asymptotically optimal metalearning for curriculum learning. 2003-: mathematically optimal Gödel Machine. 2020: new stuff!
[META1]
J. Schmidhuber.
Evolutionary principles in self-referential learning, or on learning
how to learn: The meta-meta-... hook. Diploma thesis,
Institut für Informatik, Technische Universität München, 1987.
Searchable PDF scan (created by OCRmypdf which uses
LSTM).
HTML.
[For example,
Genetic Programming
(GP) is applied to itself, to recursively evolve
better GP methods through Meta-Evolution.]
[METARL2]
J. Schmidhuber.
On learning how to learn learning strategies.
Technical Report FKI-198-94, Fakultät für Informatik,
Technische Universität München, November 1994.
PDF.
[METARL3]
J. Schmidhuber.
Beyond "Genetic Programming": Incremental Self-Improvement.
In J. Rosca, ed., Proc. Workshop on Genetic Programming at ML95,
pages 42-49. National Resource Lab for the study of Brain and Behavior,
1995.
[METARL4]
M. Wiering and J. Schmidhuber.
Solving POMDPs using Levin search and EIRA.
In L. Saitta, ed.,
Machine Learning:
Proceedings of the 13th International Conference (ICML 1996),
pages 534-542,
Morgan Kaufmann Publishers, San Francisco, CA, 1996.
PDF.
HTML.
[METARL5]
J. Schmidhuber and J. Zhao and M. Wiering.
Simple principles of metalearning.
Technical Report IDSIA-69-96, IDSIA, June 1996.
PDF.
[METARL6]
J. Zhao and J. Schmidhuber.
Solving a complex prisoner's dilemma
with self-modifying policies.
In From Animals to Animats 5: Proceedings
of the Fifth International Conference on Simulation of Adaptive
Behavior, 1998.
[METARL7]
J. Schmidhuber, J. Zhao, and M. Wiering.
Shifting inductive bias with success-story algorithm,
adaptive Levin search, and incremental self-improvement.
Machine Learning 28:105-130, 1997.
PDF.
[METARL8]
J. Schmidhuber, J. Zhao, N. Schraudolph.
Reinforcement learning with self-modifying policies.
In S. Thrun and L. Pratt, eds.,
Learning to learn, Kluwer, pages 293-309, 1997.
PDF;
HTML.
[METARL9]
A general method for incremental self-improvement
and multiagent learning.
In X. Yao, editor, Evolutionary Computation: Theory and Applications.
Chapter 3, pp.81-123, Scientific Publ. Co., Singapore,
1999.
[METARL10]
L. Kirsch, S. van Steenkiste, J. Schmidhuber. Improving Generalization in Meta Reinforcement Learning using Neural Objectives. International Conference on Learning Representations (ICLR), 2020.
[MIR] J. Schmidhuber (AI Blog, Oct 2019, revised 2021). Deep Learning: Our Miraculous Year 1990-1991. Preprint
arXiv:2005.05744, 2020.
The deep learning neural networks of our team have revolutionised pattern recognition and machine learning, and are now heavily used in academia and industry. In 2020-21, we celebrate that many of the basic ideas behind this revolution were published within fewer than 12 months in our "Annus Mirabilis" 1990-1991 at TU Munich.
[MOST]
J. Schmidhuber (AI Blog, 2021). The most cited neural networks all build on work done in my labs. Foundations of the most popular NNs originated in my labs at TU Munich and IDSIA. Here I mention: (1) Long Short-Term Memory (LSTM), (2) ResNet (which is our earlier Highway Net with open gates), (3) AlexNet and VGG Net (both citing our similar earlier DanNet: the first deep convolutional NN to win
image recognition competitions),
(4) Generative Adversarial Networks (an instance of my earlier
Adversarial Artificial Curiosity), and (5) variants of Transformers (linear Transformers are formally equivalent to my earlier Fast Weight Programmers).
Most of this started with our
Annus Mirabilis of 1990-1991.[MIR]
[MOZ]
M. Mozer. A Focused Backpropagation Algorithm for Temporal Pattern Recognition.
Complex Systems, 1989.
[OAI1]
G. Powell, J. Schneider, J. Tobin, W. Zaremba, A. Petron, M. Chociej, L. Weng, B. McGrew, S. Sidor, A. Ray, P. Welinder, R. Jozefowicz, M. Plappert, J. Pachocki, M. Andrychowicz, B. Baker.
Learning Dexterity. OpenAI Blog, 2018.
[OAI1a]
OpenAI, M. Andrychowicz, B. Baker, M. Chociej, R. Jozefowicz, B. McGrew, J. Pachocki, A. Petron, M. Plappert, G. Powell, A. Ray, J. Schneider, S. Sidor, J. Tobin, P. Welinder, L. Weng, W. Zaremba.
Learning Dexterous In-Hand Manipulation. arxiv:1312.5602 (PDF).
[OAI2]
OpenAI:
C. Berner, G. Brockman, B. Chan, V. Cheung, P. Debiak, C. Dennison, D. Farhi, Q. Fischer, S. Hashme, C. Hesse, R. Jozefowicz, S. Gray, C. Olsson, J. Pachocki, M. Petrov, H. P. de Oliveira Pinto, J. Raiman, T. Salimans, J. Schlatter, J. Schneider, S. Sidor, I. Sutskever, J. Tang, F. Wolski, S. Zhang (Dec 2019).
Dota 2 with Large Scale Deep Reinforcement Learning.
Preprint
arxiv:1912.06680.
An LSTM composes 84% of the model's total parameter count.
[OAI2a]
J. Rodriguez. The Science Behind OpenAI Five that just Produced One of the Greatest Breakthrough in the History of AI. Towards Data Science, 2018. An LSTM with 84% of the model's total parameter count was the core of OpenAI Five.
[PIPE]
R. Salustowicz and J. Schmidhuber.
Probabilistic incremental program evolution.
Evolutionary Computation, 5(2):123-141, 1997.
PDF.
[PM0] J. Schmidhuber. Learning factorial codes by predictability minimization. TR CU-CS-565-91, Univ. Colorado at Boulder, 1991. PDF.
More.
[PM1] J. Schmidhuber. Learning factorial codes by predictability minimization. Neural Computation, 4(6):863-879, 1992. Based on [PM0], 1991. PDF.
More.
[PM2] J. Schmidhuber, M. Eldracher, B. Foltin. Semilinear predictability minimzation produces well-known feature detectors. Neural Computation, 8(4):773-786, 1996.
PDF. More.
[PP] J. Schmidhuber.
POWERPLAY: Training an Increasingly General Problem Solver by Continually Searching for the Simplest Still Unsolvable Problem.
Frontiers in Cognitive Science, 2013.
ArXiv preprint (2011):
arXiv:1112.5309 [cs.AI]
[PPa]
R. K. Srivastava, B. R. Steunebrink, M. Stollenga, J. Schmidhuber.
Continually Adding Self-Invented
Problems to the Repertoire: First
Experiments with POWERPLAY.
Proc. IEEE Conference on Development and Learning / EpiRob 2012
(ICDL-EpiRob'12), San Diego, 2012.
PDF.
[PP1] R. K. Srivastava, B. Steunebrink, J. Schmidhuber.
First Experiments with PowerPlay.
Neural Networks, 2013.
ArXiv preprint (2012):
arXiv:1210.8385 [cs.AI].
[PP2] V. Kompella, M. Stollenga, M. Luciw, J. Schmidhuber. Continual curiosity-driven skill acquisition from high-dimensional video inputs for humanoid robots. Artificial Intelligence, 2015.
[R2] Reddit/ML, 2019. J. Schmidhuber really had GANs in 1990.
[R3] Reddit/ML, 2019. NeurIPS 2019 Bengio Schmidhuber Meta-Learning Fiasco.
[R5] Reddit/ML, 2019. The 1997 LSTM paper by Hochreiter & Schmidhuber has become the most cited deep learning research paper of the 20th century.
[RPG]
D. Wierstra, A. Foerster, J. Peters, J. Schmidhuber (2010). Recurrent policy gradients. Logic Journal of the IGPL, 18(5), 620-634.
[RPG07]
D. Wierstra, A. Foerster, J. Peters, J. Schmidhuber. Solving Deep Memory POMDPs
with Recurrent Policy Gradients.
Intl. Conf. on Artificial Neural Networks ICANN'07,
2007.
PDF.
[SOC1]
R. Salustowicz and M. Wiering and J. Schmidhuber.
Evolving soccer strategies.
In N. Kasabov, R. Kozma, K. Ko, R. O'Shea, G. Coghill, and T. Gedeon, editors,
Progress in Connectionist-based Information Systems: Proceedings of the Fourth
International Conference on Neural Information Processing ICONIP'97, volume 1,
pages 502-505, 1997.
PDF.
[SOC2]
R. Salustowicz and M. Wiering and J. Schmidhuber.
Learning team strategies: soccer case studies.
Machine Learning 33(2/3), 263-282, 1998.
.
[SOC3]
M. Wiering and J. Schmidhuber.
CMAC Models Learn to Play Soccer.
In L. Niklasson and M. Boden and T. Ziemke, eds.,
Proceedings of the International Conference on
Artificial Neural Networks, Sweden,
p. 443-448, Springer, London, 1998.
[SOC4]
M. Wiering, R. Salustowicz, J. Schmidhuber.
Reinforcement learning soccer teams
with incomplete world models.
Journal of Autonomous Robots, 7(1):77-88, 1999.
PDF.
[SOC5]
M. Wiering, R. Salustowicz, J. Schmidhuber.
Model-based reinforcement learning for evolving soccer strategies.
In Computational Intelligence in Games, chapter 5. Editors N. Baba
and L. Jain. pp. 99-131, 2001.
PDF.
[STE92]
N. Stephenson (1992). Snow Crash. New York: Bantam Books
[T21]
J. Schmidhuber.
Scientific Integrity, the 2021 Turing Lecture, and the 2018 Turing Award for Deep Learning.
Technical Report IDSIA-77-21, IDSIA, 2021.
[VAN1] S. Hochreiter. Untersuchungen zu dynamischen neuronalen Netzen. Diploma thesis, TUM, 1991 (advisor J. Schmidhuber). PDF.
More on the Fundamental Deep Learning Problem.
[WU] Y. Wu et al. Google's Neural Machine Translation System: Bridging the Gap between Human and Machine Translation.
Preprint arXiv:1609.08144 (PDF), 2016. Based on LSTM which it mentions at least 50 times.
[ZU67]
K. Zuse (1967). Rechnender Raum,
Elektronische Datenverarbeitung,
vol. 8, pages 336-344, 1967.
PDF scan.
[ZU69]
K. Zuse (1969).
Rechnender Raum,
Friedrich Vieweg & Sohn,
Braunschweig, 1969.
English translation:
Calculating Space, MIT Technical Translation AZT-70-164-GEMIT,
MIT (Proj. MAC), Cambridge, Mass. 02139, Feb. 1970.
PDF scan.
[ZUS21]
J. Schmidhuber (AI Blog, 2021). 80th anniversary celebrations: 1941: Konrad Zuse completes the first working general computer, based on his 1936 patent application.
[ZUS21a]
J. Schmidhuber (AI Blog, 2021). 80. Jahrestag: 1941: Konrad Zuse baut ersten funktionalen Allzweckrechner, basierend auf der Patentanmeldung von 1936.
[ZUS21b]
J. Schmidhuber (2021).
Der Mann, der den Computer
erfunden hat. (The man who invented the computer.)
Weltwoche, Nr. 33.21, 19 August 2021.
PDF.
.