 . The variable, real-valued contents
of the work cell with address
. The variable, real-valued contents
of the work cell with address  (later we will encounter additional
instructions):
(later we will encounter additional
instructions):
Storage / Instructions. The learner makes use of an assembler-like
programming language similar to but not quite as general as the one in
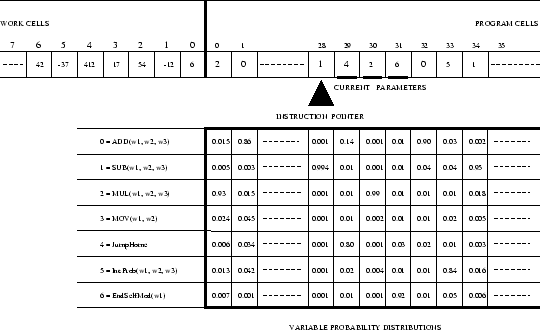
[#!Schmidhuber:95kol!#]. It has ![]() addressable work cells with
addresses ranging from 0 to
addressable work cells with
addresses ranging from 0 to  . The variable, real-valued contents
of the work cell with address
. The variable, real-valued contents
of the work cell with address ![]() are denoted
are denoted ![]() . Processes in the
external environment occasionally write inputs into certain work cells.
There also are
. Processes in the
external environment occasionally write inputs into certain work cells.
There also are ![]() addressable program cells with addresses
ranging from 0 to
addressable program cells with addresses
ranging from 0 to ![]() . The variable, integer-valued contents of
the program cell with address
. The variable, integer-valued contents of
the program cell with address ![]() are denoted
are denoted ![]() . An internal
variable Instruction Pointer (IP) with range
. An internal
variable Instruction Pointer (IP) with range
![]() always points to one of the program cells (initially to the
first one). There also is a fixed set
always points to one of the program cells (initially to the
first one). There also is a fixed set ![]() of
of ![]() integer values
integer values
![]() , which sometimes represent instructions, and
sometimes represent arguments, depending on the position of IP.
IP and work cells together represent the system's internal state
, which sometimes represent instructions, and
sometimes represent arguments, depending on the position of IP.
IP and work cells together represent the system's internal state
![]() (see section 2). For each value
(see section 2). For each value ![]() in
in ![]() , there is an
assembler-like instruction
, there is an
assembler-like instruction ![]() with
with ![]() integer-valued parameters.
In the
following incomplete list of instructions (
integer-valued parameters.
In the
following incomplete list of instructions (
![]() ) to be used
in experiment 3, the symbols
) to be used
in experiment 3, the symbols ![]() stand for parameters that may take on
integer values between
stand for parameters that may take on
integer values between ![]() and
and  (later we will encounter additional
instructions):
(later we will encounter additional
instructions):
Instruction probabilities / Current policy. For each program
cell ![]() there is a variable probability distribution
there is a variable probability distribution ![]() on
on ![]() .
For every possible
.
For every possible ![]() , (
, (
![]() ,
, ![]() specifies for cell
specifies for cell ![]() the conditional probability that, when pointed to
by IP, its contents will be set to
the conditional probability that, when pointed to
by IP, its contents will be set to ![]() . The set of all current
. The set of all current
![]() -values defines a probability matrix
-values defines a probability matrix ![]() with columns
with columns ![]()
![]() .
. ![]() is called the learner's current policy.
In the beginning of the learner's life, all
is called the learner's current policy.
In the beginning of the learner's life, all ![]() are equal (maximum
entropy initialization). If IP
are equal (maximum
entropy initialization). If IP ![]() , the contents of
, the contents of ![]() , namely
, namely
![]() , will be interpreted as instruction
, will be interpreted as instruction ![]() (such as Add
or Mul), and the contents of cells that immediately follow
(such as Add
or Mul), and the contents of cells that immediately follow ![]() will be interpreted as
will be interpreted as ![]() 's arguments, to be selected according
to the corresponding
's arguments, to be selected according
to the corresponding ![]() -values. See Figure 4.
-values. See Figure 4.
Self-modifications. To obtain a learner that can explicitly modify its own policy (by running its own learning strategies), we introduce a special self-modification instruction IncProb not yet mentioned above:
 :
:
In conjunction
with other primitives, ![]() may be used in instruction sequences
that compute directed policy modifications. Calls of
may be used in instruction sequences
that compute directed policy modifications. Calls of ![]() represent
the only way of modifying the policy.
represent
the only way of modifying the policy.
Self-delimiting self-modification sequences (SMSs). SMSs are
subsequences of the lifelong action sequence. The first ![]() after the learner's ``birth'' or after each SSA call (see section
2) begins an SMS. The SMS ends by executing another yet unmentioned
primitive:
after the learner's ``birth'' or after each SSA call (see section
2) begins an SMS. The SMS ends by executing another yet unmentioned
primitive:
Some of the (initially highly random) action subsequences executed during
system life will indeed be SMSs. Depending on the nature of the other
instructions, SMSs can compute almost arbitrary sequences of modifications
of ![]() values. This may result in almost arbitrary modifications of
context-dependent probabilities of future action subsequences, including
future SMSs. Policy changes can be generated only by SMSs. SMSs
build the basis for ``metalearning'': SMSs are generated according to
the policy, and may change the policy. Hence, the policy can essentially
change itself, and also the way it changes itself, etc.
values. This may result in almost arbitrary modifications of
context-dependent probabilities of future action subsequences, including
future SMSs. Policy changes can be generated only by SMSs. SMSs
build the basis for ``metalearning'': SMSs are generated according to
the policy, and may change the policy. Hence, the policy can essentially
change itself, and also the way it changes itself, etc.
SMSs can influence the timing of backtracking processes, because they can influence the times at which the EVALUATION CRITERION will be met. Thus SMSs can temporarily protect the learner from performance evaluations and policy restaurations.
Plugging SMSs into SSA. We replace step 1 in the basic cycle (see section 2) by the following procedure:
We also change step 3 in the SSA cycle as follows: