Jürgen Schmidhuber (2019)
Pronounce: You_again Shmidhoobuh
Twitter: @SchmidhuberAI (inaugural tweet: 4 Oct 2019)
http://people.idsia.ch/~juergen/deep-learning-miraculous-year-1990-1991.html
(Minor edits of May 2020: references added from [DEC] [HIN] / original version here)
Preprint arxiv:2005.05744

The Deep Learning (DL) Neural Networks (NNs) of our team have revolutionised Pattern Recognition and Machine Learning, and are now heavily used in academia and industry [DL4]. In 2020, we will celebrate that many of the basic ideas behind this revolution were published three decades ago within fewer than 12 months in our "Annus Mirabilis" or "Miraculous Year" 1990-1991 at TU Munich. Back then, few people were interested, but a quarter century later, NNs based on these ideas were on over 3 billion devices such as smartphones, and used many billions of times per day, consuming a significant fraction of the world's compute [DL4].

The following summary of what happened in 1990-91 not only contains some high-level context for laymen, but also references for experts who know enough about the field to evaluate the original sources. I also mention selected later work which further developed the ideas of 1990-91 (at TU Munich, the Swiss AI Lab IDSIA, and other places), as well as related work by others. Here the table of contents:

Sec. 0: Background on Deep Learning in Artificial Neural Nets (NNs)
Sec. 1: First Very Deep Learner, Based on Unsupervised Pre-Training (1991)
Sec. 2: Compressing / Distilling one Neural Net into Another (1991)
Sec. 3: The Fundamental Deep Learning Problem (Vanishing / Exploding Gradients, 1991)
Sec. 4: Long Short-Term Memory: Supervised Very Deep Learning (basic insights since 1991)
Sec. 5: Artificial Curiosity Through Adversarial Generative NNs (1990)
Sec. 6: Artificial Curiosity Through NNs that Maximize Learning Progress (1991)
Sec. 7: Adversarial Networks for Unsupervised Data Modeling (1991)
Sec. 8: End-To-End-Differentiable Fast Weights: NNs Learn to Program NNs (1991)
Sec. 9: Learning Sequential Attention with NNs (1990)
Sec. 10: Hierarchical Reinforcement Learning (1990)
Sec. 11: Planning and Reinforcement Learning with Recurrent Neural World Models (1990)
Sec. 12: Goal-Defining Commands as Extra NN Inputs (1990)
Sec. 13: High-Dimensional Reward Signals as NN Inputs / General Value Functions (1990)
Sec. 14: Deterministic Policy Gradients (1990)
Sec. 15: Networks Adjusting Networks / Synthetic Gradients (1990)
Sec. 16: O(n³) Gradient Computation for Online Recurrent NNs (1991)
Sec. 17: The Deep Neural Heat Exchanger (1990)
Sec. 18: My PhD Thesis (1991)
Sec. 19: From Unsupervised Pre-Training to Pure Supervised Learning (1991-95 and 2006-11)
Sec. 20: The Amazing FKI Tech Report Series on Artificial Intelligence in the 1990s
Sec. 21: Concluding Remarks

0. Background on Deep Learning in Neural Nets (NNs)

Most current commercial applications focus on supervised learning to make NNs imitate human teachers [DL1] [DL4]. In the course of many trials, Seppo Linnainmaa's gradient-computing algorithm of 1970 [BP1], today often called backpropagation or the reverse mode of automatic differentiation is used to incrementally weaken certain NN connections and strengthen others, such that the NN behaves more and more like the teacher (compare also [BPA] [BPB] [BP2] [HIN]).

Today's most powerful NNs tend to be very deep, that is, they have many layers of neurons or many subsequent computational stages. In the 1980s, however, gradient-based training did not work well for deep NNs, only for shallow ones [DL1] [DL2].

This Deep Learning Problem was most obvious for recurrent NNs (RNNs, first informally proposed in 1945 [MC43], then formalised in 1956 [K56] - compare [PDA2]). Like the human brain, but unlike the more limited feedforward NNs (FNNs), RNNs have feedback connections. This makes RNNs powerful, general purpose, parallel-sequential computers that can process input sequences of arbitrary length (think of speech or videos). RNNs can in principle implement any program that can run on your laptop. If we want to build an Artificial General Intelligence (AGI), then its underlying computational substrate must be something like an RNN - FNNs are fundamentally insufficient. RNNs relate to FNNs like general computers relate to mere calculators.

In particular, unlike FNNs, RNNs can in principle deal with problems of arbitrary depth [DL1]. Early RNNs of the 1980s, however, failed to learn deep problems in practice. I wanted to overcome this drawback, to achieve RNN-based "general purpose Deep Learning" or "general Deep Learning."

1. First Very Deep NNs, Based on Unsupervised Pre-Training (1991)

My first idea to overcome the Deep Learning Problem mentioned above was to facilitate supervised learning in deep RNNs by unsupervised pre-training of a hierarchical stack of RNNs (1991), to obtain a first "Very Deep Learner" called the Neural Sequence Chunker [UN0] or Neural History Compressor [UN1]. Each higher level minimizes the description length (or negative log probability) of the data representation in the level below, using the Predictive Coding trick: try to predict the next input in the incoming data stream, given the previous inputs, and update neural activations only in case of unpredictable data, thus storing only what's not yet known. In other words, the chunker learns to compress the data stream such that the Deep Learning Problem becomes less severe, and can be solved by standard backpropagation. Although computers back then were about a million times slower per dollar than today, by 1993, my method was able to solve previously unsolvable "Very Deep Learning" tasks of depth > 1000 [UN2] (requiring more than 1,000 subsequent computational stages - the more such stages, the deeper the learning). In 1993, we also published a continuous version of the Neural History Compressor [UN3].

To my knowledge, the Sequence Chunker [UN0] also was the first system made of RNNs operating on different (self-organizing) time scales. (But I also had a way of distilling all those RNNs down into a single deep RNN operating on a single time scale - see Sec. 2.) A few years later, others also started publishing on multi-time scale RNNs, e.g., [HB96]; compare also the Clockwork RNN [CW].

More than a decade after this work [UN1], a similar method for more limited feedforward NNs (FNNs) was published, facilitating supervised learning by unsupervised pre-training of stacks of FNNs called Deep Belief Networks (DBNs) [UN4]. The 2006 justification was essentially the one I used in the early 1990s for my RNN stack: each higher level tries to reduce the description length (or negative log probability) of the data representation in the level below [HIN].

Soon after the unsupervised pre-training-based Very Deep Learner above, the Deep Learning Problem (Sec. 3) was also overcome through our purely supervised LSTM (Sec. 4). Much later, between 2006 and 2011, my lab also drove a very similar shift from unsupervised pre-training to pure supervised learning, two decades after our Miraculous Year, this time for the less general feedforward NNs (FNNs) rather than recurrent NNs (RNNs), with revolutionary applications to cancer detection and many other problems. See Sec. 19 for more on this.

Of course, Deep Learning in feedforward NNs started much earlier, with Ivakhnenko & Lapa, who published the first general, working learning algorithms for deep multilayer perceptrons with arbitrarily many layers back in 1965 [DEEP1]. For example, Ivakhnenko's paper from 1971 [DEEP2] already described a Deep Learning net with 8 layers, trained by a highly cited method still popular in the new millennium [DL2]. But unlike the deep FNNs of Ivakhnenko and his successors of the 1970s and 80s, our deep RNNs had general purpose parallel-sequential computational architectures [UN0-3]. By the early 1990s, most NN research was still limited to rather shallow nets with fewer than 10 subsequent computational stages, while our methods already enabled over 1,000 such stages. I'd say we were the ones who made NNs really deep, especially RNNs, the deepest and most powerful nets of them all.

2. Compressing / Distilling one NN into Another (1991)

My above-mentioned paper on the Neural History Compressor (Sec. 1) also introduced a way of compressing the network hierarchy (whose higher levels are typically running on much slower self-organising time scales than lower levels) into a single deep RNN [UN1] which thus learned to solve very deep problems despite the obstacles mentioned in Sec. 0. This is described in Section 4 of reference [UN1] [DIST1] on a "conscious" chunker and a "subconscious" automatiser, which introduced a general principle for transferring the knowledge of one NN to another. Suppose a teacher NN has learned to predict (conditional expectations of) data, given other data. Its knowledge can be compressed into a student NN, by training the student NN to imitate the behavior of the teacher NN (while also re-training the student NN on previously learned skills such that it does not forget them).

I called this "collapsing" or "compressing" the behavior of one net into another. Today, this is widely used, and also called "distilling" [DIST2] [HIN] or "cloning" the behavior of a teacher net into a student net.

3. The Fundamental Deep Learning Problem: Vanishing / Exploding Gradients (1991)

As a part of his thesis, Sepp implemented the Neural History Compressor above (Sec. 1) and other RNN-based systems (Sec. 11). However, he did much more: His work formally showed that deep NNs suffer from the now famous problem of vanishing or exploding gradients: in typical deep or recurrent networks, back-propagated error signals either shrink rapidly, or grow out of bounds. In both cases, learning fails. This analysis led to basic principles of what's now called LSTM (Sec. 4).

(In 1994, others published results [VAN2] essentially identical to the 1991 vanishing gradient results of Sepp [VAN1]. Even after a common publication [VAN3], the first author of reference [VAN2] published papers (e.g., [VAN4]) that cited only his own 1994 paper but not Sepp's original work.)

Note that Sepp's thesis identified those problems of backpropagation in deep NNs two decades after another student with a similar first name (Seppo Linnainmaa) published modern backpropagation or the reverse mode of automatic differentiation in his own thesis of 1970 [BP1].

4. Long Short-Term Memory (LSTM) Recurrent Networks: Supervised Very Deep Learning

In 2020 we'll celebrate the quarter-century anniversary of LSTM's first failure to pass peer review. After the main peer-reviewed publication in 1997 [LSTM1] (now the most cited article in the history of Neural Computation), LSTM and its training procedures were further improved on my Swiss LSTM grants at IDSIA through the work of my later students Felix Gers, Alex Graves, and others. A milestone was the "vanilla LSTM architecture" with forget gate [LSTM2] - the LSTM variant of 1999-2000 that everybody is using today, e.g., in Google's Tensorflow. The LSTM forget gate is actually an end-to-end differentiable fast weight controller of the type we also introduced in 1991 [FAST0] (Sec. 8).

Alex was lead author of our first successful application of LSTM to speech (2004) [LSTM10]. 2005 saw the first publication of LSTM with full backpropagation through time and of bi-directional LSTM [LSTM3] (now widely used). Another milestone of 2006 was the training method "Connectionist Temporal Classification" or CTC [CTC] for simultaneous alignment and recognition of sequences. Our team successfully applied CTC-trained LSTM to speech in 2007 [LSTM4] (also with hierarchical LSTM stacks [LSTM14]). This was the first superior end-to-end neural speech recognition. It was very different from hybrid methods since the late 1980s which combined NNs and traditional approaches such as Hidden Markov Models (HMMs), e.g., [BW] [BRI] [BOU] [HYB12]. In 2015, the CTC-LSTM combination dramatically improved Google's speech recognition on the Android smartphones [GSR15] [DL4].

The first superior end-to-end neural machine translation was also based on our LSTM. In 1995, we already had an excellent neural probabilistic text model [SNT]. In the early 2000s, we showed how LSTM can learn languages unlearnable by traditional models such as Hidden Markov Models [LSTM13]. This took a while to sink in, and compute still had to get 1000 times cheaper, but by 2016-17, both Google Translate [WU] [GT16] and Facebook Translate [FB17] were based on two connected LSTMs [S2S], one for the incoming text, one for the outgoing translation, much better than what they had before [DL4].

In 2009, my PhD student Justin Bayer was lead author of a system that automatically designed LSTM-like architectures outperforming vanilla LSTM in certain applications [LSTM7]. In 2017, Google started using similar "neural architecture search" [NAS].

Since 2006, we have worked with the software industry (e.g., LifeWare) to greatly improve handwriting recognition. In 2009, through the efforts of Alex, LSTM trained by CTC became the first RNN to win international competitions, namely, three ICDAR 2009 Connected Handwriting Competitions (French, Farsi, Arabic). This attracted enormous interest from industry. LSTM was soon used for everything that involves sequential data such as language and speech [LSTM10-11] [LSTM4] [DL1] and videos. By 2017, LSTM powered Facebook's machine translation (over 30 billion translations per week) [FB17] [DL4], Apple's Quicktype on roughly 1 billion iPhones [DL4], the voice of Amazon's Alexa [DL4], Google's speech recognition (on Android smartphones since 2015) [GSR15] [DL4] & image caption generation [DL4] & machine translation [GT16] [DL4] & automatic email answering [DL4], etc. Business Week called LSTM "arguably the most commercial AI achievement" [AV1].

By 2016, more than a quarter of the awesome computational power for inference in Google's datacenters was used for LSTM (and 5% for another popular Deep Learning technique called CNNs - see Sec. 19) [JOU17]. Google's new on-device speech recognition of 2019 (now on your phone, not on the server) is still based on LSTM.

Through the work of my students Rupesh Kumar Srivastava and Klaus Greff, the LSTM principle also led to our Highway Networks [HW1] of May 2015, the first working very deep FNNs with hundreds of layers. Microsoft's popular ResNets [HW2] (which won the ImageNet 2015 contest) are a special case thereof. The earlier Highway Nets perform roughly as well as ResNets on ImageNet [HW3]. Highway layers are also often used for natural language processing, where the simpler residual layers do not work as well [HW3].

We also trained LSTM through Reinforcement Learning (RL) for robotics without a teacher, e.g., with my postdoc Bram Bakker [LSTM-RL] (2002). And also through Neuroevolution and policy gradients, e.g., with my PhD student Daan Wierstra [LSTM12] [RPG], who later became employee number 1 of DeepMind, the company co-founded by his friend Shane Legg, another PhD student from my lab (Shane and Daan were the first persons at DeepMind with AI publications and PhDs in computer science). RL with LSTM has become important. For example, in 2019, DeepMind beat a pro player in the game of Starcraft, which is harder than Chess or Go [DM2] in many ways, using Alphastar whose brain has a deep LSTM core trained by RL [DM3]. An RL LSTM (with 84% of the model's total parameter count) also was the core of the famous OpenAI Five which learned to defeat human experts in the Dota 2 video game (2018) [OAI2]. Bill Gates called this a "huge milestone in advancing artificial intelligence" [OAI2a]. See [MIR], Sec. 4.

Essential foundations for all of this were laid in 1991. My team subsequently developed LSTM & CTC etc. with the help of basic funding from TU Munich and the (back then private) Swiss Dalle Molle Institute for AI (IDSIA), as well as public funding which I acquired from Switzerland & Germany & EU during the "Neural Network Winter" of the 1990s and early 2000s, trying to keep the field alive when few were interested in NNs. I am especially thankful to Professors Kurt Bauknecht & Leslie Kaelbling & Ron Williams & Ray Solomonoff whose positive reviews of my grant proposals have greatly helped to obtain financial support from SNF since the 1990s.

5. Artificial Curiosity Through Adversarial Generative NNs (1990)

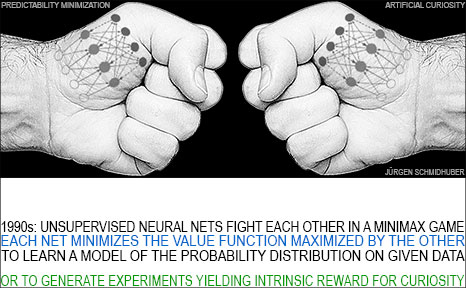
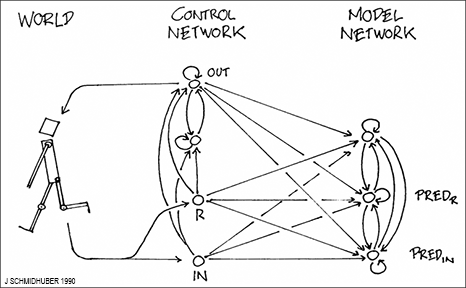
How does Adversarial Curiosity work? The first NN is called the controller C. C (probabilistically) generates outputs that may influence an environment. The second NN is called the world model M. It predicts the environmental reactions to C's outputs. Using gradient descent, M minimizes its error, thus becoming a better predictor. But in a zero sum game, C tries to find outputs that maximize the error of M. M's loss is the gain of C.

That is, C is motivated to invent novel outputs or experiments that yield data that M still finds surprising, until the data becomes familiar and eventually boring. Compare more recent summaries and extensions of this principle, e.g., [AC09].

So in 1990 we already had unsupervised or self-supervised neural nets that were both generative and adversarial (using much later terminology from 2014 [GAN1]), generating experimental outputs yielding novel data, not only for stationary patterns but also for pattern sequences, and even for the general case of Reinforcement Learning (RL).

The popular Generative Adversarial Networks (GANs) [GAN0] [GAN1] (2010-2014) are an application of Adversarial Curiosity [AC90] where the environment simply returns whether C's current output is in a given set [AC19] [AC20].

BTW, note that the closely related Adversarial Curiosity [AC90, AC90b] & GANs [GAN0, GAN1] & Adversarial Predictability Minimization (Sec. 7) are very different from other early adversarial machine learning settings [GS59] [H90] which neither involved unsupervised NNs nor were about modeling data nor used gradient descent [AC20].

6. Artificial Curiosity Through NNs That Maximize Learning Progress (1991)

The errors of AC1990's world model M (to be minimized, Sec. 5) are the rewards of the controller C (to be maximized). This makes for a fine exploration strategy in many deterministic environments. In stochastic environments, however, this might fail. C might learn to focus on situations where M can always get high prediction errors due to randomness, or due to its computational limitations. For example, an agent controlled by C might get stuck in front of a TV screen showing highly unpredictable white noise [AC10].

Therefore, as pointed out in 1991, in stochastic environments, C's reward should not be the errors of M, but (an approximation of) the first derivative of M's errors across subsequent training iterations, that is, M's improvements [AC91] [AC91b]. As a consequence, despite its high errors in front of the noisy TV screen above, C won't get rewarded for getting stuck there. Both the totally predictable and the fundamentally unpredictable will get boring. This insight led to lots of follow-up work [AC10] on artificial scientists and artists, e.g., [AC09].

7. Adversarial Networks for Unsupervised Data Modeling (1991)

Soon after my first work on adversarial generative networks in 1990 (Sec. 5), I introduced a variation of the unsupervised adversarial minimax principle while I was a postdoc at the University of Colorado at Boulder. One of the most important NN tasks is to learn the statistics of given data such as images. To achieve this, I used again the principles of gradient descent/ascent in a minimax game where one NN minimizes the objective function maximized by another. This duel between two unsupervised adversarial NNs was called Predictability Minimization (PM, 1990s) [PM2] [PM1] [PM0]. (Contrary to later claims [GAN1], PM is indeed a pure minimax game, e.g., [PM2], Equation 2. Compare the survey [AC20].)

The first toy experiments with PM [PM1] were conducted nearly three decades ago when compute was about a million times more expensive than today. When it had become about 10 times cheaper 5 years later, we could show that semi-linear PM variants applied to images automatically generate feature detectors well-known from neuroscience, such as on-center-off-surround detectors, off-center-on-surround detectors, and orientation-sensitive bar detectors [PM2].

8. End-To-End-Differentiable Fast Weights: NNs Learn to Program NNs (1991)

Dynamic links or fast weights for NNs were introduced by Christoph v. d. Malsburg in 1981 [FAST] and further studied by others, e.g., [FASTb]. However, these authors did not have an end-to-end-differentiable system that learns by gradient descent to quickly manipulate the fast weight storage. Such a system I published in 1991 [FAST0] [FAST1]. There a slow NN learns to control the weights of a separate fast NN. That is, I separated storage and control like in traditional computers, but in a fully neural way (rather than in a hybrid fashion [PDA1] [PDA2] [DNC]). This led to lots of follow-up work, some of it mentioned below.

One year later, I introduced gradient descent-based, active control of fast weights through 2D tensors or outer product updates [FAST2] (compare our more recent work on this [FAST3] [FAST3a]). The motivation was to get many more temporal variables under end-to-end differentiable control than what's possible in standard RNNs of the same size: O(H^2) instead of O(H), where H is the number of hidden units. A quarter century later, others followed this approach [FAST4a]. The paper [FAST2] also explicitly addressed the learning of "internal spotlights of attention" in end-to-end-differentiable networks. Compare Sec. 9 on learning attention.

I also showed how fast weights can be used for meta-learning or "learning to learn", one of my main research topics since 1987 [META1]. In references [FASTMETA1-3] since 1992, the slow RNN and the fast RNN are identical: the initial weight of each connection in the net is trained by gradient descent, but during an episode, each connection can be addressed and read and modified by the net itself (through O(log n) special output units where n is the number of connections), and the connection's weight may rapidly change - the network becomes self-referential in the sense that it can in principle learn to run arbitrary computable weight change algorithms or learning algorithms (for all of its weights) on itself. This led to many follow-up papers in the 1990s and 2000s.

Deep Reinforcement Learning (RL) without a teacher can also profit from fast weights even when the system's dynamics are not differentiable, as shown in 2005 by my former postdoc Faustino Gomez [FAST5] (now CEO of NNAISENSE) when affordable computers were about 1000 times faster than in the early 1990s.

BTW, our related work on Deep RL in the same year (but without fast weights) to my knowledge was the first machine learning publication with the word combination "learn deep" in the title [DL6] (2005; soon afterwards many started talking about "deep learning").

Over the decades we have published quite a few additional ways of learning to generate quickly numerous weights of large NNs through very compact codes, e.g., [KO0] [KO1] [KO2] [CO1] [CO2] [CO3]. Here we exploited that the Kolmogorov complexity or algorithmic information content of successful huge NNs may actually be rather small. In particular, in July 2013, "Compressed Network Search" [CO2] was the first deep learning model to successfully learn control policies directly from high-dimensional sensory input (video) using reinforcement learning, without any unsupervised pre-training (unlike in Sec. 1). Soon afterwards, DeepMind also had a Deep RL system for high-dimensional sensory input [DM1] [DM2].

Today, the most famous end-to-end differentiable fast weight-based NN [FAST0] is actually our vanilla LSTM network of 2000 [LSTM2] (Sec. 4), whose forget gates learn to control the fast weights on self-recurrent connections of internal LSTM cells. All the major IT companies are now massively using vanilla LSTM [DL4]. Again, the roots of this go back to 1991 (Sec. 4 & Sec. 8).

9. Learning Sequential Attention with NNs (1990)

So back then we already had both of the now common types of neural sequential attention: end-to-end-differentiable "soft" attention (in latent space) through multiplicative units within NNs [FAST2], and "hard" attention (in observation space) in the context of Reinforcement Learning (RL) [ATT0] [ATT1]. This led to lots of follow-up work. Today, many are using sequential attention-learning NNs.

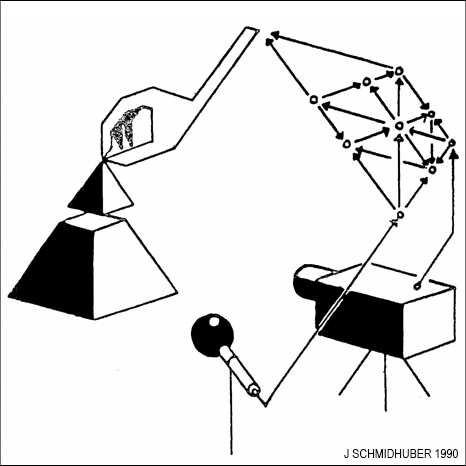
My overview paper for CMSS 1990 [ATT2] summarised in Section 5 our early work on attention, to my knowledge the first implemented neural system for combining glimpses that jointly trains a recognition & prediction component with an attentional component (the fixation controller). Two decades later, the reviewer of my 1990 paper wrote about his own work as second author of a related paper [ATT3]: "To our knowledge, this is the first implemented system for combining glimpses that jointly trains a recognition component ... with an attentional component (the fixation controller)." Compare Sec. 10.

10. Hierarchical Reinforcement Learning (1990)

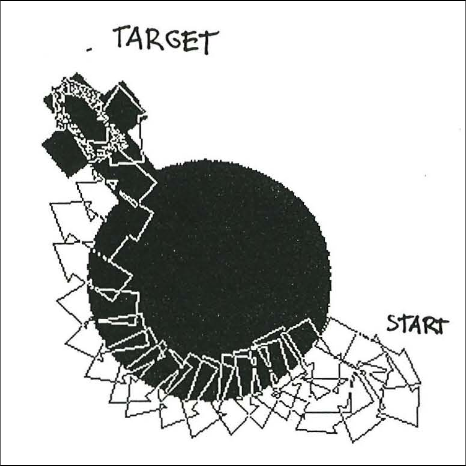
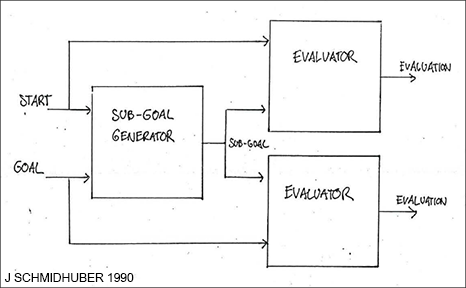
Our 1990-91 papers [HRL0] [HRL1] were the first of many follow-up papers on HRL, e.g., [HRL4]. Soon afterwards, others also started publishing on HRL. For example, the reviewer of our reference [ATT2] (which summarised in Section 6 our early work on HRL) was last author of ref [HRL3]. Compare Sec. 9.

11. Planning with Recurrent Neural World Models (1990)

The 1990 FKI report [AC90] also introduced several other concepts that have become popular. See Sec. 12, Sec. 13, Sec. 14, Sec. 5, Sec. 20.

12. Goal-Defining Commands as Extra NN Inputs (1990)

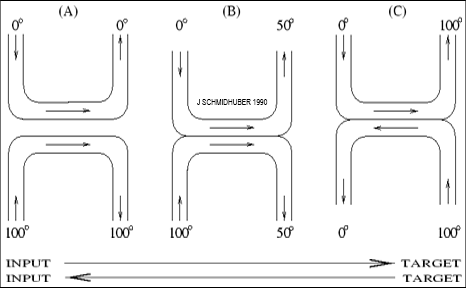
One concept that is widely used in today's RL NNs are extra goal-defining input patterns that encode various tasks, such that the NN knows which task to execute next. We introduced this in 1990 in various contexts [ATT0] [ATT1] [HRL0] [HRL1]. In references [ATT0] [ATT1], a reinforcement learning neural controller learned to control a fovea through sequences of saccades to find particular objects in visual scenes, thus learning sequential attention (Sec. 9). User-defined goals were provided to the system by special "goal input vectors" that remained constant (Sec. 3.2 of [ATT1]) while the system shaped its stream of visual inputs through fovea-shifting actions.

Hierarchical RL (HRL, Sec. 10) with end-to-end differentiable subgoal generators [HRL0] [HRL1] also uses an NN with task-defining inputs of the form (start, goal), learning to predict the costs of going from start to goal. (Compare my former student Tom Schaul's "universal value function approximator" at DeepMind a quarter century later [UVF15].)

This led to lots of follow-up work. For example, our POWERPLAY RL system (2011) [PP] [PP1] also uses task-defining inputs to distinguish between tasks, continually inventing on its own new goals and tasks, incrementally learning to become a more and more general problem solver in an active, partially unsupervised or self-supervised fashion. RL robots with high-dimensional video inputs and intrinsic motivation (like in PowerPlay) learned to explore in 2015 [PP2].

13. High-Dimensional Reward Signals As NN Inputs / General Value Functions (1990)

Traditional RL is based on one-dimensional reward signals. Humans, however, have millions of informative sensors for different types of pain and pleasure etc. To my knowledge, reference [AC90] was the first paper on RL with multi-dimensional, vector-valued pain and reward signals coming in through many different sensors, where cumulative values are predicted for all those sensors, not just for a single scalar overall reward. Compare what was later called a general value function [GVF]. Unlike previous adaptive critics, the one of 1990 [AC90] was multi-dimensional and recurrent.

Unlike in traditional RL, those reward signals were also used as informative inputs to the controller NN learning to execute actions that maximise cumulative reward.

14. Deterministic Policy Gradients (1990)

15. Networks Adjusting Networks / Synthetic Gradients (1990)

Unlike standard backpropagation, the method is local in space and time [BB1] [NAN1]. A quarter century later, DeepMind called this "Synthetic Gradients" [NAN5].

16. O(n³) Gradients for Online Recurrent NNs (1991)

BTW, I committed a similar error in 1987 when I published what I thought was the first paper on Genetic Programming (GP), that is, on automatically evolving computer programs [GP1] (authors in alphabetic order). Only later I found out that Nichael Cramer had published GP already in 1985 [GP0] (and that Stephen F. Smith had proposed a related approach as part of a larger system [GPA] in 1980). Since then I have been trying to do the right thing and correctly attribute credit. At least our 1987 paper [GP1] seems to be the first on GP for codes with loops and codes of variable size, and the first on GP implemented in a Logic Programming language.

17. The Deep Neural Heat Exchanger (1990)

18. PhD Thesis (1990)

Back then, much of the NN research by others was inspired by statistical mechanics, e.g., [HOP]. The works of 1990-91 (and my even earlier diploma thesis of 1987 [META1]) embodied an alternative program-oriented view of Machine Learning.

When Kurt Gödel founded theoretical computer science in 1931 [GOD], he represented both data (such as axioms and theorems) and programs (such as proof-generating sequences of operations on the data) in a universal coding language based on the integers. He famously used this language to construct formal statements that talk about the computation of other formal statements, especially self-referential formal statements which state that they are not provable by any computational theorem prover. Thus he exhibited the fundamental limits of mathematics and computation and Artificial Intelligence.

As I have frequently pointed out since 1990 [AC90], the weights of an NN should be viewed as its program. Some argue that the goal of a deep NN is to learn useful internal representations of observed data (there even is an international conference on learning representations called ICLR), but I have always preferred the view that the NN's goal is actually to learn a program (the parameters) that computes such representations. Inspired by Gödel, I built NNs whose outputs are programs or weight matrices of other NNs (Sec. 8), and even self-referential RNNs that can run and inspect their own weight change algorithms or learning algorithms (Sec. 8). A difference to Gödel's work is that the universal programming language is not based on the integers, but on real values, such that the outputs of typical NNs are differentiable with respect to their programs. That is, a simple program generator (the efficient gradient descent procedure [BP1]) can compute a direction in program space where one may find a better program [AC90], in particular, a better program-generating program (Sec. 8). Much of my work since 1989 has exploited this fact.

19. From Unsupervised Pre-Training to Pure Supervised Learning (1991-95 and 2006-11)

As mentioned in Sec. 1, my first Very Deep Learner was the RNN stack of 1991 which used unsupervised pre-training to learn problems of depth greater than 1000. Soon afterwards, however, we published more general ways of overcoming the Deep Learning Problem (Sec. 3) without any unsupervised pre-training, replacing the unsupervised RNN stack [UN1-3] by the purely supervised Long Short-Term Memory (LSTM) (Sec. 4). That is, already in the previous millennium, unsupervised pre-training lost significance as LSTM did not require it. In fact, this shift from unsupervised pre-training to pure supervised learning started already in 1991.

A very similar shift took place much later between 2006 and 2010, this time for the less general feedforward NNs (FNNs) rather than recurrent NNs (RNNs). Again, my little lab played a central role in this transition. In 2006, supervised learning in FNNs was facilitated by unsupervised pre-training of stacks of FNNs [UN4] (Sec. 1). But in 2010, our team with my outstanding Romanian postdoc Dan Ciresan [MLP1] showed that deep FNNs can be trained by plain backpropagation and do not at all require unsupervised pre-training for important applications [DEC]. Our system set a new performance record [MLP1] on the back then famous and widely used image recognition benchmark called MNIST. This was achieved by greatly accelerating traditional FNNs on highly parallel graphics processing units called GPUs. A reviewer called this a "wake-up call to the machine learning community." Today, very few commercial DL applications are still based on unsupervised pre-training.

My team at the Swiss AI Lab IDSIA further improved the above-mentioned work (2010) on purely supervised Deep Learning in FNNs [MLP1] by replacing the traditional FNNs through another old NN type called convolutional NNs or CNNs, invented and developed by others since the 1970s [CNN1-4]. Our supervised ensemble of fast GPU-based CNNs (Ciresan et al., 2011) [GPUCNN1] was a practical breakthrough (much faster than early work on accelerating CNNs [GPUCNN]) and won 4 important computer vision competitions in a row between May 15, 2011, and September 10, 2012 [GPUCNN5]. (All of this happened before a similar GPU-CNN by others won ImageNet 2012 [GPUCNN5].) In particular, our fast deep CNNs were the first to win a Chinese handwriting contest (ICDAR 2011), the first to achieve superhuman visual pattern recognition in any international contest (IJCNN 2011), the first to win an image segmentation contest (ISBI, May 2012), and the first to win a contest on object detection in large images (ICPR, 10 Sept 2012), at the same time the first to win a medical imaging contest [GPUCNN5] (on cancer detection). One year later, our team also won the MICCAI Grand Challenge on mitosis detection [MGC] [GPUCNN5] [GPUCNN8]. Our fast CNN image scanners were over 1000 times faster than previous methods [SCAN]. This deep learning approach has transformed medical imaging.

Our system more than halved the error rate for object recognition in a contest already in 2011, 20 years after our Annus Mirabilis [GPUCNN2]. Soon afterwards, others applied similar approaches in image recognition contests [GPUCNN5].

Like our LSTM results of 2009 (Sec. 4), the above-mentioned results with feedforward NNs of 2010-11 attracted enormous interest from industry. For example, in 2010, we introduced our deep and fast GPU-based NNs to Arcelor Mittal, the world's largest steel maker, and were able to greatly improve steel defect detection [ST]. This may have been the first Deep Learning breakthrough in heavy industry. Today, most AI startups and major IT firms as well as many other famous companies are using such supervised fast GPU-NNs.

20. The Amazing FKI Tech Report Series on Artificial Intelligence in the 1990s

Most of the results above were actually first published in TU Munich's FKI Tech Report series, for which I drew many illustrations by hand, some of them shown in the present page (Sec. 10, Sec. 11, Sec. 13, Sec. 18). The FKI series now plays an important role in the history of Artificial Intelligence, as it introduced several important concepts: Unsupervised Pre-Training for Very Deep Learning (FKI-148-91 [UN0], Sec. 1), Compressing / Distilling one NN into Another (FKI-148-91 [UN0], Sec. 2), Long Short-Term Memory (FKI-207-95 [LSTM0], Sec. 4, see also Sec. 8), Artificial Curiosity Through NNs that Maximize Learning Progress (FKI-149-91 [AC91], Sec. 6), End-To-End-Differentiable Fast Weights and NNs that learn to program other NNs (separating storage and control for NNs like in traditional computers, FKI-147-91 [FAST0], Sec. 8), Learning of Sequential Attention with NNs (FKI-128-90 [ATT0], Sec. 9), Goal-Defining Commands as Extra NN Inputs (FKI-128-90 [ATT0], FKI-129-90 [HRL0], Sec. 12), Hierarchical Reinforcement Learning (FKI-129-90 [HRL0], Sec. 10), Networks Adjusting Networks / Synthetic Gradients (FKI-125-90 [NAN2], Sec. 15). (Cubic Gradient Computation for Online Recurrent NNs also was published as FKI-151-91 [CUB1], but this one does not really count, see Sec. 16.) In particular, the report FKI-126-90 [AC90] introduced a whole bunch of concepts that are now widely used: Planning with Recurrent World Models (Sec. 11), High-Dimensional Reward Signals as Extra NN Inputs / General Value Functions (Sec. 13), Deterministic Policy Gradients (Sec. 14), NNs that are both Generative and Adversarial (Sec. 5; see also Sec. 7), for Artificial Curiosity and related concepts. Later remarkable FKI Tech Reports from the 1990s describe ways of greatly compressing NNs [KO0] [FM] to improve their generalisation capability.

Peer-reviewed versions came out soon after the tech reports. For example, in 1992, I had a fun contest with the great David MacKay as to who'd have more publications within a single year in Neural Computation, back then the leading journal of our field. By the end of 1992, both of us had four. But David won, because his publications (mostly on Bayesian approaches for NNs) were much longer than mine :-) Disclaimer: Of course, silly measures like number of publications and h-index etc should not matter in science - the only thing that really counts is research quality [NAT1].

21. Concluding Remarks

In surveys from the Anglosphere it does not always become clear [DLC] that Deep Learning was invented where English is not an official language. It started in 1965 in the Ukraine (back then the USSR) with the first nets of arbitrary depth that really learned [DEEP1-2] (Sec. 1). Five years later, modern backpropagation was published "next door" in Finland (1970) [BP1] (Sec. 0). The basic deep convolutional NN architecture (now widely used) was invented in the 1970s in Japan [CNN1], where NNs with convolutions were later (1987) also combined with "weight sharing" and backpropagation [CNN1a]. Unsupervised or self-supervised adversarial networks that duel each other in a minimax game for Artificial Curiosity etc (now widely used) originated in Munich (1990, Sec. 5) (also the birthplace of the first truly self-driving cars in the 1980s - in highway traffic by 1994). The Fundamental Problem of Backpropagation-Based Deep Learning (1991, Sec. 3) [VAN1] was also discovered in Munich. So were the first "modern" Deep Learners to overcome this problem, through (1) unsupervised pre-training [UN1-2] (1991, Sec. 1), and (2) Long Short-Term Memory [LSTM0-7], "arguably the most commercial AI achievement" [AV1] (Sec. 4). LSTM was further developed in Switzerland (Sec. 4), which is also home of the first image recognition contest-winning deep GPU-based CNNs (2011, Sec. 19 - everybody in computer vision is using this approach now), the first superhuman visual pattern recognition (2011), and the first very deep, working feedforward NNs with more than a hundred layers [HW1] (Sec. 4). Around 1990, Switzerland also became origin of the World Wide Web, which allowed for quickly spreading AI around the globe. As of 2017, Switzerland is still leading the world in AI research in terms of citation impact, although China is now the nation that produces the most papers on AI [THE17].

Of course, Deep Learning is just a small part of AI, mostly limited to passive pattern recognition. We view it as a by-product of our research on more general AI through meta-learning or "learning to learn learning algorithms" (publications since 1987), systems with artificial curiosity and creativity that invent their own problems and set their own goals (since 1990), evolutionary computation (since 1987) & RNN evolution & compressed network search, reinforcement learning (RL) for agents in realistic partially observable environments where traditional RL (for board games etc) does not work (since 1989), general artificial intelligence, optimal universal learning machines such as the Gödel machine (2003-), optimal search for programs running on general purpose computers such as RNNs, etc.

And of course, AI itself is just part of a grander scheme driving the universe from simple initial conditions to more and more unfathomable complexity [SA17]. Finally, even this awesome process may be just a tiny part of the even grander, optimally efficient computation of all logically possible universes [ALL1] [ALL2] [ALL3].

Acknowledgments

Thanks to several expert reviewers for useful comments. (Let me know under juergen@idsia.ch if you can spot any remaining error.) The contents of this article may be used for educational and non-commercial purposes, including articles for Wikipedia and similar sites.

References

[DL1] J. Schmidhuber, 2015. Deep Learning in neural networks: An overview. Neural Networks, 61, 85-117. More.

[DL2] J. Schmidhuber, 2015. Deep Learning. Scholarpedia, 10(11):32832.

[DL4] J. Schmidhuber, 2017. Our impact on the world's most valuable public companies: 1. Apple, 2. Alphabet (Google), 3. Microsoft, 4. Facebook, 5. Amazon ... HTML.

[DLC] J. Schmidhuber, 2015. Critique of Paper by "Deep Learning Conspiracy" (Nature 521 p 436). June 2015. HTML.

[DL6] F. Gomez and J. Schmidhuber. Co-evolving recurrent neurons learn deep memory POMDPs. In Proc. GECCO'05, Washington, D. C., pp. 1795-1802, ACM Press, New York, NY, USA, 2005. PDF.

[AV1] A. Vance. Google Amazon and Facebook Owe Jürgen Schmidhuber a Fortune - This Man Is the Godfather the AI Community Wants to Forget. Business Week, Bloomberg, May 15, 2018.

[MC43] W. S. McCulloch, W. Pitts. A Logical Calculus of Ideas Immanent in Nervous Activity. Bulletin of Mathematical Biophysics, Vol. 5, p. 115-133, 1943.

[K56] S.C. Kleene. Representation of Events in Nerve Nets and Finite Automata. Automata Studies, Editors: C.E. Shannon and J. McCarthy, Princeton University Press, p. 3-42, Princeton, N.J., 1956.

[ROB] A. J. Robinson and F. Fallside. The utility driven dynamic error propagation network. Technical Report CUED/F-INFENG/TR.1, Cambridge University Engineering Department, 1987.

[CUB0] R. J. Williams. Complexity of exact gradient computation algorithms for recurrent neural networks. Technical Report NU-CCS-89-27, Northeastern University, College of Computer Science, 1989.

[CUB1] An O(n³) learning algorithm for fully recurrent neural networks. Technical Report FKI-151-91, Institut für Informatik, Technische Universität München, 1991. PDF.

[CUB2] J. Schmidhuber. A fixed size storage O(n³) time complexity learning algorithm for fully recurrent continually running networks. Neural Computation, 4(2):243-248, 1992. PDF.

[GPA] S. F. Smith. A Learning System Based on Genetic Adaptive Algorithms, PhD Thesis, Univ. Pittsburgh, 1980.

[GP0] N. Cramer. A Representation for the Adaptive Generation of Simple Sequential Programs, Proc. of an Intl. Conf. on Genetic Algorithms and their Applications, Carnegie-Mellon University, July 24-26, 1985.

[GP1] D. Dickmanns, J. Schmidhuber, and A. Winklhofer. Der genetische Algorithmus: Eine Implementierung in Prolog. Fortgeschrittenenpraktikum, Institut für Informatik, Lehrstuhl Prof. Radig, Technische Universität München, 1987. HTML.

[NHE] J. Schmidhuber. The Neural Heat Exchanger. Oral presentations since 1990 at various universities including TUM and the University of Colorado at Boulder. Also in In S. Amari, L. Xu, L. Chan, I. King, K. Leung, eds., Proceedings of the Intl. Conference on Neural Information Processing (1996), pages 194-197, Springer, Hongkong. Link.

[HEL] P. Dayan, G. E. Hinton, R. M. Neal, and R. S. Zemel. The Helmholtz machine. Neural Computation, 7:889-904, 1995.

[ATT0] J. Schmidhuber and R. Huber. Learning to generate focus trajectories for attentive vision. Technical Report FKI-128-90, Institut für Informatik, Technische Universität München, 1990. PDF.

[ATT1] J. Schmidhuber and R. Huber. Learning to generate artificial fovea trajectories for target detection. International Journal of Neural Systems, 2(1 & 2):135-141, 1991. Based on TR FKI-128-90, TUM, 1990. PDF. More.

[ATT2] J.  Schmidhuber. Learning algorithms for networks with internal and external feedback. In D. S. Touretzky, J. L. Elman, T. J. Sejnowski, and G. E. Hinton, editors, Proc. of the 1990 Connectionist Models Summer School, pages 52-61. San Mateo, CA: Morgan Kaufmann, 1990. PS. (PDF.)

[ATT3] H. Larochelle, G. E. Hinton. Learning to combine foveal glimpses with a third-order Boltzmann machine. NIPS 2010.

[HRL0] J.  Schmidhuber. Towards compositional learning with dynamic neural networks. Technical Report FKI-129-90, Institut für Informatik, Technische Universität München, 1990. PDF.

[HRL1] J. Schmidhuber. Learning to generate sub-goals for action sequences. In T. Kohonen, K. Mäkisara, O. Simula, and J. Kangas, editors, Artificial Neural Networks, pages 967-972. Elsevier Science Publishers B.V., North-Holland, 1991. PDF. Extending TR FKI-129-90, TUM, 1990. HTML & images in German.

[HRL2] J.  Schmidhuber and R. Wahnsiedler. Planning simple trajectories using neural subgoal generators. In J. A. Meyer, H. L. Roitblat, and S. W. Wilson, editors, Proc. of the 2nd International Conference on Simulation of Adaptive Behavior, pages 196-202. MIT Press, 1992. PDF. HTML & images in German.

[HRL3] P. Dayan and G. E. Hinton. Feudal Reinforcement Learning. Advances in Neural Information Processing Systems 5, NIPS, 1992.

[HRL4] M. Wiering and J. Schmidhuber. HQ-Learning. Adaptive Behavior 6(2):219-246, 1997. PDF.

[UVF15] T. Schaul, D. Horgan, K. Gregor, D. Silver. Universal value function approximators. Proc. ICML 2015, pp. 1312-1320, 2015.

[UN0] J.  Schmidhuber. Neural sequence chunkers. Technical Report FKI-148-91, Institut für Informatik, Technische Universität München, April 1991. PDF.

[UN1] J. Schmidhuber. Learning complex, extended sequences using the principle of history compression. Neural Computation, 4(2):234-242, 1992. Based on TR FKI-148-91, TUM, 1991 [UN0]. PDF. [First working Deep Learner based on a deep RNN hierarchy, overcoming the vanishing gradient problem. Also: compressing or distilling a teacher net (the chunker) into a student net (the automatizer) that does not forget its old skills - such approaches are now widely used. More.]

[UN2] J. Schmidhuber. Habilitation thesis, TUM, 1993. PDF. [An ancient experiment on "Very Deep Learning" with credit assignment across 1200 time steps or virtual layers and unsupervised pre-training for a stack of recurrent NN can be found here. Plus lots of additional material and images related to other refs in the present page.]

[UN3] J.  Schmidhuber, M. C. Mozer, and D. Prelinger. Continuous history compression. In H. Hüning, S. Neuhauser, M. Raus, and W. Ritschel, editors, Proc. of Intl. Workshop on Neural Networks, RWTH Aachen, pages 87-95. Augustinus, 1993.

[UN4] G. E. Hinton, R. R. Salakhutdinov. Reducing the dimensionality of data with neural networks. Science, Vol. 313. no. 5786, pp. 504 - 507, 2006. PDF.

[HB96] S. El Hihi, Y. Bengio. Hierarchical recurrent neural networks for long-term dependencies. NIPS, 1996.

[CW] J. Koutnik, K. Greff, F. Gomez, J. Schmidhuber. A Clockwork RNN. Proc. 31st International Conference on Machine Learning (ICML), p. 1845-1853, Beijing, 2014. Preprint arXiv:1402.3511 [cs.NE].

[FAST] C. v.d. Malsburg. Tech Report 81-2, Abteilung f. Neurobiologie, Max-Planck Institut f. Biophysik und Chemie, Goettingen, 1981.

[FASTb] G. E. Hinton, D. C. Plaut. Using fast weights to deblur old memories. Proc. 9th annual conference of the Cognitive Science Society (pp. 177-186), 1987.

[FAST0] J.  Schmidhuber. Learning to control fast-weight memories: An alternative to recurrent nets. Technical Report FKI-147-91, Institut für Informatik, Technische Universität München, March 1991. PDF.

[FAST1] J. Schmidhuber. Learning to control fast-weight memories: An alternative to recurrent nets. Neural Computation, 4(1):131-139, 1992. PDF. HTML. Pictures (German).

[FAST2] J. Schmidhuber. Reducing the ratio between learning complexity and number of time-varying variables in fully recurrent nets. In Proceedings of the International Conference on Artificial Neural Networks, Amsterdam, pages 460-463. Springer, 1993. PDF.

[FAST3] I. Schlag, J. Schmidhuber. Gated Fast Weights for On-The-Fly Neural Program Generation. Workshop on Meta-Learning, @NIPS 2017, Long Beach, CA, USA.

[FAST3a] I. Schlag, J. Schmidhuber. Learning to Reason with Third Order Tensor Products. Advances in Neural Information Processing Systems (NIPS), Montreal, 2018. Preprint: arXiv:1811.12143. PDF.

[FASTMETA1] J. Schmidhuber. Steps towards `self-referential' learning. Technical Report CU-CS-627-92, Dept. of Comp. Sci., University of Colorado at Boulder, November 1992.

[FASTMETA2] J. Schmidhuber. A self-referential weight matrix. In Proceedings of the International Conference on Artificial Neural Networks, Amsterdam, pages 446-451. Springer, 1993. PDF.

[FASTMETA3] J. Schmidhuber. An introspective network that can learn to run its own weight change algorithm. In Proc. of the Intl. Conf. on Artificial Neural Networks, Brighton, pages 191-195. IEE, 1993.

[FAST4a] J. Ba, G. Hinton, V. Mnih, J. Z. Leibo, C. Ionescu. Using Fast Weights to Attend to the Recent Past. NIPS 2016. PDF.

[FAST5] F. J. Gomez and J. Schmidhuber. Evolving modular fast-weight networks for control. In W. Duch et al. (Eds.): Proc. ICANN'05, LNCS 3697, pp. 383-389, Springer-Verlag Berlin Heidelberg, 2005. PDF. HTML overview.

[KO0] J.  Schmidhuber. Discovering problem solutions with low Kolmogorov complexity and high generalization capability. Technical Report FKI-194-94, Fakultät für Informatik, Technische Universität München, 1994. PDF.

[KO1] J.  Schmidhuber. Discovering solutions with low Kolmogorov complexity and high generalization capability. In A. Prieditis and S. Russell, editors, Machine Learning: Proceedings of the Twelfth International Conference (ICML 1995), pages 488-496. Morgan Kaufmann Publishers, San Francisco, CA, 1995. PDF.

[KO2] J. Schmidhuber. Discovering neural nets with low Kolmogorov complexity and high generalization capability. Neural Networks, 10(5):857-873, 1997. PDF.

[CO1] J. Koutnik, F. Gomez, J. Schmidhuber (2010). Evolving Neural Networks in Compressed Weight Space. Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2010), Portland, 2010. PDF.

[CO2] J. Koutnik, G. Cuccu, J. Schmidhuber, F. Gomez. Evolving Large-Scale Neural Networks for Vision-Based Reinforcement Learning. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), Amsterdam, July 2013. PDF.

[CO3] R. K. Srivastava, J. Schmidhuber, F. Gomez. Generalized Compressed Network Search. Proc. GECCO 2012. PDF.

[DM1] V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wierstra, M. Riedmiller. Playing Atari with Deep Reinforcement Learning. Tech Report, 19 Dec. 2013, arxiv:1312.5602.

[DM2] V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness, M. G. Bellemare, A. Graves, M. Riedmiller, A. K. Fidjeland, G. Ostrovski, S. Petersen, C. Beattie, A. Sadik, I. Antonoglou, H. King, D. Kumaran, D. Wierstra, S. Legg, D. Hassabis. Human-level control through deep reinforcement learning. Nature, vol. 518, p 1529, 26 Feb. 2015. Link.

[DM3] S. Stanford. DeepMind's AI, AlphaStar Showcases Significant Progress Towards AGI. Medium ML Memoirs, 2019. [Alphastar has a "deep LSTM core."]

[OAI1] G. Powell, J. Schneider, J. Tobin, W. Zaremba, A. Petron, M. Chociej, L. Weng, B. McGrew, S. Sidor, A. Ray, P. Welinder, R. Jozefowicz, M. Plappert, J. Pachocki, M. Andrychowicz, B. Baker. Learning Dexterity. OpenAI Blog, 2018.

[OAI1a] OpenAI, M. Andrychowicz, B. Baker, M. Chociej, R. Jozefowicz, B. McGrew, J. Pachocki, A. Petron, M. Plappert, G. Powell, A. Ray, J. Schneider, S. Sidor, J. Tobin, P. Welinder, L. Weng, W. Zaremba. Learning Dexterous In-Hand Manipulation. arxiv:1312.5602 (PDF).

[OAI2] OpenAI et al. (Dec 2019). Dota 2 with Large Scale Deep Reinforcement Learning. Preprint arxiv:1912.06680. [An LSTM composes 84% of the model's total parameter count.]

[PM0] J. Schmidhuber. Learning factorial codes by predictability minimization. TR CU-CS-565-91, Univ. Colorado at Boulder, 1991. PDF. More.

[PM1] J. Schmidhuber. Learning factorial codes by predictability minimization. Neural Computation, 4(6):863-879, 1992. Based on [PM0], 1991. PDF. More.

[PM2] J. Schmidhuber, M. Eldracher, B. Foltin. Semilinear predictability minimzation produces well-known feature detectors. Neural Computation, 8(4):773-786, 1996. PDF. More.

[S59] A. L. Samuel. Some studies in machine learning using the game of checkers. IBM Journal on Research and Development, 3:210-229, 1959.

[H90] W. D. Hillis. Co-evolving parasites improve simulated evolution as an optimization procedure. Physica D: Nonlinear Phenomena, 42(1-3):228-234, 1990.

[GAN0] O. Niemitalo. A method for training artificial neural networks to generate missing data within a variable context. Blog post, Internet Archive, 2010

[GAN1] I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, Y. Bengio. Generative adversarial nets. NIPS 2014, 2672-2680, Dec 2014.

[HOP] J. J. Hopfield. Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences of the USA, vol. 79 no. 8 pp. 2554-2558, 1982.

[GOD] Kurt Gödel. Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für Mathematik und Physik, 38:173-198, 1931.

[PHD] J.  Schmidhuber. Dynamische neuronale Netze und das fundamentale raumzeitliche Lernproblem (Dynamic neural nets and the fundamental spatio-temporal credit assignment problem). Dissertation, Institut für Informatik, Technische Universität München, 1990. PDF. HTML.

[AC90] J.  Schmidhuber. Making the world differentiable: On using fully recurrent self-supervised neural networks for dynamic reinforcement learning and planning in non-stationary environments. Technical Report FKI-126-90, TUM, Feb 1990, revised Nov 1990. PDF

[AC90b] J.  Schmidhuber. A possibility for implementing curiosity and boredom in model-building neural controllers. In J. A. Meyer and S. W. Wilson, editors, Proc. of the International Conference on Simulation of Adaptive Behavior: From Animals to Animats, pages 222-227. MIT Press/Bradford Books, 1991. PDF. HTML.

[AC91] J. Schmidhuber. Adaptive confidence and adaptive curiosity. Technical Report FKI-149-91, Inst. f. Informatik, Tech. Univ. Munich, April 1991. PDF.

[AC91b] J.  Schmidhuber. Curious model-building control systems. In Proc. International Joint Conference on Neural Networks, Singapore, volume 2, pages 1458-1463. IEEE, 1991. PDF.

[AC06] J.  Schmidhuber. Developmental Robotics, Optimal Artificial Curiosity, Creativity, Music, and the Fine Arts. Connection Science, 18(2): 173-187, 2006. PDF.

[AC09] J. Schmidhuber. Art & science as by-products of the search for novel patterns, or data compressible in unknown yet learnable ways. In M. Botta (ed.), Et al. Edizioni, 2009, pp. 98-112. PDF. (More on artificial scientists and artists.)

[AC10] J. Schmidhuber. Formal Theory of Creativity, Fun, and Intrinsic Motivation (1990-2010). IEEE Transactions on Autonomous Mental Development, 2(3):230-247, 2010. IEEE link. PDF.

[AC19] J. Schmidhuber. Unsupervised Minimax: Adversarial Curiosity, Generative Adversarial Networks, and Predictability Minimization. 11 Jun 2019. Preprint arXiv/1906.04493.

[PP] J. Schmidhuber. POWERPLAY: Training an Increasingly General Problem Solver by Continually Searching for the Simplest Still Unsolvable Problem. Frontiers in Cognitive Science, 2013. ArXiv preprint (2011): arXiv:1112.5309 [cs.AI]

[PP1] R. K. Srivastava, B. Steunebrink, J. Schmidhuber. First Experiments with PowerPlay. Neural Networks, 2013. ArXiv preprint (2012): arXiv:1210.8385 [cs.AI].

[PP2] V. Kompella, M. Stollenga, M. Luciw, J. Schmidhuber. Continual curiosity-driven skill acquisition from high-dimensional video inputs for humanoid robots. Artificial Intelligence, 2015.

[PLAN2] J.  Schmidhuber. An on-line algorithm for dynamic reinforcement learning and planning in reactive environments. In Proc. IEEE/INNS International Joint Conference on Neural Networks, San Diego, volume 2, pages 253-258, 1990. Based on [AC90].

[PLAN3] J.  Schmidhuber. Reinforcement learning in Markovian and non-Markovian environments. In D. S. Lippman, J. E. Moody, and D. S. Touretzky, editors, Advances in Neural Information Processing Systems 3, NIPS'3, pages 500-506. San Mateo, CA: Morgan Kaufmann, 1991. PDF. Partially based on [AC90].

[PLAN4] J. Schmidhuber. On Learning to Think: Algorithmic Information Theory for Novel Combinations of Reinforcement Learning Controllers and Recurrent Neural World Models. Report arXiv:1210.0118 [cs.AI], 2015.

[PLAN5] One Big Net For Everything. Preprint arXiv:1802.08864 [cs.AI], Feb 2018.

[PLAN6] D. Ha, J. Schmidhuber. Recurrent World Models Facilitate Policy Evolution. Advances in Neural Information Processing Systems (NIPS), Montreal, 2018. (Talk.) Preprint: arXiv:1809.01999. Github: World Models.

[TD] R. Sutton. Learning to predict by the methods of temporal differences. Machine Learning. 3 (1): 9-44, 1988.

[GVF] R. Sutton, J. Modayil, M. Delp, T. De-gris, P. M. Pilarski, A. White, AD. Precup. Horde: A scalable real-time architecture for learning knowledge from unsupervised sensorimotor interaction. 10th International Conference on Autonomous Agents and Multiagent Systems-Volume 2, pp.761-768, 2011.

[BPTT1] P. J. Werbos. Backpropagation through time: what it does and how to do it. Proceedings of the IEEE 78.10, 1550-1560, 1990.

[BPTT2] R. J. Williams and D. Zipser. Gradient-based learning algorithms for recurrent networks. In: Backpropagation: Theory, architectures, and applications, p 433, 1995.

[PG] R. J. Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learning 8.3-4: 229-256, 1992.

[DPG] D. Silver, G. Lever, N. Heess, T. Degris, D. Wierstra, M. Riedmiller. Deterministic policy gradient algorithms. Proceedings of ICML'31, Beijing, China, 2014. JMLR: W&CP volume 32.

[DDPG] T. P. Lillicrap, J. J. Hunt, A. Pritzel, N. Heess, T. Erez, Y. Tassa, D. Silver, D. Wierstra. Continuous control with deep reinforcement learning. Preprint arXiv:1509.02971, 2015.

[BB1] J.  Schmidhuber. A local learning algorithm for dynamic feedforward and recurrent networks. Technical Report FKI-124-90, Institut für Informatik, Technische Universität München, 1990. PDF.

[BB2] J. Schmidhuber. A local learning algorithm for dynamic feedforward and recurrent networks. Connection Science, 1(4):403-412, 1989. (The Neural Bucket Brigade - figures omitted!). PDF. HTML.

[NAN1] J.  Schmidhuber. Networks adjusting networks. In J. Kindermann and A. Linden, editors, Proceedings of `Distributed Adaptive Neural Information Processing', St.Augustin, 24.-25.5. 1989, pages 197-208. Oldenbourg, 1990. Extended version: TR FKI-125-90 (revised), Institut für Informatik, TUM. PDF.

[NAN2] J.  Schmidhuber. Networks adjusting networks. Technical Report FKI-125-90, Institut für Informatik, Technische Universität München. Revised in November 1990. PDF.

[NAN3] Recurrent networks adjusted by adaptive critics. In Proc. IEEE/INNS International Joint Conference on Neural Networks, Washington, D. C., volume 1, pages 719-722, 1990.

[NAN4] J. Schmidhuber. Additional remarks on G. Lukes' review of Schmidhuber's paper `Recurrent networks adjusted by adaptive critics'. Neural Network Reviews, 4(1):43, 1990.

[NAN5] M. Jaderberg, W. M. Czarnecki, S. Osindero, O. Vinyals, A. Graves, D. Silver, K. Kavukcuoglu. Decoupled Neural Interfaces using Synthetic Gradients. Preprint arXiv:1608.05343, 2016.

[FM] S. Hochreiter and J. Schmidhuber. Flat minimum search finds simple nets. Technical Report FKI-200-94, Fakultät für Informatik, Technische Universität München, December 1994. PDF.

[META1] J. Schmidhuber. Evolutionary principles in self-referential learning, or on learning how to learn: The meta-meta-... hook. Diploma thesis, Tech Univ. Munich, 1987. HTML.

[VAN1] S. Hochreiter. Untersuchungen zu dynamischen neuronalen Netzen. Diploma thesis, TUM, 1991 (advisor J.S.) PDF. [More on the Fundamental Deep Learning Problem.]

[VAN2] Y. Bengio, P. Simard, P. Frasconi. Learning long-term dependencies with gradient descent is difficult. IEEE TNN 5(2), p 157-166, 1994

[VAN3] S. Hochreiter, Y. Bengio, P. Frasconi, J. Schmidhuber. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. In S. C. Kremer and J. F. Kolen, eds., A Field Guide to Dynamical Recurrent Neural Networks. IEEE press, 2001. PDF.

[VAN4] Y. Bengio. Neural net language models. Scholarpedia, 3(1):3881, 2008. Link.

[LSTM0] S. Hochreiter and J. Schmidhuber. Long Short-Term Memory. TR FKI-207-95, TUM, August 1995. PDF.

[LSTM1] S. Hochreiter, J. Schmidhuber. Long Short-Term Memory. Neural Computation, 9(8):1735-1780, 1997. PDF. Based on [LSTM0]. More.

[LSTM2] F. A. Gers, J. Schmidhuber, F. Cummins. Learning to Forget: Continual Prediction with LSTM. Neural Computation, 12(10):2451-2471, 2000. PDF. [The "vanilla LSTM architecture" that everybody is using today, e.g., in Google's Tensorflow.]

[LSTM3] A. Graves, J. Schmidhuber. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Networks, 18:5-6, pp. 602-610, 2005. PDF.

[LSTM4] S. Fernandez, A. Graves, J. Schmidhuber. An application of recurrent neural networks to discriminative keyword spotting. Intl. Conf. on Artificial Neural Networks ICANN'07, 2007. PDF.

[LSTM5] A. Graves, M. Liwicki, S. Fernandez, R. Bertolami, H. Bunke, J. Schmidhuber. A Novel Connectionist System for Improved Unconstrained Handwriting Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 5, 2009. PDF.

[LSTM6] A. Graves, J. Schmidhuber. Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks. NIPS'22, p 545-552, Vancouver, MIT Press, 2009. PDF.

[LSTM7] J. Bayer, D. Wierstra, J. Togelius, J. Schmidhuber. Evolving memory cell structures for sequence learning. Proc. ICANN-09, Cyprus, 2009. PDF.

[LSTM8] A. Graves, A. Mohamed, G. E. Hinton. Speech Recognition with Deep Recurrent Neural Networks. ICASSP 2013, Vancouver, 2013. PDF.

[LSTM9] O. Vinyals, L. Kaiser, T. Koo, S. Petrov, I. Sutskever, G. Hinton. Grammar as a Foreign Language. Preprint arXiv:1412.7449 [cs.CL].

[LSTM10] A. Graves, D. Eck and N. Beringer, J. Schmidhuber. Biologically Plausible Speech Recognition with LSTM Neural Nets. In J. Ijspeert (Ed.), First Intl. Workshop on Biologically Inspired Approaches to Advanced Information Technology, Bio-ADIT 2004, Lausanne, Switzerland, p. 175-184, 2004. PDF.

[LSTM11] N. Beringer and A. Graves and F. Schiel and J. Schmidhuber. Classifying unprompted speech by retraining LSTM Nets. In W. Duch et al. (Eds.): Proc. Intl. Conf. on Artificial Neural Networks ICANN'05, LNCS 3696, pp. 575-581, Springer-Verlag Berlin Heidelberg, 2005.

[LSTM12] D. Wierstra, F. Gomez, J. Schmidhuber. Modeling systems with internal state using Evolino. In Proc. of the 2005 conference on genetic and evolutionary computation (GECCO), Washington, D. C., pp. 1795-1802, ACM Press, New York, NY, USA, 2005. Got a GECCO best paper award.

[LSTM13] F. A. Gers and J. Schmidhuber. LSTM Recurrent Networks Learn Simple Context Free and Context Sensitive Languages. IEEE Transactions on Neural Networks 12(6):1333-1340, 2001. PDF.

[S2S] I. Sutskever, O. Vinyals, Quoc V. Le. Sequence to sequence learning with neural networks. In: Advances in Neural Information Processing Systems (NIPS), 2014, 3104-3112.

[CTC] A. Graves, S. Fernandez, F. Gomez, J. Schmidhuber. Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks. ICML 06, Pittsburgh, 2006. PDF.

[DNC] Hybrid computing using a neural network with dynamic external memory. A. Graves, G. Wayne, M. Reynolds, T. Harley, I. Danihelka, A. Grabska-Barwinska, S. G. Colmenarejo, E. Grefenstette, T. Ramalho, J. Agapiou, A. P. Badia, K. M. Hermann, Y. Zwols, G. Ostrovski, A. Cain, H. King, C. Summerfield, P. Blunsom, K. Kavukcuoglu, D. Hassabis. Nature, 538:7626, p 471, 2016.

[PDA1] G.Z. Sun, H.H. Chen, C.L. Giles, Y.C. Lee, D. Chen. Neural Networks with External Memory Stack that Learn Context - Free Grammars from Examples. Proceedings of the 1990 Conference on Information Science and Systems, Vol.II, pp. 649-653, Princeton University, Princeton, NJ, 1990.

[PDA2] M. Mozer, S. Das. A connectionist symbol manipulator that discovers the structure of context-free languages. Proc. NIPS 1993.

[GSR15] Dramatic improvement of Google's speech recognition through LSTM: Alphr Technology, Jul 2015, or 9to5google, Jul 2015

[NAS] B. Zoph, Q. V. Le. Neural Architecture Search with Reinforcement Learning. Preprint arXiv:1611.01578 (PDF), 2017.

[WU] Y. Wu et al. Google's Neural Machine Translation System: Bridging the Gap between Human and Machine Translation. Preprint arXiv:1609.08144 (PDF), 2016.

[GT16] Google's dramatically improved Google Translate of 2016 is based on LSTM, e.g., WIRED, Sep 2016, or siliconANGLE, Sep 2016

[FB17] By 2017, Facebook used LSTM to handle over 4 billion automatic translations per day (The Verge, August 4, 2017); see also Facebook blog by J.M. Pino, A. Sidorov, N.F. Ayan (August 3, 2017)

[LSTM-RL] B. Bakker, F. Linaker, J. Schmidhuber. Reinforcement Learning in Partially Observable Mobile Robot Domains Using Unsupervised Event Extraction. In Proceedings of the 2002 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2002), Lausanne, 2002. PDF.

[HW1] Srivastava, R. K., Greff, K., Schmidhuber, J. Highway networks. Preprints arXiv:1505.00387 (May 2015) and arXiv:1507.06228 (July 2015). Also at NIPS'2015. The first working very deep feedforward nets with over 100 layers. Let g, t, h, denote non-linear differentiable functions. Each non-input layer of a highway net computes g(x)x + t(x)h(x), where x is the data from the previous layer. (Like LSTM with forget gates [LSTM2] for RNNs.) Resnets [HW2] are a special case of this where g(x)=t(x)=const=1. More.

[HW2] He, K., Zhang, X., Ren, S., Sun, J. Deep residual learning for image recognition. Preprint arXiv:1512.03385 (Dec 2015). Residual nets are a special case of highway nets [HW1], with g(x)=1 (a typical highway net initialization) and t(x)=1. More.

[HW3] K. Greff, R. K. Srivastava, J. Schmidhuber. Highway and Residual Networks learn Unrolled Iterative Estimation. Preprint arxiv:1612.07771 (2016). Also at ICLR 2017.

[THE17] S. Baker (2017). Which countries and universities are leading on AI research? Times Higher Education World University Rankings, 2017. Link.

[JOU17] Jouppi et al. (2017). In-Datacenter Performance Analysis of a Tensor Processing Unit. Preprint arXiv:1704.04760

[CNN1] K. Fukushima: Neural network model for a mechanism of pattern recognition unaffected by shift in position - Neocognitron. Trans. IECE, vol. J62-A, no. 10, pp. 658-665, 1979. [More in Scholarpedia.]

[CNN1a] A. Waibel. Phoneme Recognition Using Time-Delay Neural Networks. Meeting of IEICE, Tokyo, Japan, 1987.

[CNN2] Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, L. D. Jackel: Backpropagation Applied to Handwritten Zip Code Recognition, Neural Computation, 1(4):541-551, 1989. PDF.

[CNN3] Weng, J., Ahuja, N., and Huang, T. S. (1993). Learning recognition and segmentation of 3-D objects from 2-D images. Proc. 4th Intl. Conf. Computer Vision, Berlin, Germany, pp. 121-128.

[CNN4] M. A. Ranzato, Y. LeCun: A Sparse and Locally Shift Invariant Feature Extractor Applied to Document Images. Proc. ICDAR, 2007

[GPUCNN] K. Chellapilla, S. Puri, P. Simard. High performance convolutional neural networks for document processing. International Workshop on Frontiers in Handwriting Recognition, 2006. [Speeding up shallow CNNs on GPU by a factor of 4.]

[GPUCNN1] D. C. Ciresan, U. Meier, J. Masci, L. M. Gambardella, J. Schmidhuber. Flexible, High Performance Convolutional Neural Networks for Image Classification. International Joint Conference on Artificial Intelligence (IJCAI-2011, Barcelona), 2011. PDF. ArXiv preprint. [Speeding up deep CNNs on GPU by a factor of 60. Used to win four important computer vision competitions 2011-2012 before others won any with similar approaches.]

[GPUCNN2] D. C. Ciresan, U. Meier, J. Masci, J. Schmidhuber. A Committee of Neural Networks for Traffic Sign Classification. International Joint Conference on Neural Networks (IJCNN-2011, San Francisco), 2011. PDF. HTML overview. [First superhuman performance in a computer vision contest, with half the error rate of humans, and one third the error rate of the closest competitor. This led to massive interest from industry.]

[GPUCNN3] D. C. Ciresan, U. Meier, J. Schmidhuber. Multi-column Deep Neural Networks for Image Classification. Proc. IEEE Conf. on Computer Vision and Pattern Recognition CVPR 2012, p 3642-3649, July 2012. PDF. Longer TR of Feb 2012: arXiv:1202.2745v1 [cs.CV]. More.

[GPUCNN4] A. Krizhevsky, I. Sutskever, G. E. Hinton. ImageNet Classification with Deep Convolutional Neural Networks. NIPS 25, MIT Press, Dec 2012. PDF.

[GPUCNN5] J. Schmidhuber. History of computer vision contests won by deep CNNs on GPU. March 2017. HTML. [How IDSIA used GPU-based CNNs to win four important computer vision competitions 2011-2012 before others started using similar approaches.]

[GPUCNN6] J. Schmidhuber, D. Ciresan, U. Meier, J. Masci, A. Graves. On Fast Deep Nets for AGI Vision. In Proc. Fourth Conference on Artificial General Intelligence (AGI-11), Google, Mountain View, California, 2011. PDF.

[SCAN] J. Masci, A. Giusti, D. Ciresan, G. Fricout, J. Schmidhuber. A Fast Learning Algorithm for Image Segmentation with Max-Pooling Convolutional Networks. ICIP 2013. Preprint arXiv:1302.1690.

[ST] J. Masci, U. Meier, D. Ciresan, G. Fricout, J. Schmidhuber Steel Defect Classification with Max-Pooling Convolutional Neural Networks. Proc. IJCNN 2012. PDF.

[DIST1] J. Schmidhuber, 1991. See [UN1].

[DIST2] O. Vinyals, J. A. Dean, G. E. Hinton. Distilling the Knowledge in a Neural Network. Preprint arXiv:1503.02531 [stat.ML], 2015.

[MLP1] D. C. Ciresan, U. Meier, L. M. Gambardella, J. Schmidhuber. Deep Big Simple Neural Nets For Handwritten Digit Recognition. Neural Computation 22(12): 3207-3220, 2010. ArXiv Preprint. [Showed that plain backprop for deep standard NNs is sufficient to break benchmark records, without any unsupervised pre-training.]

[BPA] H. J. Kelley. Gradient Theory of Optimal Flight Paths. ARS Journal, Vol. 30, No. 10, pp. 947-954, 1960.

[BPB] A. E. Bryson. A gradient method for optimizing multi-stage allocation processes. Proc. Harvard Univ. Symposium on digital computers and their applications, 1961.

[BPC] S. E. Dreyfus. The numerical solution of variational problems. Journal of Mathematical Analysis and Applications, 5(1): 30-45, 1962.

[BP1] S. Linnainmaa. The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors. Master's Thesis (in Finnish), Univ. Helsinki, 1970. See chapters 6-7 and FORTRAN code on pages 58-60. PDF. See also BIT 16, 146-160, 1976. Link.

[BP2] P. J. Werbos. Applications of advances in nonlinear sensitivity analysis. In R. Drenick, F. Kozin, (eds): System Modeling and Optimization: Proc. IFIP, Springer, 1982. PDF. [Extending thoughts in his 1974 thesis.]

[BP4] J. Schmidhuber. Who invented backpropagation? More in [DL2].

[DEEP1] Ivakhnenko, A. G. and Lapa, V. G. (1965). Cybernetic Predicting Devices. CCM Information Corporation. [First working Deep Learners with many layers, learning internal representations.]

[DEEP2] Ivakhnenko, A. G. (1971). Polynomial theory of complex systems. IEEE Transactions on Systems, Man and Cybernetics, (4):364-378.

[NAT1] J. Schmidhuber. Citation bubble about to burst? Nature, vol. 469, p. 34, 6 January 2011. HTML.

[SA17] J. Schmidhuber. Falling Walls: The Past, Present and Future of Artificial Intelligence. Scientific American, Observations, Nov 2017.

[ALL1] A Computer Scientist's View of Life, the Universe, and Everything. LNCS 201-288, Springer, 1997 (submitted 1996). PDF. More.

[ALL2] Algorithmic theories of everything (2000). ArXiv: quant-ph/ 0011122. See also: International Journal of Foundations of Computer Science 13(4):587-612, 2002: PDF. See also: Proc. COLT 2002: PDF. More.

[ALL3] J. Schmidhuber. The Fastest Way of Computing All Universes. In H. Zenil, ed., A Computable Universe. World Scientific, 2012. PDF of preprint. More.

Edit of May 2020: The present article [MIR] influenced later posts [DEC] [HIN] which contain additional relevant references listed below. It also influenced some of the most popular posts and comments of 2019 at reddit/ml, the largest machine learning forum with back then over 800k subscribers. See, e.g., posts [R2-R8] (although my name is frequently misspelled).

[MIR] J. Schmidhuber (10/4/2019). Deep Learning: Our Miraculous Year 1990-1991. See also arxiv:2005.05744 (May 2020).

[DEC] J. Schmidhuber (02/20/2020). The 2010s: Our Decade of Deep Learning / Outlook on the 2020s.

[HIN] J. Schmidhuber (2020). Critique of Honda Prize for Dr. Hinton.

[R2] Reddit/ML, 2019. J. Schmidhuber really had GANs in 1990.

[R3] Reddit/ML, 2019. NeurIPS 2019 Bengio Schmidhuber Meta-Learning Fiasco.

[R4] Reddit/ML, 2019. Five major deep learning papers by G. Hinton did not cite similar earlier work by J. Schmidhuber.

[R5] Reddit/ML, 2019. The 1997 LSTM paper by Hochreiter & Schmidhuber has become the most cited deep learning research paper of the 20th century.

[R6] Reddit/ML, 2019. DanNet, the CUDA CNN of Dan Ciresan in J. Schmidhuber's team, won 4 image recognition challenges prior to AlexNet.

[R7] Reddit/ML, 2019. J. Schmidhuber on Seppo Linnainmaa, inventor of backpropagation in 1970.

[R8] Reddit/ML, 2019. J. Schmidhuber on Alexey Ivakhnenko, godfather of deep learning 1965.

[R11] Reddit/ML, 2020. Schmidhuber: Critique of Honda Prize for Dr. Hinton

[BW] H. Bourlard, C. J. Wellekens (1989). Links between Markov models and multilayer perceptrons. NIPS 1989, p. 502-510.

[BRI] Bridle, J.S. (1990). Alpha-Nets: A Recurrent "Neural" Network Architecture with a Hidden Markov Model Interpretation, Speech Communication, vol. 9, no. 1, pp. 83-92.

[BOU] H Bourlard, N Morgan (1993). Connectionist speech recognition. Kluwer, 1993.

[HYB12] Hinton, G. E., Deng, L., Yu, D., Dahl, G. E., Mohamed, A., Jaitly, N., Senior, A., Vanhoucke, V., Nguyen, P., Sainath, T. N., and Kingsbury, B. (2012). Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process. Mag., 29(6):82-97.

[AC20] J. Schmidhuber. Generative Adversarial Networks are Special Cases of Artificial Curiosity (1990) and also Closely Related to Predictability Minimization (1991). Neural Networks, Volume 127, p 58-66, 2020. Temporary Open Access. Preprint arXiv/1906.04493.

[MGC] MICCAI 2013 Grand Challenge on Mitosis Detection, organised by M. Veta, M.A. Viergever, J.P.W. Pluim, N. Stathonikos, P. J. van Diest of University Medical Center Utrecht.

[GPUCNN7] D. C. Ciresan, A. Giusti, L. M. Gambardella, J. Schmidhuber. Mitosis Detection in Breast Cancer Histology Images using Deep Neural Networks. MICCAI 2013. PDF.

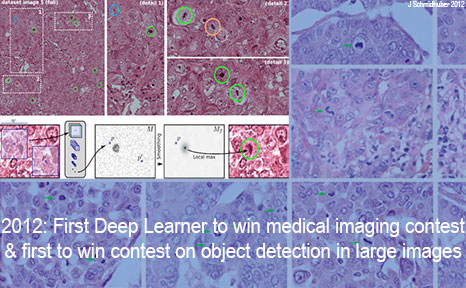
[GPUCNN8] J. Schmidhuber. First deep learner to win a contest on object detection in large images - first deep learner to win a medical imaging contest (2012). HTML. [How IDSIA used GPU-based CNNs to win the ICPR 2012 Contest on Mitosis Detection and the MICCAI 2013 Grand Challenge.]

[LSTM14] S. Fernandez, A. Graves, J. Schmidhuber. Sequence labelling in structured domains with hierarchical recurrent neural networks. In Proc. IJCAI 07, p. 774-779, Hyderabad, India, 2007 (talk). PDF.

[LSTM15] A. Graves, J. Schmidhuber. Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks. Advances in Neural Information Processing Systems 22, NIPS'22, p 545-552, Vancouver, MIT Press, 2009. PDF.

[OAI2a] J. Rodriguez. The Science Behind OpenAI Five that just Produced One of the Greatest Breakthrough in the History of AI. Towards Data Science, 2018. [An LSTM was the core of OpenAI Five.]

[RPG] D. Wierstra, A. Foerster, J. Peters, J. Schmidhuber (2010). Recurrent policy gradients. Logic Journal of the IGPL, 18(5), 620-634.

.