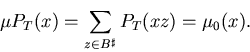Corollary 4.3 and Lemma 4.2
below imply that ![]() and
and ![]() are essentially the same thing: randomly selecting the inputs
of a universal EOM
yields output prefixes whose probabilities are determined
by the universal CEM.
are essentially the same thing: randomly selecting the inputs
of a universal EOM
yields output prefixes whose probabilities are determined
by the universal CEM.
Proof. In the enumeration of EOMs in the proof of Theorem 4.1, let EOM0 be an EOM representing
T applies EOM0 to all ![]() in dovetail fashion,
and simultaneously
simply reads randomly selected input bits forever.
At a given time, let string variable z denote T's input
string read so far.
Starting at the right end of the unit interval [0,1),
as the
in dovetail fashion,
and simultaneously
simply reads randomly selected input bits forever.
At a given time, let string variable z denote T's input
string read so far.
Starting at the right end of the unit interval [0,1),
as the
![]() are being updated by the algorithm of
Theorem 4.1, T
keeps updating a chain of finitely many, variable, disjoint,
consecutive, adjacent, half-open intervals
VI(x)
of size
are being updated by the algorithm of
Theorem 4.1, T
keeps updating a chain of finitely many, variable, disjoint,
consecutive, adjacent, half-open intervals
VI(x)
of size
![]() in alphabetic order on x,
such that VI(y) is to the right of VI(x) if
in alphabetic order on x,
such that VI(y) is to the right of VI(x) if ![]() .
After every variable update and each increase of
z, T replaces its output by the
x of the VI(x) with
.
After every variable update and each increase of
z, T replaces its output by the
x of the VI(x) with
![]() .
Since neither z nor the
.
Since neither z nor the
![]() in the algorithm of Theorem 4.1
can decrease (that is, all interval boundaries can only shift left),
T's output cannot either, and therefore is indeed EOM-computable.
Obviously the following holds:
in the algorithm of Theorem 4.1
can decrease (that is, all interval boundaries can only shift left),
T's output cannot either, and therefore is indeed EOM-computable.
Obviously the following holds: