Robinson und Fallside wiesen als erste darauf hin, daß die Fehlerpropagierungsphase nicht unbedingt notwendig ist [40](siehe auch [39]). Es ist möglich, schon zur Laufzeit der Aktivierungsausbreitungsphase Information aufzusammeln, die bei der Beobachtung von späteren Fehlern sofort zur Berechnung eines Fehlergradienten herangezogen werden kann. Vorteile des Algorithmus sind, daß er eingeschränkt lokal in der Zeit ist, und daß er bei fixer Netzgröße unabhängig von der Länge zu erlernender Sequenzen mit einer fixen Menge an Speicherplatz auskommt. Ein Nachteil ist, daß er nicht einmal eingeschränkt lokal im Raum ist. Der Speicherbedarf wächst schlimmstenfalls mit der dritten Potenz der Anzahl der Knoten.
Weil seine `Lokalität in der Zeit' das Verfahren für unsere Zwecke (siehe Kapitel 6) jedoch sehr interessant macht, und weil die Methode noch nicht gut bekannt ist, werden wir in diesem Abschnitt genauer auf sie eingehen und auch ihre Herleitung aufschreiben. Dabei halten wir uns nicht an Robinsons und Fallsides Originalarbeit, sondern lehnen uns an Williams und Zipsers Beschreibung an [80]. Verwandte Methoden finden sich in [37], [10] und [42].
Die Menge der Eingabeknoten des Netzes sei ![]() .
Die Menge der Knoten des Netzes, die keine Eingabeknoten sind, sei
.
Die Menge der Knoten des Netzes, die keine Eingabeknoten sind, sei ![]() .
.
![]() ist die Aktivation des Knotens
ist die Aktivation des Knotens ![]() aus
aus ![]() zur Zeit
zur Zeit ![]() ,
,
![]() ist die gewünschte Aktivation des Knotens
ist die gewünschte Aktivation des Knotens ![]() zur Zeit
zur Zeit ![]() , falls diese von einem Lehrer definiert worden ist,
, falls diese von einem Lehrer definiert worden ist,
![]() ist das Gewicht der gerichteten Verbindung von Knoten
ist das Gewicht der gerichteten Verbindung von Knoten ![]() zum Knoten
zum Knoten ![]() ,
falls diese Verbindung existiert,
,
falls diese Verbindung existiert,
![]() ist
die sigmoide differenzierbare monoton wachsende Aktivierungsfunktion
des Knotens
ist
die sigmoide differenzierbare monoton wachsende Aktivierungsfunktion
des Knotens ![]() ,
,
![]() ,
,
![]() , und
, und ![]() rangiert im folgenden über
alle Zeitschritte eines Trainingsintervalls.
rangiert im folgenden über
alle Zeitschritte eines Trainingsintervalls.
![]() ist der
zu einem Zeitschritt
ist der
zu einem Zeitschritt ![]() auftretende Fehler, und
auftretende Fehler, und
![]() ist
die zu minimierende Fehlerfunktion.
ist
die zu minimierende Fehlerfunktion.
Der Effekt der Lernregel soll sich wie folgt ausdrücken lassen:
Dabei ist ![]() der Gewichtsvektor des Netzes,
der Gewichtsvektor des Netzes, ![]() eine
positive Lernrate, und
eine
positive Lernrate, und ![]() die von der Lernregel induzierte Gewichtsänderung.
die von der Lernregel induzierte Gewichtsänderung.
Da der Gradient der Summe aller ![]() gleich der Summe der
entsprechenden Gradienten ist, genügt es, für jedes Gewicht
gleich der Summe der
entsprechenden Gradienten ist, genügt es, für jedes Gewicht
![]() den Wert
den Wert
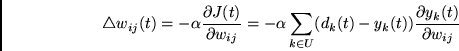
Nun ist für alle Zeitschritte ![]() außer dem letzten
außer dem letzten
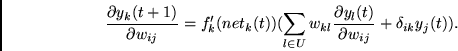
(![]() bezeichnet hier das Kroneckersche Delta und ist 1 für
bezeichnet hier das Kroneckersche Delta und ist 1 für ![]() und
und ![]() sonst.)
sonst.)
Für den ersten Zeitschritt ist die entsprechende Ableitung ![]() .
Also kann man mit
.
Also kann man mit ![]() initialisierte
Variablen
initialisierte
Variablen
![]() und
und
![]() zur inkrementellen Berechnung der
zur inkrementellen Berechnung der
![]() einführen.
Zu jedem Zeitpunkt
einführen.
Zu jedem Zeitpunkt ![]() werden diese Variablen gemäß
werden diese Variablen gemäß
Das im letzten Abschnitt erwähnte Problem mit den vordefinierten Trainingsintervallsgrenzen kann man jetzt umgehen: Statt die Gewichte erst am Ende eines Intervalls zu ändern (wie es mathematisch eigentlich korrekt wäre), ändert man sie zu jedem Zeitschritt. Die Lernrate muß dabei klein genug gewählt werden, um Instabilitäten zu vermeiden. Der Effekt ist, daß sich alle Trainingsintervalle `überlappen'; die Intervallgrenzen verschwimmen und müssen nicht extern definiert werden.