


Next: A.2. HOW TO FLATTEN
Up: APPENDIX - THEORETICAL JUSTIFICATION
Previous: APPENDIX - THEORETICAL JUSTIFICATION
In analogy to
[12] and [1],
we decompose the generalization error into
an ``overfitting'' error and an ``underfitting'' error.
There is no significant
underfitting error (corresponding to Vapnik's empirical risk)
if
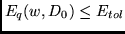 .
Some thought is required, however, to
define the ``overfitting'' error.
We do this in a novel way.
Since we do not know the relation
.
Some thought is required, however, to
define the ``overfitting'' error.
We do this in a novel way.
Since we do not know the relation 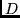 ,
we cannot know
,
we cannot know
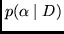 , the ``optimal''
posterior weight distribution
we would obtain by training the net on
, the ``optimal''
posterior weight distribution
we would obtain by training the net on 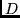 (
(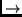 ``sure thing hypothesis'').
But, for theoretical purposes, suppose we did know
``sure thing hypothesis'').
But, for theoretical purposes, suppose we did know
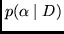 .
Then we could use
.
Then we could use
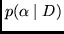 to initialize weights before learning
the training set
to initialize weights before learning
the training set 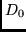 .
Using the Kullback-Leibler distance,
we measure the information (due to noise) conveyed by
.
Using the Kullback-Leibler distance,
we measure the information (due to noise) conveyed by 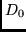 , but
not by
, but
not by 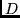 .
In conjunction with
the initialization above,
this provides the conceptual setting for
defining an overfitting error measure.
But, the initialization does not really matter,
because it does not heavily influence the posterior (see [4]).
.
In conjunction with
the initialization above,
this provides the conceptual setting for
defining an overfitting error measure.
But, the initialization does not really matter,
because it does not heavily influence the posterior (see [4]).
The overfitting error is the Kullback-Leibler distance of the posteriors:
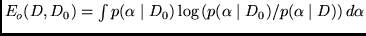 .
.
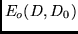 is the expectation of
is the expectation of
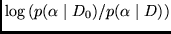 (the expected difference of the minimal
description of
(the expected difference of the minimal
description of
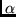 with respect to
with respect to 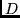 and
and  , after learning
, after learning 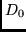 ).
Now we
measure the expected
overfitting error relative to
).
Now we
measure the expected
overfitting error relative to 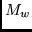 (see section 2)
by computing the expectation of
(see section 2)
by computing the expectation of
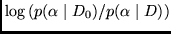 in the range
in the range 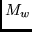 :
:
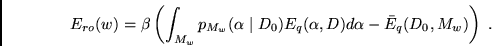 |
(3) |
Here
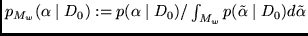 is the posterior of
is the posterior of 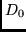 scaled to obtain a distribution within
scaled to obtain a distribution within 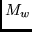 , and
, and
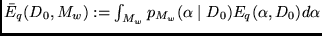 is the mean error
in
is the mean error
in 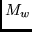 with respect to
with respect to 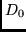 .
.
Clearly, we would like to pick 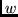 such that
such that
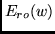 is minimized.
Towards this purpose,
we need two
additional
prior assumptions,
which are actually implicit in most previous
approaches (which make additional stronger assumptions,
see section 1):
(1) ``Closeness assumption'':
Every minimum of
is minimized.
Towards this purpose,
we need two
additional
prior assumptions,
which are actually implicit in most previous
approaches (which make additional stronger assumptions,
see section 1):
(1) ``Closeness assumption'':
Every minimum of 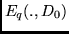 is ``close'' to a maximum
of
is ``close'' to a maximum
of 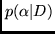 (see formal definition in [4]).
Intuitively, ``closeness'' ensures that
(see formal definition in [4]).
Intuitively, ``closeness'' ensures that
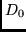 can indeed tell us something about
can indeed tell us something about 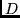 ,
such that training on
,
such that training on 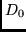 may indeed reduce
the error on
may indeed reduce
the error on 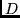 .
(2) ``Flatness assumption'':
The peaks of
.
(2) ``Flatness assumption'':
The peaks of 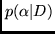 's maxima are not sharp.
This MDL-like assumption
holds if not all weights have to be known
exactly to model
's maxima are not sharp.
This MDL-like assumption
holds if not all weights have to be known
exactly to model 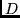 . It
ensures that there are regions with
low error on
. It
ensures that there are regions with
low error on 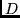 .
.



Next: A.2. HOW TO FLATTEN
Up: APPENDIX - THEORETICAL JUSTIFICATION
Previous: APPENDIX - THEORETICAL JUSTIFICATION
Juergen Schmidhuber
2003-02-25
Back to Financial Forecasting page
![]() .
.
![]() is the expectation of
is the expectation of
![]() (the expected difference of the minimal
description of
(the expected difference of the minimal
description of
![]() with respect to
with respect to ![]() and
and ![]() , after learning
, after learning ![]() ).
Now we
measure the expected
overfitting error relative to
).
Now we
measure the expected
overfitting error relative to ![]() (see section 2)
by computing the expectation of
(see section 2)
by computing the expectation of
![]() in the range
in the range ![]() :
:
![]() such that
such that
![]() is minimized.
Towards this purpose,
we need two
additional
prior assumptions,
which are actually implicit in most previous
approaches (which make additional stronger assumptions,
see section 1):
(1) ``Closeness assumption'':
Every minimum of
is minimized.
Towards this purpose,
we need two
additional
prior assumptions,
which are actually implicit in most previous
approaches (which make additional stronger assumptions,
see section 1):
(1) ``Closeness assumption'':
Every minimum of ![]() is ``close'' to a maximum
of
is ``close'' to a maximum
of ![]() (see formal definition in [4]).
Intuitively, ``closeness'' ensures that
(see formal definition in [4]).
Intuitively, ``closeness'' ensures that
![]() can indeed tell us something about
can indeed tell us something about ![]() ,
such that training on
,
such that training on ![]() may indeed reduce
the error on
may indeed reduce
the error on ![]() .
(2) ``Flatness assumption'':
The peaks of
.
(2) ``Flatness assumption'':
The peaks of ![]() 's maxima are not sharp.
This MDL-like assumption
holds if not all weights have to be known
exactly to model
's maxima are not sharp.
This MDL-like assumption
holds if not all weights have to be known
exactly to model ![]() . It
ensures that there are regions with
low error on
. It
ensures that there are regions with
low error on ![]() .
.