Optimal Universal Search Algorithms

In a sense, searching is less general than reinforcement learning because it does not necessarily involve predictions of unseen data. Still, search is a central aspect of computer science (and any reinforcement learner needs a searcher as a submodule--see Sections 10 and 11). Surprisingly, however, many books on search algorithms do not even mention the following, very simple asymptotically optimal, ``universal'' algorithm for a broad class of search problems.

Define a probability distribution $P$ on a finite or infinite set of programs for a given computer. $P$ represents the searcher's initial bias (e.g., $P$ could be based on program length, or on a probabilistic syntax diagram).

Method LSEARCH: Set current time limit T=1. WHILE problem not solved DO:

Test all programs $q$ such that $t(q)$, the maximal time spent on creating and running and testing $q$, satisfies $t(q) < P(q)~T$. Set $T := 2 T.$

LSEARCH (for Levin Search) may be the algorithm Levin was referring to in his 2 page paper [29] which states that there is an asymptotically optimal universal search method for problems with easily verifiable solutions, that is, solutions whose validity can be quickly tested. Given some problem class, if some unknown optimal program $p$ requires $f(k)$ steps to solve a problem instance of size $k$, then LSEARCH will need at most $O(f(k) / P(p)) = O(f(k))$ steps -- the constant factor $1/P(p)$ may be huge but does not depend on $k$. Compare [31, p. 502-505] and [23] and the fastest way of computing all computable universes in Section 6.

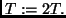
Recently Hutter developed a more complex asymptotically optimal search algorithm for all well-defined problems, not just those with with easily verifiable solutions [23]. HSEARCH cleverly allocates part of the total search time for searching the space of proofs to find provably correct candidate programs with provable upper runtime bounds, and at any given time focuses resources on those programs with the currently best proven time bounds. Unexpectedly, HSEARCH manages to reduce the unknown constant slowdown factor of LSEARCH to a value of $1 + \epsilon$, where $\epsilon$ is an arbitrary positive constant.

Unfortunately, however, the search in proof space introduces an unknown additive problem class-specific constant slowdown, which again may be huge. While additive constants generally are preferrable over multiplicative ones, both types may make universal search methods practically infeasible.

HSEARCH and LSEARCH are nonincremental in the sense that they do not attempt to minimize their constants by exploiting experience collected in previous searches. Our method Adaptive LSEARCH or ALS tries to overcome this [60] -- compare Solomonoff's related ideas [64,65]. Essentially it works as follows: whenever LSEARCH finds a program $q$ that computes a solution for the current problem, $q$'s probability $P(q)$ is substantially increased using a ``learning rate,'' while probabilities of alternative programs decrease appropriately. Subsequent LSEARCHes for new problems then use the adjusted $P$, etc. A nonuniversal variant of this approach was able to solve reinforcement learning (RL) tasks [27] in partially observable environments unsolvable by traditional RL algorithms [74,60].

Each LSEARCH invoked by ALS is optimal with respect to the most recent adjustment of $P$. On the other hand, the modifications of $P$ themselves are not necessarily optimal. Recent work discussed in the next section overcomes this drawback in a principled way.