


Next: Weak Decidability and Convergence
Up: Preliminaries
Previous: Infinite Computations, Convergence, Formal
Much of the traditional theory of computable functions focuses
on halting programs that map subsets of 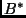 to subsets of
to subsets of 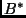 .
The output of a program that does not halt is usually
regarded as undefined, which is occasionally expressed by
notation such as
.
The output of a program that does not halt is usually
regarded as undefined, which is occasionally expressed by
notation such as 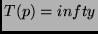 .
In this paper, however, we will not lump together
all the possible outputs of nonhalting programs
onto a single symbol ``undefined.'' Instead we will
consider mappings from subsets of
.
In this paper, however, we will not lump together
all the possible outputs of nonhalting programs
onto a single symbol ``undefined.'' Instead we will
consider mappings from subsets of 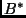 to subsets
of
to subsets
of 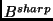 , sometimes from
, sometimes from
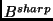 to
to 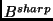 .
.
Definition 2.8 (Encoding
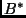
)
Encode
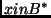
as a self-delimiting input
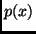
for an appropriate TM, using
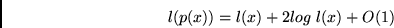 |
(3) |
bits as follows: write
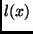
in binary notation,
insert a ``0'' after every ``0'' and a ``1'' after every ``1,''
append ``01'' to indicate the
end of the description of the size of the following string,
then append

.
For instance, 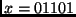 gets encoded as
gets encoded as
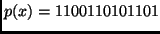 .
.
Definition 2.9 (Recursive Functions)
A function

is
recursive if there is a TM
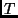
using the encoding
2.8 such that
for all
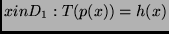
.
Definition 2.10 (Describable Functions)
Let
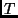
denote a TM using the encoding of Def.
2.8.
A function

is
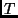
-describable if
for all
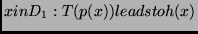
.
Let
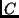
denote a set of TMs using encoding
2.8,
with universal element
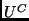
.
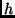
is
C-describable
or
C-computable if it is
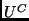 -computable.
-computable.
If the
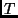
above is universal
among the GTMs with such input encoding
(see Def.
2.3)
then
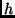
is
describable.
Compare functions in the arithmetic hierarchy [34]
and the concept of  describability, e.g.,
[30, p. 46-47].
describability, e.g.,
[30, p. 46-47].



Next: Weak Decidability and Convergence
Up: Preliminaries
Previous: Infinite Computations, Convergence, Formal
Juergen Schmidhuber
2003-02-13
![]() to subsets of
to subsets of ![]() .
The output of a program that does not halt is usually
regarded as undefined, which is occasionally expressed by
notation such as
.
The output of a program that does not halt is usually
regarded as undefined, which is occasionally expressed by
notation such as ![]() .
In this paper, however, we will not lump together
all the possible outputs of nonhalting programs
onto a single symbol ``undefined.'' Instead we will
consider mappings from subsets of
.
In this paper, however, we will not lump together
all the possible outputs of nonhalting programs
onto a single symbol ``undefined.'' Instead we will
consider mappings from subsets of ![]() to subsets
of
to subsets
of ![]() , sometimes from
, sometimes from
![]() to
to ![]() .
.