



Nächste Seite: `NEURONALE' IMPLEMENTIERUNG
Aufwärts: VORHERSAGBARKEITSMINIMIERUNG
Vorherige Seite: EIN NACHTEIL OBIGER VERFAHREN
Inhalt
Im folgenden stelle ich das von mir bevorzugte Verfahren
zur Implementierung des Prinzips der
Vorhersagbarkeitsminimierung vor. Es leidet nicht unter
dem soeben in Abschnitt 6.3.7 erwähnten Parameterwahlproblem.
Außerdem weist die Methode eine bemerkenswerte Symmetrie
zwischen `sich bekämpfenden' Modulen (vorhersagenden
Prediktoren sowie den Vorhersagen
ausweichenden Repräsentationsmodulen) auf.
Wir definieren
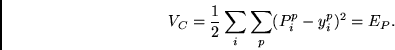 |
(6.8) |
Zur Erinnerung:
Es wird angenommen, daß
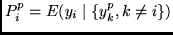 . Man beachte die
formale Äquivalenz von
. Man beachte die
formale Äquivalenz von 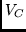 und der Summe der Zielfunktionen
der Prediktoren
und der Summe der Zielfunktionen
der Prediktoren
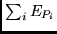 (vergleiche (6.2)).
(vergleiche (6.2)).
Wie in Abschnitt 6.3.6 wird auf den Autoassoziator
verzichtet.
Nun definieren wir die Gesamtzielfunktion 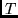 der Repräsentationsknoten
wie folgt um:
der Repräsentationsknoten
wie folgt um:
 |
(6.9) |
Ich will nun die (nicht restlos bewiesene) Vermutung aufstellen, daß
man in (6.9) sogar auf den für das Unabhängigkeitskriterium
zugeschnittenen 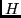 -Term verzichten (also
-Term verzichten (also 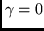 setzen) darf:
setzen) darf:
Vermutung 6.4.1. Existiert für ein gegebenes Ensemble von
Eingabemustern unter den möglichen reellwertigen
Codierungen ein quasi-binärer faktorieller Code,
so ist das Gesamtperformanzmaß
 |
(6.10) |
genau dann maximal, wenn die Repräsentationsmodule
einen derartigen Code gefunden haben.
Es genügt also, wenn alle Repräsentationsmodule versuchen,
dieselbe Zielfunktion zu maximieren, welche von den Prediktoren
minimiert wird.
Für den allgemeinen Fall bleibt diese Vermutung unbewiesen.
Im Appendix zu diesem Kapitel wird sie allerdings
für gewisse Spezialfälle mathematisch gerechtfertigt.
Der Appendix bietet auch etwas
intuitive Rechtfertigung für den allgemeinen Fall.
Schließlich liefert der Appendix eine auf
Peter Dayan und Richard Zemel zurückgehende Argumentation dafür,
daß das Verfahren
aus Abschnitt 6.3.6 und Vorhersagbarkeitsminimerung gemäß
Abschnitt 6.4 für
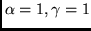 Kraft
im wesentlichen äquivalent sind.
Kraft
im wesentlichen äquivalent sind.
Außerdem haben sich Algorithmen, die ausschließlich auf
der Maximierung von (6.10) beruhen, auch in den später zu
beschreibenden Experimenten bewährt.




Nächste Seite: `NEURONALE' IMPLEMENTIERUNG
Aufwärts: VORHERSAGBARKEITSMINIMIERUNG
Vorherige Seite: EIN NACHTEIL OBIGER VERFAHREN
Inhalt
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite
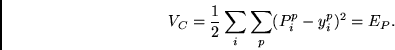
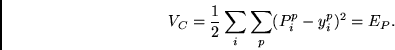
![]() der Repräsentationsknoten
wie folgt um:
der Repräsentationsknoten
wie folgt um:
![]() -Term verzichten (also
-Term verzichten (also ![]() setzen) darf:
setzen) darf:
![]() Kraft
im wesentlichen äquivalent sind.
Kraft
im wesentlichen äquivalent sind.