ERSTE METHODE: `BACK-PROPAGATION THROUGH TIME' (BPTT)

Die Grundidee des folgenden Verfahrens geht auf Minsky und Papert [56] zurück, die darauf hinwiesen, daß die Aktivationsausbreitungsphase eines zyklischen dynamischen Netzes durch die Aktivationsausbreitungsphase eines wesentlich größeren azyklischen statischen Netzes beschrieben werden kann.

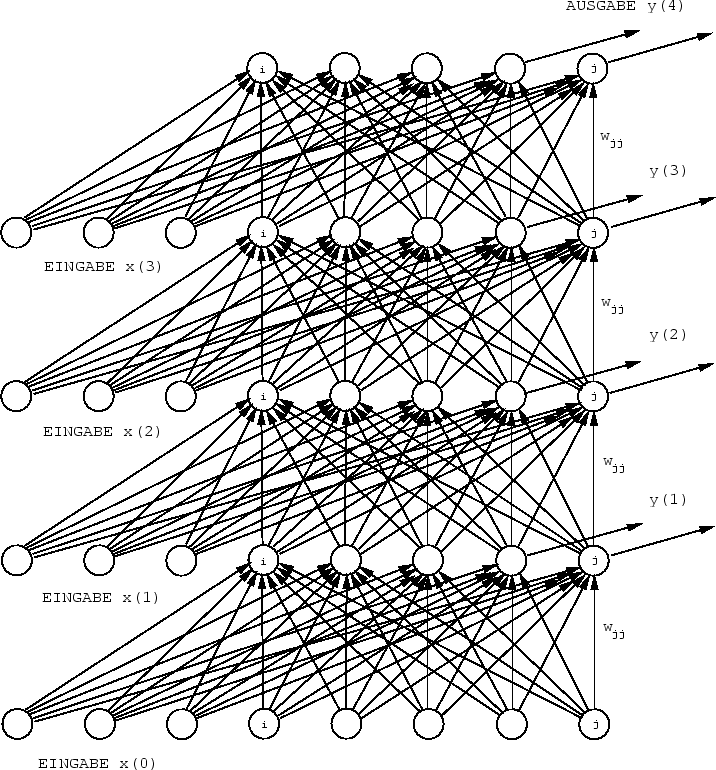
Für jeden Zeitschritt der Aktivationsausbreitungsphase, die ein rekurrentes Netzwerk durchläuft, legt man eine neue Kopie aller Knoten samt ihren gegenwärtigen Aktivationen an. Die Topologie des zu konstruierenden azyklischen Netzes ergibt sich dadurch, daß jede Verbindung des ursprünglichen Netzes in eine `virtuelle' Verbindung transformiert wird, die in dem azyklischen Netz die Kopien der entsprechenden Knoten zu aufeinanderfolgenden Zeitschritten verbindet [85][144] (siehe hierzu Abbildung 2.2).

Abbildung 2.2: Eine 4 Zeitschritte umfassende Aktivationsausbreitungsphase des Netzes aus Abbildung 2.1 im `zeitlich entfalteten' Zustand.

Man kann sich die $w_{ij}(t)$ als Gewichte virtueller Verbindungen zur $t$-ten Lage eines azyklischen Netzes vorstellen. Die Kettenregel liefert uns einen iterativen Algorithmus zur Berechnung von (2.6). Wir schreiben zunächst

$$\delta_i(\tau) = - \frac{\partial E^{total}(0,s) } {\partial net_i(\tau)}.$$

$\delta_i(\tau)$ kann für alle $i \in U, 0 \leq \tau \leq s$ in einem einzigen Pass berechnet werden:

$$\delta_i(\tau) = f_i'(net_i(\tau))e_i(\tau) ~~falls~~\tau = s$$

$$\delta_i(\tau) = f_i'(net_i(\tau))(e_i(\tau) + \sum_{l \in U} w_{li}\delta_l(\tau +1)) ~~falls~~1 \leq \tau < s.$$

Die Berechnungskomplexität dieses Pass (die Anzahl der durchzuführenden Additionen und Multiplikationen) hat die Ordnung $O(sn^2)$.

Nun lassen sich die endgültigen Gewichtsänderungen bestimmen:

$$\triangle w_{ij}(s) = - \alpha \frac{\partial E^{total}(0,s)... ...l w_{ij}} = - \sum_{\tau = 1}^{s} \delta_i(\tau) x_j(\tau -1).$$

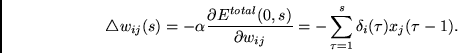
Es ist offenbar nicht nötig, neben den zeitveränderlichen Aktivationen auch die Verbindungen und ihre Gewichte stets von neuem zu kopieren, da es sich ja für jeden Zeitschritt um dieselben Verbindungen handelt. Zweckmäßigerweise führt man für jeden Knoten des zyklischen Netzes einen Stapel ein, auf den die jeweiligen Aktivationen bei sukzessiven Zeitschritten der Aktivationsausbreitungsphase gestapelt werden. Bei der anschließenden Fehlerpropagierungsphase werden die Aktivationen nach dem `last-in-first-out'-Prinzip wieder vom Stapel geholt, um die Fehlersignale zu berechnen.

Komplexität. Egal, wie man den Algorithmus implementiert, in jedem Fall braucht man Speicherplatz unbekannter Größe für den Fall, daß kein Wissen um die Längen der Trainingssequenzen zur Verfügung gestellt wird. Wie wir jedoch später sehen werden, ist BPTT die Methode der Wahl, wenn von vornherein bekannt ist, daß alle Trainingssequenzen weniger als $O(n)$ Zeitschritte umfassen. Die Speicherkomplexität (die Anzahl der Variablen zur Speicherung von Gewichten und zeitlich variierenden Aktivationen) beträgt für einen Durchgang $O(sn + n^2)$. Die Zeitkomplexität (die Anzahl der erforderlichen Multiplikationen und Additionen) pro Durchgang beträgt $O(sn^{2})$. Der Spitzenberechnungsaufwand pro Verbindung und Zeitschritt liegt bei $O(s)$. Das liegt daran, daß im jeweils letzten Zeitschritt eines Trainingsintervalls der gesamte Fehlerpropagierungs- und Gewichtsänderungsprozeß untergebracht werden muß.

`Abgeschnittenes BPTT'. Weiß man von vornherein, daß während der Trainingsphase zwischen Eingabeereignissen und korrelierten Fehlersignalen keine zeitlichen Verzögerungen der Länge $>h$ auftreten, so genügt es, die Fehlersignale zu jedem Zeitpunkt höchstens $h$ Schritte `in die Vergangenheit' zu senden, statt sie (wie bei BPTT vorgeschrieben) bis zum Anfang der Sequenz zurückzupropagieren [149].

Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite