



Nächste Seite: ABSCHLIESSENDE BEMERKUNGEN ZU KAPITEL
Aufwärts: ALGORITHMUS FÜR ÜBERWACHTES LERNEN
Vorherige Seite: PERFORMANZMASS
Inhalt
Mit der Kettenregel berechnen wir Gewichtsinkremente für
die Initialgewichte
 gemäß
gemäß
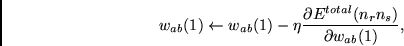 |
(8.12) |
wobei 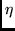 eine konstante positive Lernrate bezeichnet. Damit
erhalten wir einen
exakten gradientenbasierten Algorithmus zur Minimierung von
eine konstante positive Lernrate bezeichnet. Damit
erhalten wir einen
exakten gradientenbasierten Algorithmus zur Minimierung von
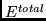 unter der `selbstreferentiellen' durch (8.8) bis (8.11) gegebenen
Dynamik. Um den Schreibaufwand zu reduzieren, seien folgende
(teilweise durch [148] inspirierte)
Kurzschreibweisen eingeführt:
unter der `selbstreferentiellen' durch (8.8) bis (8.11) gegebenen
Dynamik. Um den Schreibaufwand zu reduzieren, seien folgende
(teilweise durch [148] inspirierte)
Kurzschreibweisen eingeführt:
Für alle Knoten 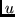 und alle Gewichte
und alle Gewichte 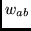 schreiben wir
schreiben wir
 |
(8.13) |
Für alle Verbindungspaare
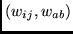 schreiben wir
schreiben wir
 |
(8.14) |
Man beachte zunächst, daß
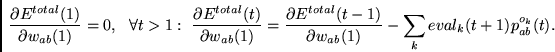 |
(8.15) |
Das verbleibende Problem besteht also in der Berechnung
der
 , welche sich durch inkrementelle
Berechnung aller
, welche sich durch inkrementelle
Berechnung aller
 und
und
 vollziehen läßt, wie wir gleich sehen werden.
vollziehen läßt, wie wir gleich sehen werden.
Für den Zeitpunkt 1 gilt
 |
(8.16) |
Für  erhalten wir die Rekursion
erhalten wir die Rekursion
 |
(8.17) |
 |
(8.18) |
![\begin{displaymath}
w_{ij}(t)~
[~~
g'(\Vert ana(t) - adr(w_{ij})\Vert^2 )
2 \sum_m (ana_m(t) - adr_m(w_{ij})) p_{ab}^{ana_m}(t)
~~]~
~~\}
\end{displaymath}](img915.png) |
(8.19) |
(wobei
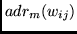 das
das  -te Bit der Adresse von
-te Bit der Adresse von 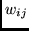 bezeichnet),
bezeichnet),
 |
(8.20) |
wobei
 |
(8.21) |
![\begin{displaymath}
2 \bigtriangleup(t-1)~
g'(\Vert mod(t-1) - adr(w_{ij})\Vert^2 )
\sum_m
[mod_m(t-1) - adr_m(w_{ij})]
p_{ab}^{mod_m}(t-1) .
\end{displaymath}](img923.png) |
(8.22) |
Die 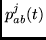 und
und
 lassen sich
gemäß den Gleichungen (8.16)-(8.22) inkrementell zu jedem Zeitschritt
aktualisieren, was bedeutet, daß auch
(8.15) und (8.12) inkrementell berechnet werden können.
Die Speicherkomplexität beträgt unabhängig von
der Sequenzlänge
lassen sich
gemäß den Gleichungen (8.16)-(8.22) inkrementell zu jedem Zeitschritt
aktualisieren, was bedeutet, daß auch
(8.15) und (8.12) inkrementell berechnet werden können.
Die Speicherkomplexität beträgt unabhängig von
der Sequenzlänge
 .
Der Berechnungsaufwand pro Zeitschritt beträgt unabhängig von
der Sequenzlänge
.
Der Berechnungsaufwand pro Zeitschritt beträgt unabhängig von
der Sequenzlänge
 . Dies übertrifft bedauerlicherweise
sogar die Berechnungskomplexität von RTRL (siehe Kapitel 2), welche gleich
. Dies übertrifft bedauerlicherweise
sogar die Berechnungskomplexität von RTRL (siehe Kapitel 2), welche gleich
 ist.
ist.
Ein weiterer Nachteil (neben der hohen Komplexität)
ist die hohe Anzahl lokaler Minima
der ungewöhnlich komplexen Zielfunktion.
Der Zweck dieses letzten Kapitels der Arbeit besteht jedoch nicht in
der Auffindung des effizientesten oder praktikabelsten
gradientenbasierten `selbstreferentiellen' Lernalgorithmus,
sondern in der Demonstration,
daß solche Algorithmen überhaupt theoretisch möglich
sind.
Offenbar gerät der Algorithmus nicht in eine endlose Rekursion.
Er verwendet Gradientenabstieg, um Gewichtsänderungsalgorithmen
zu finden, die zwar nicht notwendigerweise Gradientenabstieg
betreiben (sondern möglicherweise etwas Raffinierteres), aber
dennoch dazu beitragen,
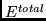 zu minimieren. Damit läßt sich das Gesamtsystem als
eine `selbstreferentielle' Erweiterung der `konventionelleren'
Algorithmen aus Kapitel 2 ansehen.
Beschleunigungsverfahren à la Kapitel 2 sind möglich,
für die Zwecke des vorliegenden Kapitels jedoch nicht von Belang.
zu minimieren. Damit läßt sich das Gesamtsystem als
eine `selbstreferentielle' Erweiterung der `konventionelleren'
Algorithmen aus Kapitel 2 ansehen.
Beschleunigungsverfahren à la Kapitel 2 sind möglich,
für die Zwecke des vorliegenden Kapitels jedoch nicht von Belang.




Nächste Seite: ABSCHLIESSENDE BEMERKUNGEN ZU KAPITEL
Aufwärts: ALGORITHMUS FÜR ÜBERWACHTES LERNEN
Vorherige Seite: PERFORMANZMASS
Inhalt
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite
![]() und alle Gewichte
und alle Gewichte ![]() schreiben wir
schreiben wir
![]() schreiben wir
schreiben wir
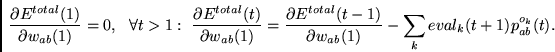
![]() erhalten wir die Rekursion
erhalten wir die Rekursion
![\begin{displaymath}
p^{val}_{ab}(t+1) =
\sum_{i,j}
\frac{\partial} {\partial w_{ab}(1)}
[~ g(\Vert ana(t) - adr(w_{ij})\Vert^2)w_{ij}(t) ~]
=
\end{displaymath}](img913.png)
![\begin{displaymath}
\forall t>1:~~
q^{ij}_{ab}(t) =
\frac{\partial}
{\partial ...
...angleup(\tau)g(\Vert mod(\tau) - adr(w_{ij})\Vert^2) \right] =
\end{displaymath}](img920.png)
![]() und
und
![]() lassen sich
gemäß den Gleichungen (8.16)-(8.22) inkrementell zu jedem Zeitschritt
aktualisieren, was bedeutet, daß auch
(8.15) und (8.12) inkrementell berechnet werden können.
Die Speicherkomplexität beträgt unabhängig von
der Sequenzlänge
lassen sich
gemäß den Gleichungen (8.16)-(8.22) inkrementell zu jedem Zeitschritt
aktualisieren, was bedeutet, daß auch
(8.15) und (8.12) inkrementell berechnet werden können.
Die Speicherkomplexität beträgt unabhängig von
der Sequenzlänge
![]() .
Der Berechnungsaufwand pro Zeitschritt beträgt unabhängig von
der Sequenzlänge
.
Der Berechnungsaufwand pro Zeitschritt beträgt unabhängig von
der Sequenzlänge
![]() . Dies übertrifft bedauerlicherweise
sogar die Berechnungskomplexität von RTRL (siehe Kapitel 2), welche gleich
. Dies übertrifft bedauerlicherweise
sogar die Berechnungskomplexität von RTRL (siehe Kapitel 2), welche gleich
![]() ist.
ist.
![]() zu minimieren. Damit läßt sich das Gesamtsystem als
eine `selbstreferentielle' Erweiterung der `konventionelleren'
Algorithmen aus Kapitel 2 ansehen.
Beschleunigungsverfahren à la Kapitel 2 sind möglich,
für die Zwecke des vorliegenden Kapitels jedoch nicht von Belang.
zu minimieren. Damit läßt sich das Gesamtsystem als
eine `selbstreferentielle' Erweiterung der `konventionelleren'
Algorithmen aus Kapitel 2 ansehen.
Beschleunigungsverfahren à la Kapitel 2 sind möglich,
für die Zwecke des vorliegenden Kapitels jedoch nicht von Belang.