



Nächste Seite: HERLEITUNG DES ALGORITHMUS
Aufwärts: ALGORITHMUS FÜR ÜBERWACHTES LERNEN
Vorherige Seite: ALGORITHMUS FÜR ÜBERWACHTES LERNEN
Inhalt
Wie stets beim überwachten Lernen wollen wir
 minimieren, wobei
minimieren, wobei
Der folgende Algorithmus zur Minimierung von
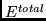 ist teilweise inspiriert durch
die `konventionellen' Lernalgorithmen für rekurrente Netze
aus Kapitel 2 sowie durch
den Algorithmus für das die Gewichte
eines zweiten Netzes
manipulierende nicht
`selbstreferentielle' Netz aus Kapitel 3. Seine Komplexität
übertrifft allerdings die Komplexität der bisher behandelten
Algorithmen.
ist teilweise inspiriert durch
die `konventionellen' Lernalgorithmen für rekurrente Netze
aus Kapitel 2 sowie durch
den Algorithmus für das die Gewichte
eines zweiten Netzes
manipulierende nicht
`selbstreferentielle' Netz aus Kapitel 3. Seine Komplexität
übertrifft allerdings die Komplexität der bisher behandelten
Algorithmen.
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite
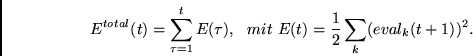
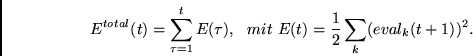
![]() ist teilweise inspiriert durch
die `konventionellen' Lernalgorithmen für rekurrente Netze
aus Kapitel 2 sowie durch
den Algorithmus für das die Gewichte
eines zweiten Netzes
manipulierende nicht
`selbstreferentielle' Netz aus Kapitel 3. Seine Komplexität
übertrifft allerdings die Komplexität der bisher behandelten
Algorithmen.
ist teilweise inspiriert durch
die `konventionellen' Lernalgorithmen für rekurrente Netze
aus Kapitel 2 sowie durch
den Algorithmus für das die Gewichte
eines zweiten Netzes
manipulierende nicht
`selbstreferentielle' Netz aus Kapitel 3. Seine Komplexität
übertrifft allerdings die Komplexität der bisher behandelten
Algorithmen.