



Nächste Seite: GLIEDERUNG DER ARBEIT
Aufwärts: DIE KETTENREGEL
Vorherige Seite: DIE KETTENREGEL
Inhalt
Der wohl bekannteste durch einfache Anwendung der Kettenregel
abgeleitete Lernalgorithmus ist der einführend bereits erwähnte
`back-propagation' Algorithmus (im folgenden stets BP genannt).
BP wurde 1974 erstmals von Werbos im Kontext
der Sozialpsychologie beschrieben [143],
fand jedoch seinerzeit wenig Beachtung
und fiel daraufhin bis etwa Mitte der 80er Jahre
der Vergessenheit anheim.
Das Verfahren wurde verschiedentlich wiederentdeckt
[46][66] und erfreut sich seit Rumelharts, Hintons
und Williams' Veröffentlichung
[85] des Rufs des beliebtesten
Lernverfahrens für KNN.
Die Herleitung des BP-Algorithmus sei
in dieser Einführung aus zwei Gründen vorgeführt:
(1) In den Kapiteln 3, 4, 5, und 6,
werden uns BP-Netze in der Gestalt von Untermodulen umfangreicherer
Netzwerkarchitekturen begegnen.
(2) BP liefert ein besonders einfaches illustratives
Beispiel dafür, daß man mit der Kettenregel im Kontext
maschinellen Lernens etwas Vernünftiges anfangen kann.
Ein BP-Netz ist ein azyklisches Netz. Die Anzahl der Lagen
im Netz sei mit  bezeicnet.
Alle Knoten im Netz seien beliebig durchnumeriert, die Aktivation
des
bezeicnet.
Alle Knoten im Netz seien beliebig durchnumeriert, die Aktivation
des 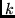 -ten Knotens in Antwort auf
einen an der Eingabelage anliegende Eingabevektor
-ten Knotens in Antwort auf
einen an der Eingabelage anliegende Eingabevektor
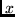 (mit
(mit  -ter Komponente
-ter Komponente  ) heiße
) heiße  ,
wobei
,
wobei 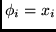 , falls
, falls  Eingabeknoten ist.
In der
Eingabeknoten ist.
In der 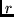 -ten Lage (
-ten Lage ( )
berechnet sich
)
berechnet sich  wie folgt:
wie folgt:
 |
(1.3) |
wobei 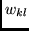 das Gewicht der gerichteten Verbindung vom
Knoten
das Gewicht der gerichteten Verbindung vom
Knoten  zum Knoten
zum Knoten 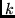 ist, und
ist, und
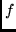 eine reellwertige differenzierbare Aktivierungsfunktion darstellt.
eine reellwertige differenzierbare Aktivierungsfunktion darstellt.
Die Zielfunktion 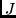 ist in vielen Fällen eine zu minimierende
Fehlerfunktion. Häufig wird der durch
ein einzelnes Muster
ist in vielen Fällen eine zu minimierende
Fehlerfunktion. Häufig wird der durch
ein einzelnes Muster 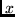 verursachte Fehler
verursachte Fehler 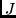 als Summe der
Fehlerquadrate (SFQ)
als Summe der
Fehlerquadrate (SFQ)
gewählt,
wobei 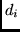 die gewünschte Ausgabe des
die gewünschte Ausgabe des  -ten Ausgabeknotens bezeichnet.
SFQ-Minimierung eignet sich sowohl zur Funktionsapproximation (fast alle
BP-Netze werden gewöhnlich zu diesem Zweck eingesetzt) als auch
zur Modellierung des Erwartungswertes nicht-deterministischer,
teilweise durch die gegenwärtige Eingabe bedingter Ereignisse.
Letztere selten ausgeschöpfte
Möglichkeit wird im 6. Kapitel eine entscheidende Rolle
spielen. Es sei erwähnt, daß
entropiebasierte Zielfunktionen wie z.B. das
Kreuzentropiemaß (e.g. [44], [131])
eine informationstheoretisch begründete Alternative zu SFQ darstellen.
-ten Ausgabeknotens bezeichnet.
SFQ-Minimierung eignet sich sowohl zur Funktionsapproximation (fast alle
BP-Netze werden gewöhnlich zu diesem Zweck eingesetzt) als auch
zur Modellierung des Erwartungswertes nicht-deterministischer,
teilweise durch die gegenwärtige Eingabe bedingter Ereignisse.
Letztere selten ausgeschöpfte
Möglichkeit wird im 6. Kapitel eine entscheidende Rolle
spielen. Es sei erwähnt, daß
entropiebasierte Zielfunktionen wie z.B. das
Kreuzentropiemaß (e.g. [44], [131])
eine informationstheoretisch begründete Alternative zu SFQ darstellen.
Was immer die genaue Form der Zielfunktion 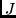 auch sein mag - wir
nehmen an, daß sie in differenzierbarer Form von der Ausgabe des
BP-Netzes abhängt.
Den Bemerkungen aus der Einleitung folgend, interessiert uns
nun für alle Gewichte
auch sein mag - wir
nehmen an, daß sie in differenzierbarer Form von der Ausgabe des
BP-Netzes abhängt.
Den Bemerkungen aus der Einleitung folgend, interessiert uns
nun für alle Gewichte 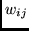 der Gradient
der Gradient
 |
(1.4) |
mit
 |
(1.5) |
Ist  ein Ausgabeknoten, so gewinnt man
den ersten Faktor der rechten Seite von (1.5) sofort
durch partielle Ableitung von
ein Ausgabeknoten, so gewinnt man
den ersten Faktor der rechten Seite von (1.5) sofort
durch partielle Ableitung von 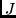 nach
nach 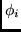 .
Ist
.
Ist  kein Ausgabeknoten und befindet
kein Ausgabeknoten und befindet  sich in Lage
sich in Lage 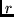 ,
so berechnet sich dieser Faktor mit der Kettenregel (1.2)
zu
,
so berechnet sich dieser Faktor mit der Kettenregel (1.2)
zu
Zur Durchführung eines Iterationsschrittes des
Gradientenabstiegsprozesses wird
jedes Gewicht 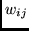 gemäß
gemäß
geändert, wobei  eine positive Konstante, die sogenannte Lernrate,
bezeichnet. Normalerweise ist mehr als ein Eingabemuster
zu berücksichtigen - in diesem Fall hat man
eine positive Konstante, die sogenannte Lernrate,
bezeichnet. Normalerweise ist mehr als ein Eingabemuster
zu berücksichtigen - in diesem Fall hat man
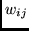 einfach proportional zur
Summe der entsprechenden Gradienten zu ändern (der Gradient einer Summe
ist die Summe der Gradienten).
Die sogenannte
off-line Version von BP spart sich dabei die Ausführung
der Gesamtgewichtsänderung
bis nach der Präsentation aller Trainingsmuster auf.
Im praktischen Einsatz wird findet allerdings häufig
eine sogenannte on-line-Version Verwendung, bei der
Gewichtsänderungen sofort nach der Präsentation jedes
Trainingsmusters durchgeführt werden.
Sowohl on-line als auch
off-line Version führen bei gegen Null gehendem
einfach proportional zur
Summe der entsprechenden Gradienten zu ändern (der Gradient einer Summe
ist die Summe der Gradienten).
Die sogenannte
off-line Version von BP spart sich dabei die Ausführung
der Gesamtgewichtsänderung
bis nach der Präsentation aller Trainingsmuster auf.
Im praktischen Einsatz wird findet allerdings häufig
eine sogenannte on-line-Version Verwendung, bei der
Gewichtsänderungen sofort nach der Präsentation jedes
Trainingsmusters durchgeführt werden.
Sowohl on-line als auch
off-line Version führen bei gegen Null gehendem  einen exakten Gradientenabstieg in
einen exakten Gradientenabstieg in 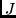 durch.
In Anwendungen (bei Lernraten in der Größenordnung von
0.5) erweist sich die
on-line Version jedoch häufig als günstiger (siehe [26]
für eine theoretische Begründung dieses Sachverhalts).
durch.
In Anwendungen (bei Lernraten in der Größenordnung von
0.5) erweist sich die
on-line Version jedoch häufig als günstiger (siehe [26]
für eine theoretische Begründung dieses Sachverhalts).
Einige der zahlreichen in der Fachliteratur anzutreffenden
BP-Anwendungen führten in gewissen
Domänen zu `state-of-the-art performance' (siehe Einführung).
Wie der Rest dieser Schrift jedoch verdeutlichen wird, gehen die
Anwendungsmöglichkeiten der Kettenregel weit über
BP in azyklischen Netzen hinaus.




Nächste Seite: GLIEDERUNG DER ARBEIT
Aufwärts: DIE KETTENREGEL
Vorherige Seite: DIE KETTENREGEL
Inhalt
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite
![]() bezeicnet.
Alle Knoten im Netz seien beliebig durchnumeriert, die Aktivation
des
bezeicnet.
Alle Knoten im Netz seien beliebig durchnumeriert, die Aktivation
des ![]() -ten Knotens in Antwort auf
einen an der Eingabelage anliegende Eingabevektor
-ten Knotens in Antwort auf
einen an der Eingabelage anliegende Eingabevektor
![]() (mit
(mit ![]() -ter Komponente
-ter Komponente ![]() ) heiße
) heiße ![]() ,
wobei
,
wobei ![]() , falls
, falls ![]() Eingabeknoten ist.
In der
Eingabeknoten ist.
In der ![]() -ten Lage (
-ten Lage (![]() )
berechnet sich
)
berechnet sich ![]() wie folgt:
wie folgt:
![]() ist in vielen Fällen eine zu minimierende
Fehlerfunktion. Häufig wird der durch
ein einzelnes Muster
ist in vielen Fällen eine zu minimierende
Fehlerfunktion. Häufig wird der durch
ein einzelnes Muster ![]() verursachte Fehler
verursachte Fehler ![]() als Summe der
Fehlerquadrate (SFQ)
als Summe der
Fehlerquadrate (SFQ)
![]() auch sein mag - wir
nehmen an, daß sie in differenzierbarer Form von der Ausgabe des
BP-Netzes abhängt.
Den Bemerkungen aus der Einleitung folgend, interessiert uns
nun für alle Gewichte
auch sein mag - wir
nehmen an, daß sie in differenzierbarer Form von der Ausgabe des
BP-Netzes abhängt.
Den Bemerkungen aus der Einleitung folgend, interessiert uns
nun für alle Gewichte ![]() der Gradient
der Gradient