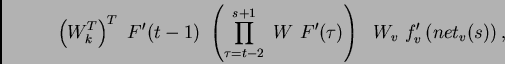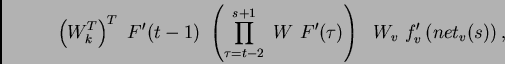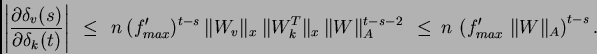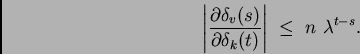Next: Dilemma: Avoiding gradient decay
Up: Exponential error decay
Previous: Intuitive explanation of equation
The following, slightly extended vanishing error analysis
also takes 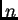 , the number of units, into account.
For
, the number of units, into account.
For 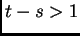 , formula (2) can be rewritten as
, formula (2) can be rewritten as
where the weight matrix 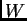 is defined by
is defined by
![$[W]_{ij}:=w_{ij}$](img47.png) ,
, 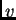 's outgoing weight vector
's outgoing weight vector 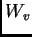 is defined by
is defined by
![$[W_v]_i:=[W]_{iv}=w_{iv}$](img49.png) ,
,
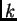 's incoming weight vector
's incoming weight vector 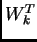 is defined by
is defined by
![$[W^T_k]_i:=[W]_{ki}=w_{ki}$](img51.png) , and
, and
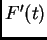 is the diagonal matrix of first order
derivatives defined as:
is the diagonal matrix of first order
derivatives defined as:
![$[F'(t)]_{ij}:= 0$](img53.png) if
if 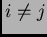 , and
, and
![$[F'(t)]_{ij}:= f'_i(net_i(t))$](img55.png) otherwise.
Here
otherwise.
Here 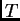 is the transposition operator,
is the transposition operator,
![$[A]_{ij}$](img57.png) is the element in the
is the element in the 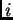 -th column and
-th column and 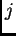 -th row of
matrix
-th row of
matrix 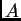 , and
, and ![$[x]_i$](img59.png) is the
is the 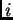 -th component of vector
-th component of vector 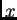 .
Using a matrix norm
.
Using a matrix norm 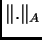 compatible with vector norm
compatible with vector norm 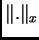 ,
we define
,
we define
For
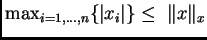 we get
we get
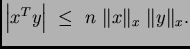 Since
Since
we obtain the following inequality:
This inequality results from
and
where 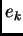 is the unit vector whose components are 0 except
for the
is the unit vector whose components are 0 except
for the 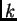 -th component, which is 1.
Note that this is a weak, extreme case upper bound -- it will
be reached only if
all
-th component, which is 1.
Note that this is a weak, extreme case upper bound -- it will
be reached only if
all
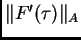 take on maximal values,
and if the contributions of all paths across which error flows back from
unit
take on maximal values,
and if the contributions of all paths across which error flows back from
unit
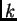 to unit
to unit 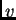 have the same sign.
Large
have the same sign.
Large 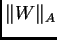 , however, typically result in
small values of
, however, typically result in
small values of
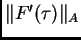 , as confirmed by
experiments (see, e.g., [11]).
For example, with
norms
, as confirmed by
experiments (see, e.g., [11]).
For example, with
norms
and
we have 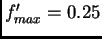 for the logistic sigmoid.
We observe that
if
for the logistic sigmoid.
We observe that
if
then
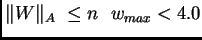 will result in exponential decay; by setting
will result in exponential decay; by setting
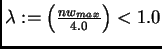 ,
we obtain
,
we obtain
We refer to Hochreiter's thesis [11] for more details.



Next: Dilemma: Avoiding gradient decay
Up: Exponential error decay
Previous: Intuitive explanation of equation
Juergen Schmidhuber
2003-02-19