


Next: EXPERIMENT 2 - recurrent
Up: EXPERIMENTAL RESULTS
Previous: EXPERIMENTAL RESULTS
Task. The first task is taken from
Pearlmutter and Rosenfeld (1991).
The task is to decide whether
the 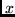 -coordinate of a point in 2-dimensional space
exceeds zero (class 1) or doesn't (class 2).
Noisy training/test examples are generated as follows:
data points are obtained from a Gaussian with
zero mean and stdev 1.0, bounded in the interval
-coordinate of a point in 2-dimensional space
exceeds zero (class 1) or doesn't (class 2).
Noisy training/test examples are generated as follows:
data points are obtained from a Gaussian with
zero mean and stdev 1.0, bounded in the interval ![$[-3.0,3.0]$](img126.png) .
The data points are misclassified
with probability
.
The data points are misclassified
with probability  .
Final input data is obtained by
adding a zero mean Gaussian with stdev 0.15 to the data points.
In a test with 2,000,000 data points,
it was found that the procedure above leads
to 9.27 per cent misclassified data.
No method will misclassify less
than 9.27 per cent, due to the
inherent noise in the data (including the test data).
The training set is based on 200 fixed data points (see
figure 3). The test set
is based on 120,000 data points.
.
Final input data is obtained by
adding a zero mean Gaussian with stdev 0.15 to the data points.
In a test with 2,000,000 data points,
it was found that the procedure above leads
to 9.27 per cent misclassified data.
No method will misclassify less
than 9.27 per cent, due to the
inherent noise in the data (including the test data).
The training set is based on 200 fixed data points (see
figure 3). The test set
is based on 120,000 data points.
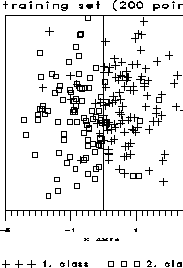
Figure 3:
The 200 input examples of the training set.
Crosses represent data points from class 1. Squares represent data points from
class 0.
 |
Results.
10 conventional backprop (BP) nets were tested
against 10 equally initialized networks trained by
flat minimum search (FMS).
After 1,000 epochs, the weights of our nets essentially stopped changing
(automatic ``early stopping''),
while backprop kept changing weights to learn the outliers in the
data set and overfit.
In the end, our approach left
a single hidden unit  with a maximal weight of
with a maximal weight of  or
or  from the x-axis input. Unlike with backprop,
the other hidden units were effectively pruned away
(outputs near zero).
So was the y-axis input (zero weight to
from the x-axis input. Unlike with backprop,
the other hidden units were effectively pruned away
(outputs near zero).
So was the y-axis input (zero weight to  ).
It can be shown that this corresponds to an ``optimal'' net
with minimal numbers of units and weights.
Table 1 illustrates the superior performance of our approach.
).
It can be shown that this corresponds to an ``optimal'' net
with minimal numbers of units and weights.
Table 1 illustrates the superior performance of our approach.
Table 1:
10 comparisons of conventional backprop (BP)
and flat minimum search (FMS).
The second row (labeled ``MSE'')
shows mean squared error on the test set.
The third row (``dto'')
shows the difference between the
percentage of misclassifications and the optimal
percentage (9.27).
The remaining rows provide the analogous information
for FMS, which clearly outperforms backprop.
| |
Backprop |
FMS |
|
Backprop |
FMS |
| |
MSE |
dto |
MSE |
dto |
|
MSE |
dto |
MSE |
dto |
| 1 |
0.220 |
1.35 |
0.193 |
0.00 |
6 |
0.219 |
1.24 |
0.187 |
0.04 |
| 2 |
0.223 |
1.16 |
0.189 |
0.09 |
7 |
0.215 |
1.14 |
0.187 |
0.07 |
| 3 |
0.222 |
1.37 |
0.186 |
0.13 |
8 |
0.214 |
1.10 |
0.185 |
0.01 |
| 4 |
0.213 |
1.18 |
0.181 |
0.01 |
9 |
0.218 |
1.21 |
0.190 |
0.09 |
| 5 |
0.222 |
1.24 |
0.195 |
0.25 |
10 |
0.214 |
1.21 |
0.188 |
0.07 |
|
Parameters:
Learning rate: 0.1.
Architecture: (2-20-1).
Number of training epochs: 400,000.
With FMS:
 .
.
See section 5.6 for parameters common to all experiments.



Next: EXPERIMENT 2 - recurrent
Up: EXPERIMENTAL RESULTS
Previous: EXPERIMENTAL RESULTS
Juergen Schmidhuber
2003-02-13
Back to Financial Forecasting page


![]() with a maximal weight of
with a maximal weight of ![]() or
or ![]() from the x-axis input. Unlike with backprop,
the other hidden units were effectively pruned away
(outputs near zero).
So was the y-axis input (zero weight to
from the x-axis input. Unlike with backprop,
the other hidden units were effectively pruned away
(outputs near zero).
So was the y-axis input (zero weight to ![]() ).
It can be shown that this corresponds to an ``optimal'' net
with minimal numbers of units and weights.
Table 1 illustrates the superior performance of our approach.
).
It can be shown that this corresponds to an ``optimal'' net
with minimal numbers of units and weights.
Table 1 illustrates the superior performance of our approach.
![]() .
.