It has already been shown that IS by itself
can solve interesting tasks. For instance,
[34] describes
two agents A and B living in a partially
observable
![]() environment with obstacles. They learn to solve a complex task
that could not be solved by various TD(
environment with obstacles. They learn to solve a complex task
that could not be solved by various TD(![]() )
Q-learning variants [15].
The task requires (1) agent A to find and take ``key A'';
(2) agent A go to ``door A'' and open it for agent B;
(3) agent B to enter through ``door A,'' find, and take another ``key B'';
(4) agent B to go to another ``door B'' to open it (to free the way to the goal);
(5) one of the agents to reach the goal.
Both agents share the same design. Each is equipped
with limited ``active'' sight: by executing certain instructions,
it can sense obstacles, its own key,
the corresponding door, or the goal,
within up to 50 unit lengths in front of it.
The agent can also move forward (up to 30 unit lengths),
change its direction, turn relative to its key or its door or the goal.
It can use memory (embodied by its IP)
to disambiguate inputs. Reward is provided only if one of
the agents touches the goal. This agent's reward is 5.0;
the other's is 3.0. In the beginning, the goal is found only every
300,000 basic cycles. Through IS, however,
within 130,000 trials the average trial length
decreases by a factor of 60 -- both agents learn to
cooperate to accelerate reward intake
[34].
)
Q-learning variants [15].
The task requires (1) agent A to find and take ``key A'';
(2) agent A go to ``door A'' and open it for agent B;
(3) agent B to enter through ``door A,'' find, and take another ``key B'';
(4) agent B to go to another ``door B'' to open it (to free the way to the goal);
(5) one of the agents to reach the goal.
Both agents share the same design. Each is equipped
with limited ``active'' sight: by executing certain instructions,
it can sense obstacles, its own key,
the corresponding door, or the goal,
within up to 50 unit lengths in front of it.
The agent can also move forward (up to 30 unit lengths),
change its direction, turn relative to its key or its door or the goal.
It can use memory (embodied by its IP)
to disambiguate inputs. Reward is provided only if one of
the agents touches the goal. This agent's reward is 5.0;
the other's is 3.0. In the beginning, the goal is found only every
300,000 basic cycles. Through IS, however,
within 130,000 trials the average trial length
decreases by a factor of 60 -- both agents learn to
cooperate to accelerate reward intake
[34].
This section's purpose is not to elaborate on how IS can solve difficult tasks. Instead IS is used as a particular vehicle to implement the two-module idea for preliminary attempts at studying ``inquisitive'' explorers. Subsection 4.1 will describe empirically observed system behavior in the absence of external rewards. In Subsection 4.2 there will be additional reward for solving externally posed tasks, to see whether curiosity can indeed be useful.
Experimental details.
There are ![]() instructions (see the appendix)
and
instructions (see the appendix)
and ![]()
![]()
![]() columns per module.
columns per module.
![]() .
Time is measured as follows:
selecting an instruction head,
selecting an argument,
selecting one of the two values required to compute the
next instruction addresses,
pushing or popping a module column
costs one time step.
Other computations do not cost anything. This ensures that
measured time is of the order of total CPU-time.
For instance, selecting an instruction head plus six arguments plus
the next IP address
costs
.
Time is measured as follows:
selecting an instruction head,
selecting an argument,
selecting one of the two values required to compute the
next instruction addresses,
pushing or popping a module column
costs one time step.
Other computations do not cost anything. This ensures that
measured time is of the order of total CPU-time.
For instance, selecting an instruction head plus six arguments plus
the next IP address
costs ![]() time steps.
time steps.
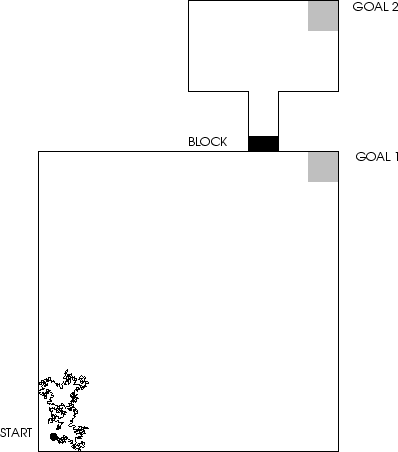
Figure 2 shows a point-like agent's
two-dimensional
environment whose width is 1000 unit lengths.
The large ``room'' in the south is a square. Its
southwest corner has coordinates (0.0, 0.0),
its southeast corner (1000.0, 0.0).
There are infinitely many possible agent states:
the agent's current position is given by a
pair of real numbers. Its
initial coordinates are ![]() ,
its initial direction is 0, its stepsize 12 unit
lengths. Compare appendix
A.3.2.
,
its initial direction is 0, its stepsize 12 unit
lengths. Compare appendix
A.3.2.
 |