


Next: Bibliography
Up: Semantics of Instruction Heads
Previous: Primitive Learning Algorithms
For didactic reasons I wait until the end of this appendix to
introduce a slight change in the basic cycle's instruction
selection procedure (compare Section A.1). In case  addresses an instruction head as opposed to an argument, redefine
addresses an instruction head as opposed to an argument, redefine
If 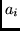 is IncProbRIGHT then
is IncProbRIGHT then  returns the index of
returns the index of
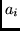 's antagonistic instruction head IncProbLEFT.
Similarly for the other pairs of antagonistic instruction heads:
(DecProbRIGHT, DecProbLEFT), (MoveDistRIGHT,
MoveDistLEFT), (GetRIGHT, GetLEFT),
(EnableSSARIGHT, EnableSSALEFT). This is necessary
because antagonistic instructions require special treatment to
achieve module symmetry through SSAandCopy. For instance,
suppose that LEFT's current advantage depends on supporting
some IncProbRIGHT instruction. An equal RIGHT opponent
should strongly support IncProbLEFT instead.
's antagonistic instruction head IncProbLEFT.
Similarly for the other pairs of antagonistic instruction heads:
(DecProbRIGHT, DecProbLEFT), (MoveDistRIGHT,
MoveDistLEFT), (GetRIGHT, GetLEFT),
(EnableSSARIGHT, EnableSSALEFT). This is necessary
because antagonistic instructions require special treatment to
achieve module symmetry through SSAandCopy. For instance,
suppose that LEFT's current advantage depends on supporting
some IncProbRIGHT instruction. An equal RIGHT opponent
should strongly support IncProbLEFT instead.
Juergen Schmidhuber
2003-03-10
Back to Active Learning - Exploration - Curiosity page