All the module-modifying LIs below save the module columns they change on a stack. The first LEFT-modifying instruction executed after some EnableSSALEFT() instruction will start a new block of LEFT-modifications, to be ended by the next EnableSSALEFT(). Analogously for RIGHT.
IncProbLEFT():
1. Call SSALEFT().
2. If there is not already someentry above the most recent (checkpoint,
(checkpoint)) pair in Stack
, then push the pair
onto Stack
.
3. Set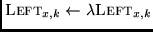
Set
.
Hereis a real-valued constant. In the experiments I arbitrarily use
. Note that step 3. includes renormalization.
IncProbLEFT has no effect though if the corresponding module modifications would lead to at least one LEFT value below MinProb, a small positive real value (I use MinProb).
Comment: IncProbLEFT is an LI that permits LEFT to modify itself (provided RIGHT agrees). IncProbLEFT instructions may be used in conjunction with other instructions to form complex probabilistic learning algorithms (running between subsequent checkpoints).
DecProbLEFT(): like IncProbLEFT, but step 3. is different:
3.;
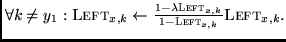
MoveDistLEFT(): like IncProbLEFT, but step 3. is different:
3..
IncProbRIGHT(): analogous to IncProbLEFT.
DecProbRIGHT(): analogous to DecProbLEFT.
MoveDistRIGHT(): analogous to MoveDistLEFT.
IncProbBOTH(): call IncProbLEFT and IncProbRIGHT in random order.
DecProbBOTH(): call DecProbLEFT and DecProbRIGHT in random order.
SSAandCopy(): If
then exit (the value 5 is chosen arbitrarily). Set BlockSSALEFT and BlockSSARIGHT
FALSE. Call SSALEFT() and SSARIGHT() in random order. Test if one of the modules has received more reward per time (since the most recent checkpoint still in its stack) than the other. If so:
Find those columns in the superior module that differ from the corresponding columns in the ``loser.'' (In my implementation this is done efficiently by using a separate stack and a marker array tracing module differences as they occur.) Push the loser's different columns onto the loser's stack (just like with IncProbLEFT and all other LIs). Then copy the winner's different columns onto the loser's.
Comment: the LI SSAandCopy() allows for ending ``unfair'' matches in the case one module consistently outperforms the other. SSAandCopy will make both modules identical, although their stacks will in general be quite different and reflect quite different histories of successful module modifications.