


Next: Algorithm GUESS
Up: The Speed Prior: A
Previous: Speed Prior
Speed Prior-Based Inductive Inference
Given 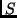 , as we observe an initial segment
, as we observe an initial segment 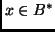 of some string,
which is the most likely continuation?
According to Bayes,
of some string,
which is the most likely continuation?
According to Bayes,
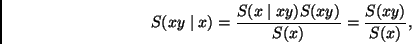 |
(5) |
where
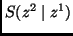 is the measure of
is the measure of 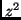 , given
, given 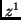 . Having
observed
. Having
observed 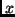 we will predict those
we will predict those 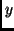 that maximize
that maximize 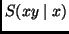 .
Which are those? In what follows, we will confirm the intuition that
for
.
Which are those? In what follows, we will confirm the intuition that
for
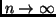 the only probable continuations of
the only probable continuations of 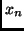 are those with fast programs. The sheer number of ``slowly'' computable
strings cannot balance the speed advantage of ``more quickly'' computable
strings with equal beginnings.
are those with fast programs. The sheer number of ``slowly'' computable
strings cannot balance the speed advantage of ``more quickly'' computable
strings with equal beginnings.
![\begin{definition}[$p \stackrel{< k}{\longrightarrow}_i x$\ etc.]
Write $p \stac...
...$p \stackrel{> k}{\longrightarrow} x$\ (more than $k$\ steps).
\end{definition}](img76.png)
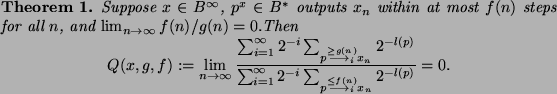
Proof.
Since no program that requires at least 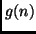 steps for producing
steps for producing
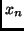 can compute
can compute 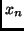 in a PHASE with number
in a PHASE with number 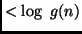 , we have
, we have
Here we have used the Kraft inequality [13]
to obtain a rough upper bound for the enumerator:
when no 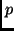 is prefix of another one, then
is prefix of another one, then
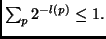 Q.E.D.
Q.E.D.
Hence, if we know a rather fast finite program 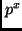 for
for 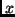 , then Theorem
1 allows for predicting: if we observe some
, then Theorem
1 allows for predicting: if we observe some 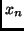 (
(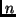 sufficiently large) then it is very unlikely that it was produced by an
sufficiently large) then it is very unlikely that it was produced by an
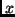 -computing algorithm much slower than
-computing algorithm much slower than 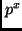 .
.
Among the fastest algorithms for 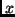 is FAST itself, which is at
least as fast as
is FAST itself, which is at
least as fast as 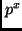 , save for a constant factor. It outputs
, save for a constant factor. It outputs 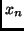 after
after
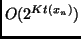 steps.
steps.
Subsections



Next: Algorithm GUESS
Up: The Speed Prior: A
Previous: Speed Prior
Juergen Schmidhuber
2003-02-25
Back to Speed Prior page
![]() , as we observe an initial segment
, as we observe an initial segment ![]() of some string,
which is the most likely continuation?
According to Bayes,
of some string,
which is the most likely continuation?
According to Bayes,
![\begin{definition}[$p \stackrel{< k}{\longrightarrow}_i x$\ etc.]
Write $p \stac...
...$p \stackrel{> k}{\longrightarrow} x$\ (more than $k$\ steps).
\end{definition}](img76.png)
![]() steps for producing
steps for producing
![]() can compute
can compute ![]() in a PHASE with number
in a PHASE with number ![]() , we have
, we have
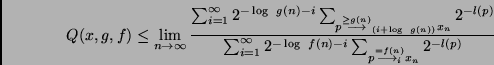
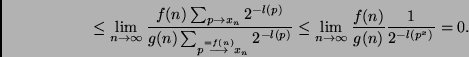
![]() for
for ![]() , then Theorem
1 allows for predicting: if we observe some
, then Theorem
1 allows for predicting: if we observe some ![]() (
(![]() sufficiently large) then it is very unlikely that it was produced by an
sufficiently large) then it is very unlikely that it was produced by an
![]() -computing algorithm much slower than
-computing algorithm much slower than ![]() .
.
![]() is FAST itself, which is at
least as fast as
is FAST itself, which is at
least as fast as ![]() , save for a constant factor. It outputs
, save for a constant factor. It outputs ![]() after
after
![]() steps.
steps.