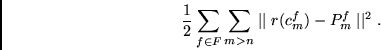With the offline variant of the approach,
![]() 's training phase
is based on a set
's training phase
is based on a set ![]() of training files.
Assume that the alphabet contains
of training files.
Assume that the alphabet contains
![]() possible characters
possible characters
![]() .
The (local) representation of
.
The (local) representation of ![]() is a binary
is a binary ![]() -dimensional
vector
-dimensional
vector ![]() with exactly one non-zero component (at the
with exactly one non-zero component (at the ![]() -th position).
-th position).
![]() has
has ![]() input units and
input units and ![]() output units.
output units.
![]() is called the ``time-window size''.
We insert
is called the ``time-window size''.
We insert ![]() default characters
default characters ![]() at the beginning of each file.
The representation of the
default character,
at the beginning of each file.
The representation of the
default character, ![]() , is the
, is the ![]() -dimensional zero-vector.
The
-dimensional zero-vector.
The ![]() -th character of file
-th character of file ![]() (starting
from the first default character) is called
(starting
from the first default character) is called ![]() .
.
For all ![]() and all possible
and all possible ![]() ,
,
![]() receives as an input
receives as an input