We will now show that there are describable strings that have a short GTM description yet are ``even more random'' than Chaitin's Omegas, in the sense that even on EOMs they do not have any compact descriptions.
Proof. For
![]() and universal
EOM T define
and universal
EOM T define
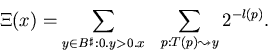 |
(13) |
Algorithm A: Initialize the real-valued variable V by 0, run all possible programs of EOM T dovetail style such that the n-th step of the i-th program is executed in the n+i-th phase; whenever the output of a program prefix q starts with some y satisfying 0.y > 0.x for the first time, set V:= V+ 2-l(q); henceforth ignore continuations of q.V approximates
Suppose we know ![]() .
Once algorithm A above yields
.
Once algorithm A above yields
![]() we know that no programs p with l(p) < n will contribute
any more to V. Choose the shortest z satisfying
0.z = (0.ymin - 0.x)/2,
where ymin is the lexicographically smallest
y previously computed by algorithm A
such that 0.y > 0.x. Then z cannot be among the strings T-describable
with fewer than n bits. Using the Invariance Theorem
(compare Def. 3.3)
we obtain
we know that no programs p with l(p) < n will contribute
any more to V. Choose the shortest z satisfying
0.z = (0.ymin - 0.x)/2,
where ymin is the lexicographically smallest
y previously computed by algorithm A
such that 0.y > 0.x. Then z cannot be among the strings T-describable
with fewer than n bits. Using the Invariance Theorem
(compare Def. 3.3)
we obtain
![]() .
.
While prefixes of ![]() are greatly compressible on EOMs,
z is not.
On the other hand, z is compactly G-describable:
are greatly compressible on EOMs,
z is not.
On the other hand, z is compactly G-describable:
![]() .
For instance, choosing a low-complexity x, we have
.
For instance, choosing a low-complexity x, we have
![]() .
.
![]()
The discussion above reveils a natural complexity hierarchy.
Ignoring additive constants, we have