



Nächste Seite: Gründe für paralleles Lernen
Aufwärts: Begründung des Verfahrens
Vorherige Seite: Begründung des Verfahrens
Inhalt
Wir nehmen zunächst an, daß erst 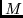 und dann
und dann 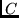 trainiert wird,
und daß alle Gewichte sich nicht während, sondern erst nach
einer Trainingsepisode ändern.
Dann bekommen wir zwar kein `on-line' Verfahren, dafür aber
eine mathematische Rechtfertigung der Methode. Bei der
Implementierung
des praktischen Algorithmus werden wir dann aus
pragmatischen Gründen in verschiedener Hinsicht
wieder vom off-line Ansatz abweichen und
dieses Vorgehen nachträglich durch Experimente rechtfertigen.
trainiert wird,
und daß alle Gewichte sich nicht während, sondern erst nach
einer Trainingsepisode ändern.
Dann bekommen wir zwar kein `on-line' Verfahren, dafür aber
eine mathematische Rechtfertigung der Methode. Bei der
Implementierung
des praktischen Algorithmus werden wir dann aus
pragmatischen Gründen in verschiedener Hinsicht
wieder vom off-line Ansatz abweichen und
dieses Vorgehen nachträglich durch Experimente rechtfertigen.
Für 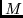 's Lernphase wird in diesem Abschnitt angenommen, daß
die Ausgaben von
's Lernphase wird in diesem Abschnitt angenommen, daß
die Ausgaben von 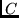 zufällig gewählt werden.
In
zufällig gewählt werden.
In 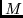 's Ausgabeknoten werden zu jedem Zeitpunkt durch
konventionelle Aktivationsausbreitung (in
's Ausgabeknoten werden zu jedem Zeitpunkt durch
konventionelle Aktivationsausbreitung (in 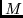 ) die
Voraussagen für
) die
Voraussagen für 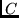 's neue Eingaben (hervorgerufen durch
die externe Rückkopplung oder durch von den Effektoren unabhängige
Umgebungsänderungen) berechnet.
Wir betrachten den Fall vorgegebener Trainingsintervallgrenzen.
's neue Eingaben (hervorgerufen durch
die externe Rückkopplung oder durch von den Effektoren unabhängige
Umgebungsänderungen) berechnet.
Wir betrachten den Fall vorgegebener Trainingsintervallgrenzen.
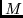 's zu minimierende Fehlerfunktion ist
's zu minimierende Fehlerfunktion ist
wobei
 die Aktivation des
die Aktivation des 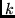 ten vorhersagenden Knotens von
ten vorhersagenden Knotens von 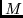 zur
Zeit
zur
Zeit  ist,
ist,
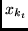 die Aktivation
des entsprechenden vorhergesagten Knotens von
die Aktivation
des entsprechenden vorhergesagten Knotens von 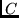 ist und
ist und
 über alle Zeitschritte eines Trainingsintervalls rangiert.
Jedes Gewicht
über alle Zeitschritte eines Trainingsintervalls rangiert.
Jedes Gewicht 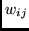 von
von 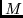 ändert sich dabei proportional zu
ändert sich dabei proportional zu
Ist 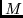 's Lernphase abgeschlossen, so werden seine Gewichte
eingefroren.
's Lernphase abgeschlossen, so werden seine Gewichte
eingefroren. 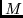 und
und 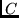 werden zu einem einzigen großen
Netzwerk konkateniert, wobei
werden zu einem einzigen großen
Netzwerk konkateniert, wobei 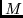 's Ausgabeknoten mit
's Ausgabeknoten mit
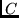 's Eingabeknoten identifiziert werden. Jetzt beginnt
's Eingabeknoten identifiziert werden. Jetzt beginnt 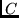 's
Lernphase.
's
Lernphase.
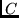 's zu minimierende Fehlerfunktion
's zu minimierende Fehlerfunktion 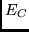 ist
ist
Dabei ist
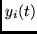 die Aktivation des
die Aktivation des  ten R-Knotens zur Zeit
ten R-Knotens zur Zeit  , und
, und 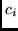 seine
unveränderliche gewünschte Aktivation.
Für die mathematische Begründung wird angenommen,
daß
seine
unveränderliche gewünschte Aktivation.
Für die mathematische Begründung wird angenommen,
daß 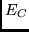 nur noch von
nur noch von 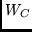 und
und 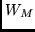 abhängt,
nicht mehr jedoch von der Umgebung.
(Das ist der Systemidentifikationsansatz in seiner allgemeinsten
Form.)
abhängt,
nicht mehr jedoch von der Umgebung.
(Das ist der Systemidentifikationsansatz in seiner allgemeinsten
Form.)
Um Gradientenabstieg zu bekommen, muß ein Gewicht
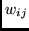 von
von 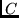 sich proportional zu
sich proportional zu
ändern, und zwar
unter der konstanten Nebenbedingung 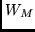 . Abgesehen von einigen
sehr plausiblen, langfristig geradezu notwendigen, im
folgenden ausgeführten
Abweichungen implementiert A2 unter Verwendung des IID-Algorithmus
gerade den Gradientenabstieg
in
. Abgesehen von einigen
sehr plausiblen, langfristig geradezu notwendigen, im
folgenden ausgeführten
Abweichungen implementiert A2 unter Verwendung des IID-Algorithmus
gerade den Gradientenabstieg
in 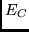 .
.




Nächste Seite: Gründe für paralleles Lernen
Aufwärts: Begründung des Verfahrens
Vorherige Seite: Begründung des Verfahrens
Inhalt
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent neural networks - Subgoal learning - Reinforcement learning and POMDPs - Reinforcement learning economies - Selective attention
Deutsche Heimseite
![]() 's Lernphase wird in diesem Abschnitt angenommen, daß
die Ausgaben von
's Lernphase wird in diesem Abschnitt angenommen, daß
die Ausgaben von ![]() zufällig gewählt werden.
In
zufällig gewählt werden.
In ![]() 's Ausgabeknoten werden zu jedem Zeitpunkt durch
konventionelle Aktivationsausbreitung (in
's Ausgabeknoten werden zu jedem Zeitpunkt durch
konventionelle Aktivationsausbreitung (in ![]() ) die
Voraussagen für
) die
Voraussagen für ![]() 's neue Eingaben (hervorgerufen durch
die externe Rückkopplung oder durch von den Effektoren unabhängige
Umgebungsänderungen) berechnet.
Wir betrachten den Fall vorgegebener Trainingsintervallgrenzen.
's neue Eingaben (hervorgerufen durch
die externe Rückkopplung oder durch von den Effektoren unabhängige
Umgebungsänderungen) berechnet.
Wir betrachten den Fall vorgegebener Trainingsintervallgrenzen.
![]() 's zu minimierende Fehlerfunktion ist
's zu minimierende Fehlerfunktion ist
![]() 's Lernphase abgeschlossen, so werden seine Gewichte
eingefroren.
's Lernphase abgeschlossen, so werden seine Gewichte
eingefroren. ![]() und
und ![]() werden zu einem einzigen großen
Netzwerk konkateniert, wobei
werden zu einem einzigen großen
Netzwerk konkateniert, wobei ![]() 's Ausgabeknoten mit
's Ausgabeknoten mit
![]() 's Eingabeknoten identifiziert werden. Jetzt beginnt
's Eingabeknoten identifiziert werden. Jetzt beginnt ![]() 's
Lernphase.
's
Lernphase.
![]() 's zu minimierende Fehlerfunktion
's zu minimierende Fehlerfunktion ![]() ist
ist
![]() die Aktivation des
die Aktivation des ![]() ten R-Knotens zur Zeit
ten R-Knotens zur Zeit ![]() , und
, und ![]() seine
unveränderliche gewünschte Aktivation.
Für die mathematische Begründung wird angenommen,
daß
seine
unveränderliche gewünschte Aktivation.
Für die mathematische Begründung wird angenommen,
daß ![]() nur noch von
nur noch von ![]() und
und ![]() abhängt,
nicht mehr jedoch von der Umgebung.
(Das ist der Systemidentifikationsansatz in seiner allgemeinsten
Form.)
abhängt,
nicht mehr jedoch von der Umgebung.
(Das ist der Systemidentifikationsansatz in seiner allgemeinsten
Form.)
![]() von
von ![]() sich proportional zu
sich proportional zu