|
1. Recognition of temporally extended patterns in noisy input sequences
2. Recognition of simple regular and context free and context sensitive languages
( Felix Gers, 2000)
3. Recognition of the temporal order of widely separated events in noisy input streams
4. Extraction of information conveyed by the temporal distance between events
5. Stable generation of precisely timed rhythms, smooth and non-smooth periodic trajectories
6. Robust storage of high-precision real numbers across extended time intervals
7. Reinforcement learning in partially observable environments
(Schmidhuber's postdoc
Bram Bakker
,
2001)
8. Metalearning of fast online learning algorithms
(
Sepp Hochreiter
, 2001)
9.
Music improvisation and music composition
(Schmidhuber's former postdoc
Doug Eck
, 2002)
10.
Aspects of speech segmentation and speech recognition (Alex Graves, Nicole
Beringer, 2004).
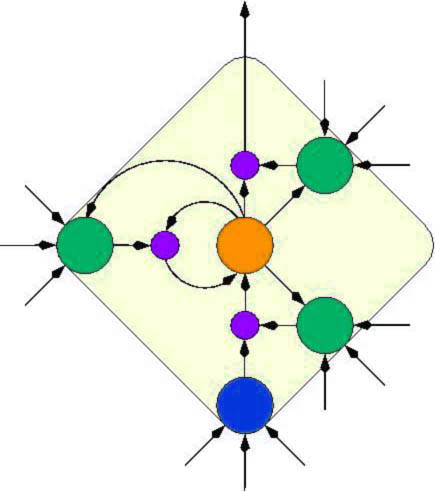
Typical LSTM cell (right):
LSTM networks usually consist of many connected LSTM cells.
Each cell is very simple. At its core there is a linear
unit or neuron (orange).
At any given time it just sums up the inputs that it sees
via its incoming weighted connections.
Its self-recurrent connection has a fixed weight of 1.0
(except when modulated -- via the violet
dot -- through the left green
unit which is not mandatory and which we may ignore for the moment). The 1.0 weight
overcomes THE major problem of previous RNNs by making
sure that training signals "from the future" cannot vanish
as they are being "propagated back in time"
(if this jargon does not make any sense to you,
please consult some RNN papers, e.g., those below).
Suffice it to say here
that the simple linear unit is THE reason why LSTM nets can
learn to discover the importance of events that happened 1000 discrete
time steps ago, while previous RNNs already fail in case of time lags exceeding
as few as 10 steps!
The linear unit is typically surrounded by a cloud of
nonlinear adaptive units which are responsible for learning the nonlinear
aspects of sequence processing. Here we see an input unit (blue)
and three (green) multiplicative gate units (small violet dots
represent multiplications). The gates essentially
learn to protect the central linear unit from irrelevant
input events and error signals.
The LSTM learning algorithm is very efficient --
not more than O(1)
computations
per time step and weight!
Some recent publications on LSTM RNNs:
14.
A. Graves, D. Eck and N. Beringer, J. Schmidhuber.
Isolated Digit Recognition with LSTM Recurrent Networks.
First Intl. Workshop on Biologically
Inspired Approaches to Advanced Information Technology,
2004, in press.
13.
A. Graves, N. Beringer, J. Schmidhuber.
A Comparison Between Spiking and Differentiable Recurrent
Neural Networks on Spoken Digit Recognition.
In Proc. 23rd International Conference on modelling, identification,
and control (IASTED), 2004, in press.
12.
B. Bakker and J. Schmidhuber.
Hierarchical Reinforcement
Learning Based on Subgoal Discovery and Subpolicy Specialization
(PDF).
In F. Groen, N. Amato, A. Bonarini, E. Yoshida, and B. Kröse (Eds.),
Proceedings of the 8-th Conference on Intelligent Autonomous Systems,
IAS-8, Amsterdam, The Netherlands, p. 438-445, 2004.
11.
D. Eck, A. Graves, J. Schmidhuber.
A New Approach to Continuous Speech Recognition Using
LSTM Recurrent Neural Networks.
TR IDSIA-14-03, 2003.
10. J. A. Perez-Ortiz, F. A. Gers, D. Eck, J. Schmidhuber.
Kalman filters improve LSTM network performance in
problems unsolvable by traditional recurrent nets.
Neural Networks 16(2):241-250, 2003.
PDF.
9.
F. Gers, N. Schraudolph, J. Schmidhuber.
Learning precise timing with
LSTM recurrent networks.
Journal of Machine Learning Research 3:115-143, 2002.
PDF.
8.
J. Schmidhuber, F. Gers, D. Eck.
J. Schmidhuber, F. Gers, D. Eck.
Learning nonregular languages:
A comparison of simple recurrent networks and LSTM.
Neural Computation, 14(9):2039-2041, 2002.
PDF.
7.
B. Bakker.
Reinforcement Learning with Long Short-Term Memory.
Advances in Neural Information Processing
Systems 13 (NIPS'13), 2002.
(On J. Schmidhuber's CSEM grant 2002.)
6.
D. Eck and J. Schmidhuber.
Learning The Long-Term Structure of the Blues.
In J. Dorronsoro, ed.,
Proceedings of Int. Conf. on Artificial Neural Networks
ICANN'02, Madrid, pages 284-289, Springer, Berlin, 2002.
PDF.
5.
F. A. Gers and J. Schmidhuber.
LSTM Recurrent Networks Learn Simple Context Free and
Context Sensitive Languages.
IEEE Transactions on Neural Networks 12(6):1333-1340, 2001.
PDF.
4.
F. A. Gers and J. Schmidhuber and F. Cummins.
Learning to Forget: Continual Prediction with LSTM.
Neural Computation, 12(10):2451--2471, 2000.
PDF.
3.
S. Hochreiter and J. Schmidhuber.
Long Short-Term Memory.
Neural Computation, 9(8):1735-1780, 1997.
PDF .
2.
S. Hochreiter and J. Schmidhuber.
LSTM can solve hard long time lag problems.
In M. C. Mozer, M. I. Jordan, T. Petsche, eds.,
Advances in Neural Information Processing Systems 9, NIPS'9,
pages 473-479, MIT Press, Cambridge MA, 1997.
PDF .
HTML.
1.
S. Hochreiter and J. Schmidhuber.
Bridging long time lags by weight guessing and "Long Short-Term
Memory".
In F. L. Silva, J. C. Principe, L. B. Almeida, eds.,
Frontiers in Artificial Intelligence and Applications, Volume 37,
pages 65-72, IOS Press, Amsterdam, Netherlands, 1996.
Please also find numerous additional publications on LSTM in the
home pages of
Juergen Schmidhuber,
Doug Eck,
and
Felix Gers.
Felix's home page also has pointers to LSTM source code.
Additional RNN publications (more
here):
13.
J. Schmidhuber and S. Hochreiter.
Guessing can outperform many long time lag algorithms.
Technical Note IDSIA-19-96, IDSIA, May 1996.
See also NIPS'96 HTML.
12.
J. Schmidhuber.
A self-referential weight matrix.
In Proceedings of the International Conference on Artificial
Neural Networks, Amsterdam, pages 446-451. Springer, 1993.
PDF .
HTML.
11.
J. Schmidhuber.
Reducing the ratio between learning complexity and number of
time-varying variables in fully recurrent nets.
In Proceedings of the International Conference on Artificial
Neural Networks, Amsterdam, pages 460-463. Springer, 1993.
PDF.
HTML.
10.
J. Schmidhuber.
Netzwerkarchitekturen, Zielfunktionen und Kettenregel.
(Net architectures, objective functions, and chain rule.)
Habilitation (postdoctoral thesis - qualification for a
tenure professorship),
Institut für Informatik, Technische Universität
München, 1993 (496 K).
PDF .
HTML.
9.
J. Schmidhuber.
Learning complex,
extended sequences using the principle of history compression.
Neural Computation, 4(2):234-242, 1992 (41 K).
PDF.
HTML.
8.
J. Schmidhuber.
Learning unambiguous reduced sequence descriptions.
In J. E. Moody, S. J. Hanson, and R. P. Lippman, editors,
Advances in Neural Information Processing Systems 4, NIPS'4, pages 291-298. San
Mateo, CA: Morgan Kaufmann, 1992.
PDF .
HTML.
7.
J. Schmidhuber.
A fixed size
storage O(n^3) time complexity learning algorithm for fully recurrent
continually running networks.
Neural Computation, 4(2):243-248, 1992 (33 K).
PDF.
HTML.
6.
J. Schmidhuber.
Learning to
control fast-weight memories: An alternative to recurrent nets.
Neural Computation, 4(1):131-139, 1992 (39 K).
PDF.
HTML.
Pictures (German).
5.
J. Schmidhuber.
Learning temporary variable binding with dynamic links.
In Proc. International Joint Conference on Neural Networks,
Singapore, volume 3, pages 2075-2079. IEEE, 1991.
4.
J. Schmidhuber.
An on-line algorithm for dynamic reinforcement learning and planning
in reactive environments.
In Proc. IEEE/INNS International Joint Conference on Neural
Networks, San Diego, volume 2, pages 253-258, 1990.
3.
J. Schmidhuber.
Learning algorithms for networks with internal and external feedback.
In D. S. Touretzky, J. L. Elman, T. J. Sejnowski,
and G. E. Hinton,
editors, Proc. of the 1990 Connectionist Models Summer School, pages
52-61. San Mateo, CA: Morgan Kaufmann, 1990.
2.
J. Schmidhuber.
Dynamische neuronale Netze und das fundamentale raumzeitliche
Lernproblem. (341 K),
(Dynamic neural nets and the fundamental spatio-temporal
credit assignment problem.) Dissertation,
Institut für Informatik, Technische
Universität München, 1990.
PDF .
HTML.
1.
J. Schmidhuber.
A local learning algorithm for dynamic feedforward and
recurrent networks.
Connection Science, 1(4):403-412, 1989.
(The Neural Bucket Brigade - figures omitted!).
PDF.
HTML.
| 
