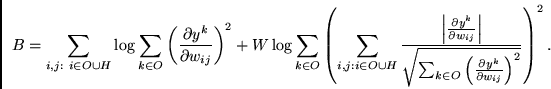FMS is a general gradient-based method for finding low-complexity networks with high generalization capability. FMS finds a large region in weight space such that each weight vector from that region has similar small error. Such regions are called ``flat minima''. In MDL terminology, few bits of information are required to pick a weight vector in a ``flat'' minimum (corresponding to a low-complexity network) -- the weights may be given with low precision. FMS automatically prunes weights and units, and reduces output sensitivity with respect to remaining weights and units. Previous FMS applications focused on supervised learning [13,14].
Notation.
Let ![]() denote
index sets for output, hidden, and input units, respectively.
For
denote
index sets for output, hidden, and input units, respectively.
For
![]() , the activation
, the activation ![]() of unit
of unit ![]() is
is
![]() , where
, where
![]() is the net input of unit
is the net input of unit ![]() (
(![]() for
for ![]() and
and ![]() for
for ![]() ),
),
![]() denotes the
weight on the connection from unit
denotes the
weight on the connection from unit ![]() to unit
to unit ![]() ,
,
![]() denotes the activation function,
and for
denotes the activation function,
and for ![]() ,
, ![]() denotes the
denotes the ![]() -th
component of an input vector.
-th
component of an input vector.
![]() is the number of weights.
is the number of weights.
Algorithm.
FMS' objective function ![]() features an unconventional error term:
features an unconventional error term: