Unbeknownst to many machine learning researchers, there exists a search algorithm with amazing theoretical properties: for a broad class of search problems, Levin search (LS) [#!Levin:73!#,#!Levin:84!#] has the optimal order of computational complexity. See [#!LiVitanyi:93!#] for an overview. See (Schmidhuber 1995, 1997a) for recent implementations/applications.
Basic concepts. LS requires a set of ![]() primitive,
prewired instructions
primitive,
prewired instructions
![]() that can be composed to
form arbitrary sequential programs. Essentially, LS generates and
tests solution candidates
that can be composed to
form arbitrary sequential programs. Essentially, LS generates and
tests solution candidates ![]() (program outputs represented as strings
over a finite alphabet) in order of their Levin complexities
(program outputs represented as strings
over a finite alphabet) in order of their Levin complexities
![]() , where
, where ![]() stands for a program that
computes
stands for a program that
computes ![]() in
in ![]() time steps, and
time steps, and ![]() is the probability of
guessing
is the probability of
guessing ![]() according to a fixed Solomonoff-Levin distribution
[#!LiVitanyi:93!#] on the set of possible programs (in section 3.2,
however, we will make the distribution variable).
according to a fixed Solomonoff-Levin distribution
[#!LiVitanyi:93!#] on the set of possible programs (in section 3.2,
however, we will make the distribution variable).
Optimality. Given primitives representing a
universal programming language, for a broad class of problems
LS can be shown to be optimal with respect to total expected search
time, leaving aside a constant factor independent of the problem size
[#!Levin:73!#,#!Levin:84!#,#!LiVitanyi:93!#]. More formally: a problem is a
symbol string that conveys all information about another symbol string
called its solution, where the solution can be extracted by some (search)
algorithm, given the problem. Suppose there is an algorithm that solves
certain time-limited optimization problems
or inversion problems in ![]() steps, where
steps, where ![]() is a total recursive
function and
is a total recursive
function and ![]() is a positive
integer representing problem size. Then universal LS will solve the
same problems in at most
is a positive
integer representing problem size. Then universal LS will solve the
same problems in at most ![]() steps (although a large constant
may be buried in the
steps (although a large constant
may be buried in the ![]() notation). Despite this strong result, until
recently LS has not received much attention except in purely theoretical
studies -- see, e.g., [#!Watanabe:92!#].
notation). Despite this strong result, until
recently LS has not received much attention except in purely theoretical
studies -- see, e.g., [#!Watanabe:92!#].
Of course, LS and any other algorithm will fail to quickly solve problems whose solutions all have high algorithmic complexity. Unfortunately, almost all possible problems are of this kind [#!Kolmogorov:65!#,#!Chaitin:69!#,#!Solomonoff:64!#]. In fact, the realm of practical computer science is limited to solving the comparatively few tasks with low-complexity solutions. Fortunately such tasks are rather common in our regular universe.
Practical implementation. In our practical LS version there is an
upper bound ![]() on program length (due to obvious storage limitations).
on program length (due to obvious storage limitations).
![]() denotes the address of the
denotes the address of the ![]() -th instruction. Each program
is generated incrementally: first we select an instruction for
-th instruction. Each program
is generated incrementally: first we select an instruction for ![]() ,
then for
,
then for ![]() , etc.
, etc. ![]() is given by a matrix
is given by a matrix ![]() , where
, where ![]() (
(
![]() ,
,
![]() ) denotes the probability
of selecting
) denotes the probability
of selecting ![]() as the instruction at address
as the instruction at address ![]() , given that the
first
, given that the
first ![]() instructions have already been selected. The probability
of a program is the product of the probabilities of its constituents.
instructions have already been selected. The probability
of a program is the product of the probabilities of its constituents.
LS' arguments are ![]() and the representation of a problem denoted by
and the representation of a problem denoted by
![]() . LS' output is a program that computes a solution to the problem if it
found any. In this section, all
. LS' output is a program that computes a solution to the problem if it
found any. In this section, all
![]() will remain
fixed. LS is implemented as a sequence of longer and longer phases:
will remain
fixed. LS is implemented as a sequence of longer and longer phases:
Levin search(problem ![]() , probability matrix
, probability matrix ![]() )
)
(1) Set, the number of the current phase, equal to 1. In what follows, let
denote the set of not yet executed programs
satisfying
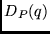
.
(2) Repeat
(2.1) Whileand no solution found do: Generate a program
, and run
until it either halts or until it used up
steps. If
computed a solution for
, return
and exit.
(2.2) Set:= 2

until solution found or

.
Return empty program.
Here ![]() and
and ![]() are prespecified
constants. The procedure above is essentially the same (has the same
order of complexity) as the one described in the second paragraph of
this section -- see, e.g., [#!Solomonoff:86!#,#!LiVitanyi:93!#].
are prespecified
constants. The procedure above is essentially the same (has the same
order of complexity) as the one described in the second paragraph of
this section -- see, e.g., [#!Solomonoff:86!#,#!LiVitanyi:93!#].