Definition 4.17 (TM-Induced Semimeasures
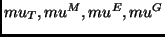
)
Given some TM
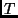
,
for
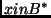
define
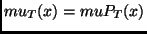
.
Again we deviate a bit from Levin's
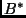
-oriented path
[
45] (survey: [
30, p. 245 ff, p. 272 ff])
and extend
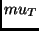
to
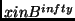
, where we define
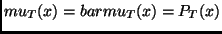
.
If
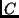
denotes a set of TMs with universal element
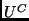
, then we write
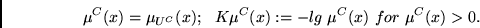 |
(31) |
Corollary 4.2
For
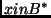
,
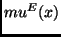
is a CEM and approximable as the difference of two c.e. values:
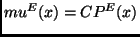
for

without any 0-bit, otherwise
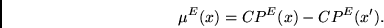 |
(33) |