


Next: EOMs dominate MTMs
Up: Complexity of Constructive Descriptions
Previous: Generalized Kolmogorov Complexity for
Expressiveness of EOMs and GTMs
Since GTMs may occasionally rewrite parts of their output,
they are computationally more expressive than MTMs in the sense
that they permit much more compact descriptions of certain
objects -- compare also [7].
For instance,
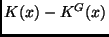 is unbounded, as will be shown next.
This will later have
consequences for predictions, given certain observations.
is unbounded, as will be shown next.
This will later have
consequences for predictions, given certain observations.
Theorem 3.2
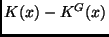
is unbounded.
Proof.
Define
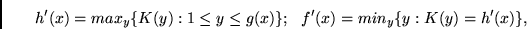 |
(8) |
where 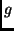 is recursive.
Then
is recursive.
Then
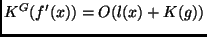 (where
(where  is the size of the minimal
halting description of function
is the size of the minimal
halting description of function 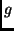 ), but
), but
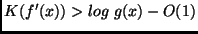 for
sufficiently large
for
sufficiently large  --
compare the proof of Theorem 3.1.
Therefore
--
compare the proof of Theorem 3.1.
Therefore
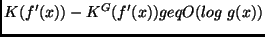 for infinitely many
for infinitely many
 and quickly growing
and quickly growing 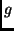 with low complexity.
with low complexity.
Subsections
Juergen Schmidhuber
2003-02-13
![]() is unbounded, as will be shown next.
This will later have
consequences for predictions, given certain observations.
is unbounded, as will be shown next.
This will later have
consequences for predictions, given certain observations.