Basic concepts.
LS requires a set of ![]() primitive, prewired instructions
primitive, prewired instructions ![]() that can be composed to form arbitrary sequential programs.
Essentially, LS generates and tests
solution candidates
that can be composed to form arbitrary sequential programs.
Essentially, LS generates and tests
solution candidates ![]() (program outputs represented
as strings over a finite alphabet)
in order of their Levin complexities
(program outputs represented
as strings over a finite alphabet)
in order of their Levin complexities
![]() ,
where
,
where ![]() stands for a program that computes
stands for a program that computes ![]() in
in ![]() time
steps, and
time
steps, and ![]() is the probability of guessing
is the probability of guessing ![]() according to
a fixed Solomonoff-Levin distribution
[Li and Vitányi, 1993]
on the set of possible programs
(in section 3, however, we will make the distribution variable).
according to
a fixed Solomonoff-Levin distribution
[Li and Vitányi, 1993]
on the set of possible programs
(in section 3, however, we will make the distribution variable).
Optimality. Amazingly, given primitives representing a universal programming language, for a broad class of problems, including all inversion problems and time-limited optimization problems, LS can be shown to be optimal with respect to total expected search time, leaving aside a constant factor independent of the problem size [Levin, 1973,Levin, 1984,Li and Vitányi, 1993]. Still, until recently LS has not received much attention except in purely theoretical studies -- see, e.g., [Watanabe, 1992].
Practical implementation.
In our practical LS version,
there is an upper bound ![]() on program length
(due to obvious storage limitations).
on program length
(due to obvious storage limitations).
![]() denotes the address of the
denotes the address of the ![]() -th instruction.
Each program is generated incrementally: first we
select an instruction for
-th instruction.
Each program is generated incrementally: first we
select an instruction for ![]() , then for
, then for ![]() , etc.
, etc.
![]() is given by a matrix
is given by a matrix ![]() , where
, where
![]() (
(
![]() ,
,
![]() )
denotes the probability of selecting
)
denotes the probability of selecting
![]() as the instruction at address
as the instruction at address ![]() ,
given that the first
,
given that the first ![]() instructions have already
been selected.
The probability of a program is the product of the
probabilities of its constituents.
instructions have already
been selected.
The probability of a program is the product of the
probabilities of its constituents.
LS' inputs are ![]() and the representation of
a problem denoted by
and the representation of
a problem denoted by ![]() . LS' output is a program that computes a solution
to the problem if it found any.
In this section, all
. LS' output is a program that computes a solution
to the problem if it found any.
In this section, all
![]() will remain fixed.
LS is implemented as a sequence of longer and longer phases:
will remain fixed.
LS is implemented as a sequence of longer and longer phases:
Levin search(problem ![]() , probability matrix
, probability matrix ![]() )
)
(1) Set, the number of the current phase, equal to 1. In what follows, let
denote the set of not yet executed programs
satisfying
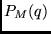
.
(2) Repeat
(2.1) Whileand no solution found do: Generate a program
, and run
until it either halts or until it used up
steps. If
computed a solution for
, return
and exit.
(2.2) Set:= 2

until solution found or
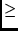
.
Return.
Here ![]() and
and ![]() are prespecified constants.
The procedure above is essentially the same
(has the same order of complexity) as the one
described in the first paragraph of this
section -- see, e.g., [Solomonoff, 1986,Li and Vitányi, 1993].
are prespecified constants.
The procedure above is essentially the same
(has the same order of complexity) as the one
described in the first paragraph of this
section -- see, e.g., [Solomonoff, 1986,Li and Vitányi, 1993].