



Nächste Seite: EINE ZIELFUNKTION FÜR DAS
Aufwärts: PERFORMANZMASSE FÜR DIE DREI
Vorherige Seite: PERFORMANZMASSE FÜR DIE DREI
Inhalt
Wir wollen für den Augenblick annehmen, daß die
Prediktoren 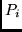 zu allen Zeiten bis zur
Perfektion trainiert werden, was bedeutet, daß
zu allen Zeiten bis zur
Perfektion trainiert werden, was bedeutet, daß
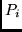 stets
den bedingten Erwartungswert
stets
den bedingten Erwartungswert
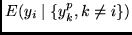 von
von 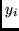 liefert (bei gegebenen Ausgaben der übrigen
Repräsentationsmodule).
Im Falle quasi-binärer Codes ist das folgende
Performanzmaß
liefert (bei gegebenen Ausgaben der übrigen
Repräsentationsmodule).
Im Falle quasi-binärer Codes ist das folgende
Performanzmaß
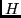 genau dann gleich Null, wenn das
Unabhängigkeitskriterium erfüllt ist:
genau dann gleich Null, wenn das
Unabhängigkeitskriterium erfüllt ist:
![\begin{displaymath}
H = \frac{1}{2} \sum_i \sum_p \left[ P^p_i - \bar{y_i} \right]^2.
\end{displaymath}](img521.png) |
(6.3) |
Dieser Term für wechselseitige Redundanzminimierung zielt darauf ab,
die Ausgaben statistisch voneinander unabhängig zu
machen. Hier existiert eine
Verwandtschaft zu Linskers Dekorrelationsmethode durch
Maximierung der Determinante
der Kovarianzmatrix der Repräsentationsknoten unter Annahme
Gauss-verteilter Signale [49]. Letztere Methode
zielt jedoch lediglich auf die Vermeidung linearer
Abhängigkeiten,
während die Minimierung von (6.3) aufgrund der von
den allgemeinen Prediktoren
modellierbaren Nichtlinearitäten auch
nicht-lineare Redundanz beseitigen kann (sogar
ohne Voraussetzung Gauss-verteilter Eingaben).
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite
![\begin{displaymath}
H = \frac{1}{2} \sum_i \sum_p \left[ P^p_i - \bar{y_i} \right]^2.
\end{displaymath}](img521.png)
![\begin{displaymath}
H = \frac{1}{2} \sum_i \sum_p \left[ P^p_i - \bar{y_i} \right]^2.
\end{displaymath}](img521.png)