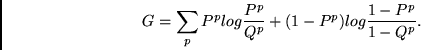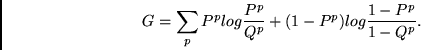Nächste Seite: FAKTORIELLE CODES
Aufwärts: UNÜBERWACHTES LERNEN UND STATISTISCHE
Vorherige Seite: UNÜBERWACHTES LERNEN UND STATISTISCHE
Inhalt
Der G-Max Algorithmus [69]
zielt darauf ab, in den Eingaben enthaltene
Redundanz zu
entdecken. G-Max
maximiert im wesentlichen die Differenz zwischen
der Wahrscheinlichkeitsverteilung 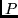 der Ausgaben
eines azyklischen Netzes mit
einem einzelnen binären
probabilistischen
Ausgabeknoten und der
Verteilung
der Ausgaben
eines azyklischen Netzes mit
einem einzelnen binären
probabilistischen
Ausgabeknoten und der
Verteilung  , die man unter der Annahme,
daß die Komponenten der Eingabevektoren
statistisch unabhängig sind, erwarten würde.
Der Ausgabeknoten kann nur die Werte 0 oder 1 annehmen.
Die Wahrscheinlichkeit, daß er in Antwort auf
, die man unter der Annahme,
daß die Komponenten der Eingabevektoren
statistisch unabhängig sind, erwarten würde.
Der Ausgabeknoten kann nur die Werte 0 oder 1 annehmen.
Die Wahrscheinlichkeit, daß er in Antwort auf 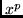 den Wert 1 annimmt, sei mit
den Wert 1 annimmt, sei mit 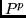 bezeichnet.
Die Wahrscheinlichkeit, daß er in Antwort auf
bezeichnet.
Die Wahrscheinlichkeit, daß er in Antwort auf 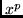 unter der Annahme, daß die Eingabekomponenten statistisch
voneinander unabhängig sind,
den Wert 1 annimmt, sei mit
unter der Annahme, daß die Eingabekomponenten statistisch
voneinander unabhängig sind,
den Wert 1 annimmt, sei mit 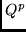 bezeichnet.
Die zu maximierende
Zielfunktion ist die sogenannte asymptotische Divergenz
(oder auch Kullback-Distanz, siehe [44])
bezeichnet.
Die zu maximierende
Zielfunktion ist die sogenannte asymptotische Divergenz
(oder auch Kullback-Distanz, siehe [44])
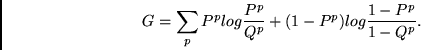 |
(5.8) |
Das Problem des G-Max-Algorithmus besteht darin, daß er
nicht (zumindest nicht in offensichtlicher
Weise) auf mehrdimensionale Ausgaben
erweiterbar ist.
Experimente.
Pearlmutter und Hinton
berichten, daß G-max nach Training mit Bildern
orientierter Balken wie schon
Linskers Methode (Abschnitt 5.2)
ebenfalls zu biologisch plausiblen
`on-center/off-surround'-Strukturen führt
[69].




Nächste Seite: FAKTORIELLE CODES
Aufwärts: UNÜBERWACHTES LERNEN UND STATISTISCHE
Vorherige Seite: UNÜBERWACHTES LERNEN UND STATISTISCHE
Inhalt
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite