



Nächste Seite: MEHRDIMENSIONALE AUSGABEN
Aufwärts: UNÜBERWACHTES LERNEN: ZIELFUNKTIONEN
Vorherige Seite: UNÜBERWACHTES LERNEN: WOZU?
Inhalt
Linskers Infomaxpinzip
[49][50]
zielt auf die Maximierung der
wechselseitigen (Shannon-) Information
[125]
zwischen Ein- und Ausgabeensemble.
Wir setzen eine endliche Zahl von Eingabevektoren 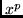 und
Repräsentationsvektoren
und
Repräsentationsvektoren
 voraus. Nach Shannon ist die
wechselseitige Information
zwischen
Ein- und Ausgabe gleich
voraus. Nach Shannon ist die
wechselseitige Information
zwischen
Ein- und Ausgabe gleich
 |
(5.1) |
wobei
 den über das ganze Musterensemble genommenen Durchschnitt
bezeichnet.
den über das ganze Musterensemble genommenen Durchschnitt
bezeichnet.
Es ist keine effiziente Methode zur
Maximierung von (5.1) im Falle beliebiger
azyklischer Netzarchitekturen, beliebiger Ausgabedimensionalität
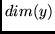 und beliebiger Eingabeensembles bekannt.
und beliebiger Eingabeensembles bekannt.
Betrachtet man allerdings ein Netzwerk, das nur über einen einzigen
Ausgabeknoten
verfügt, dessen Ausgabe  die Summe einer linearen Funktion
des Eingabevektors
die Summe einer linearen Funktion
des Eingabevektors 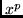 und eines nicht verschwindenden
Rauschterms
und eines nicht verschwindenden
Rauschterms 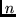 ist,
wobei sowohl die Eingabesignale als auch das Ausgaberauschen
Gauss-Verteilungen unterliegen, so läßt sich eine
kontinuierliche Version von (5.1) als
ist,
wobei sowohl die Eingabesignale als auch das Ausgaberauschen
Gauss-Verteilungen unterliegen, so läßt sich eine
kontinuierliche Version von (5.1) als
 |
(5.2) |
schreiben
[49].
Unter der Annahme, daß  fix bleibt,
läßt sich
fix bleibt,
läßt sich 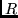 nun ohne weiteres mit der Kettenregel differenzieren.
Der resultierende Lernalgorithmus ist äquivalent
zur Maximierung der Ausgabevarianz.
Interessanterweise stellt dies
eine Variante der Hebbregel dar [33].
nun ohne weiteres mit der Kettenregel differenzieren.
Der resultierende Lernalgorithmus ist äquivalent
zur Maximierung der Ausgabevarianz.
Interessanterweise stellt dies
eine Variante der Hebbregel dar [33].
Wird nun zu jedem Eingabesignal Rauschen mit Varianz
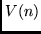 addiert, so ergibt sich nach Linsker
addiert, so ergibt sich nach Linsker
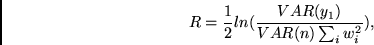 |
(5.3) |
wobei  das Gewicht der Verbindung vom
das Gewicht der Verbindung vom  -ten
Eingabeknoten zum Ausgabeknoten ist.
Der resultierende Lernalgorithmus ist äquivalent
zur Maximierung der Ausgabevarianz unter gleichzeitiger
Minimierung der Länge des Gewichsvektors, was
der Analyse
der prinzipiellen Komponenten des Eingabeensembles enstpricht
(siehe hierzu auch
[65][87][84][126][73]).
-ten
Eingabeknoten zum Ausgabeknoten ist.
Der resultierende Lernalgorithmus ist äquivalent
zur Maximierung der Ausgabevarianz unter gleichzeitiger
Minimierung der Länge des Gewichsvektors, was
der Analyse
der prinzipiellen Komponenten des Eingabeensembles enstpricht
(siehe hierzu auch
[65][87][84][126][73]).
Experimente. [49] berichtet u.a., daß
das Infomaxprinzip
bei unstrukturierten Gauss-verteilten Eingaben
im linearen Fall zu rezeptiven Feldern mit einer
`on-center/off-surround'-Struktur führt, wie sie
auch in biologischen Nervensystemen häufig beobachtet wird.
Unter gewissen Voraussetzungen wurden
auch Kohonen-artige topologische Karten [42]
gefunden [50].
Unterabschnitte




Nächste Seite: MEHRDIMENSIONALE AUSGABEN
Aufwärts: UNÜBERWACHTES LERNEN: ZIELFUNKTIONEN
Vorherige Seite: UNÜBERWACHTES LERNEN: WOZU?
Inhalt
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite
![]() und beliebiger Eingabeensembles bekannt.
und beliebiger Eingabeensembles bekannt.
![]() die Summe einer linearen Funktion
des Eingabevektors
die Summe einer linearen Funktion
des Eingabevektors ![]() und eines nicht verschwindenden
Rauschterms
und eines nicht verschwindenden
Rauschterms ![]() ist,
wobei sowohl die Eingabesignale als auch das Ausgaberauschen
Gauss-Verteilungen unterliegen, so läßt sich eine
kontinuierliche Version von (5.1) als
ist,
wobei sowohl die Eingabesignale als auch das Ausgaberauschen
Gauss-Verteilungen unterliegen, so läßt sich eine
kontinuierliche Version von (5.1) als
![]() addiert, so ergibt sich nach Linsker
addiert, so ergibt sich nach Linsker