Zur Illustration des Subzielgenerierungsprozesses wurde in Zusammenarbeit mit Reiner Wahnsiedler (Diplomand an der TUM) eine in kartesischen Koordinaten definierte zweidimensionale `Miniwelt' konstruiert [139].
Ein `Agent'
kann sich in einer durch ![]() -Achse und
-Achse und ![]() -Achse gegebenen
Ebene reeller Zahlenpaare frei bewegen, so daß die
ausgeführte
Trajektorie (seine `Spur') eine ein-dimensionale Mannigfaltigkeit
in
-Achse gegebenen
Ebene reeller Zahlenpaare frei bewegen, so daß die
ausgeführte
Trajektorie (seine `Spur') eine ein-dimensionale Mannigfaltigkeit
in ![]() darstellt.
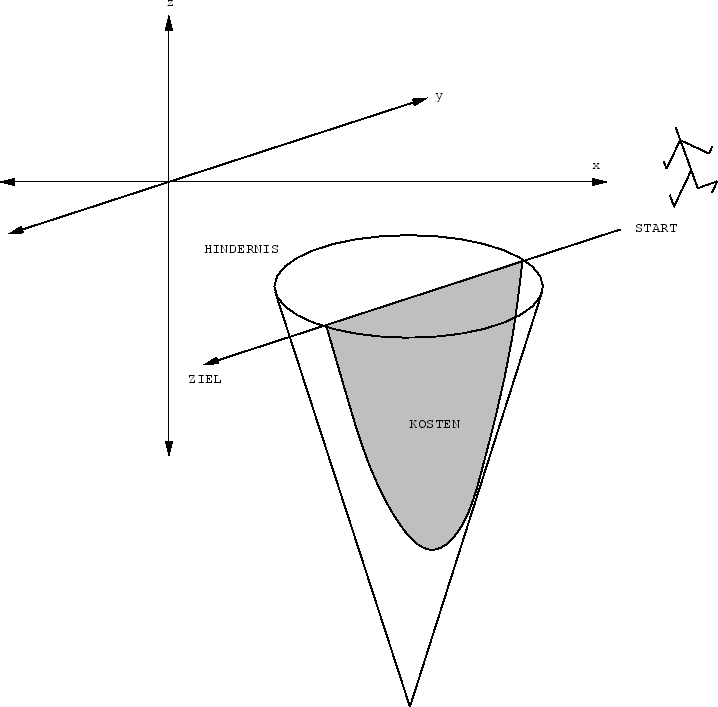
In der Miniwelt existieren allerdings Hindernisse in
Form kreisförmiger `Sümpfe'. Solange sich der
Agent außerhalb der Sümpfe bewegt, entstehen ihm keine
Kosten (in Form negativen reellwertigen Reinforcements).
Der Aufwand, den der Agent zur Querung eines Sumpfes treiben
muß, berechnet sich wie folgt:
darstellt.
In der Miniwelt existieren allerdings Hindernisse in
Form kreisförmiger `Sümpfe'. Solange sich der
Agent außerhalb der Sümpfe bewegt, entstehen ihm keine
Kosten (in Form negativen reellwertigen Reinforcements).
Der Aufwand, den der Agent zur Querung eines Sumpfes treiben
muß, berechnet sich wie folgt:
Der ![]() -te kreisförmige Sumpf
-te kreisförmige Sumpf ![]() mit
Zentrum
mit
Zentrum ![]() und
Radius
und
Radius ![]() bildet die Basis eines in die
durch die
bildet die Basis eines in die
durch die ![]() -Achse definierte dritte Dimension wachsenden
Kegels mit Spitze
-Achse definierte dritte Dimension wachsenden
Kegels mit Spitze
![]() .
Bei gegebener Spur
.
Bei gegebener Spur ![]() sind die durch
sind die durch
![]() verursachten Kosten gleich
verursachten Kosten gleich
| (4.16) |
Des Agenten Aufgabe besteht in der `Planung' einer von einem gegebenen
Startpunkt zu einem gegebenen Endpunkt führenden Aktionssequenz
mit minimalen Kosten.
Für die Experimente wurde angenommen, daß die Kosten aller
Unterprogramme, die zu geradlinigen Bewegungen des Agenten
führen, bereits bekannt sind. Für alle derartigen Unterprogramme
ist (4.16) einfach zu berechnen:
Wieder sei der Startpunkt des ![]() -ten Unterprogramms
-ten Unterprogramms
![]() und sein Zielpunkt
und sein Zielpunkt
![]() .
(4.16) wird damit zur durch den parabelförmigen Kegelschnitt und
der durch den Agenten hinterlassenen Spur definierten
Fläche
.
(4.16) wird damit zur durch den parabelförmigen Kegelschnitt und
der durch den Agenten hinterlassenen Spur definierten
Fläche
| (4.17) |
 |
Als Evaluationsmodul wurde natürlich die bezüglich
Start und Zielpunkt eines Unterprogramms differenzierbare
Summe aller Kosten
| (4.18) |
Die im folgenden gezeigten Abbildungen basieren
auf Rechnerausdrucken in [139].
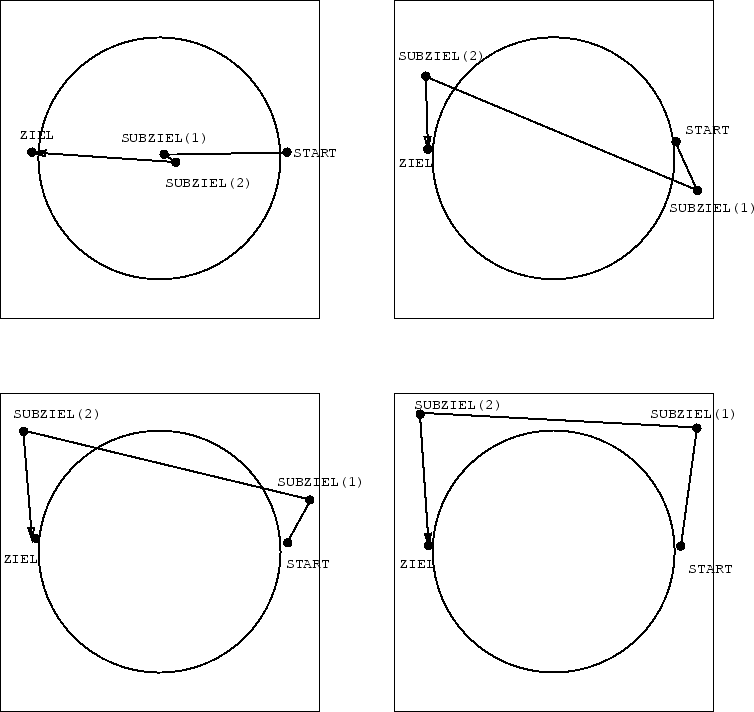
Man betrachte Abbildung 4.6. Ein einzelner Sumpf versperrt
dem Agenten den bereits bekannten geradlinigen Weg vom
Start zum Ziel. Für eine saubere kostenfreie Komposition
einer Lösung aus schon bekannten Unterprogrammen stellen sich
zwei Subziele als zweckmäßig heraus. Für einen statischen
Subzielgenerator (Architektur 1) mit 4 Eingabeknoten und
4 Ausgabeknoten (für zwei
Subziele) erwiesen sich bei 4
versteckten Knoten und einer Lernrate von
![]() drei Iterationsschritte
als ausreichend, um eine befriedigende
Subzielkombination zu finden.
drei Iterationsschritte
als ausreichend, um eine befriedigende
Subzielkombination zu finden.
 |
Der rekurrente Subzielgenerator (Architektur 2) mit 4 Eingabeknoten,
aber nur zwei Ausgabeknoten (dieselben Ausgabeknoten können ja
bei dieser Architektur für verschiedene aufeinanderfolgende
Subziele verwendet werden) stieß
erwartungsgemäß auf etwas größere Schwierigkeiten,
dieselbe Aufgabe zu lösen. Da ein und derselbe Ausgang
von ![]() zu verschiedenen Zeitpunkten verschiedene
kontextabhängige
Subzielrepräsentationen emittieren soll, leidet
Architektur 2 stärker unter dem
altbekannten `cross-talk'-Phänomen als Architektur 1.
Diesem Problem kann man durch Erniedrigung der Lernrate
beikommen, wofür man allerdings in Form von mehr
Trainingsiterationen zahlen muß.
Bei 40 versteckten Knoten und
einer Lernrate von
zu verschiedenen Zeitpunkten verschiedene
kontextabhängige
Subzielrepräsentationen emittieren soll, leidet
Architektur 2 stärker unter dem
altbekannten `cross-talk'-Phänomen als Architektur 1.
Diesem Problem kann man durch Erniedrigung der Lernrate
beikommen, wofür man allerdings in Form von mehr
Trainingsiterationen zahlen muß.
Bei 40 versteckten Knoten und
einer Lernrate von ![]() wurden 22 Iterationsschritte
zur Auffindung einer befriedigenden Lösung
benötigt. Siehe hierzu Abbildung 4.7.
wurden 22 Iterationsschritte
zur Auffindung einer befriedigenden Lösung
benötigt. Siehe hierzu Abbildung 4.7.
Bei mehr als einem Hindernis erwies sich folgende
Initialhilfestellung für den Subzielgenerator
günstiger als eine vorurteilsfreie zufällige
Gewichtsinitialisierung:
Bei gegebener Start/Ziel-Kombination wurde ![]() zunächst
ohne Rücksicht auf etwaige im Wege stehende Sümpfe
daraufhin trainiert, äquidistante Subziele auf der
Start und Ziel verbindenden Linie auszugeben.
Erst danach begann die eigentliche kostenminimierende Lernphase.
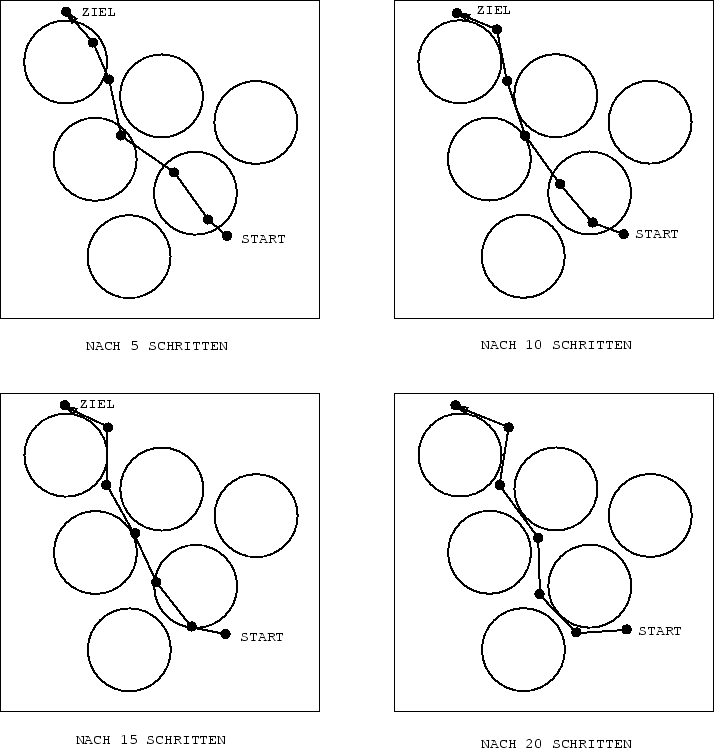
Abbildung 4.8 zeigt die Evolution der aus 4 Subzielen
bestehenden Ausgabe eines wie oben
initialisierten statischen
Subzielgenerators mit 10 Ausgabeknoten, 40 versteckten Knoten
bei einer Lernrate
von
zunächst
ohne Rücksicht auf etwaige im Wege stehende Sümpfe
daraufhin trainiert, äquidistante Subziele auf der
Start und Ziel verbindenden Linie auszugeben.
Erst danach begann die eigentliche kostenminimierende Lernphase.
Abbildung 4.8 zeigt die Evolution der aus 4 Subzielen
bestehenden Ausgabe eines wie oben
initialisierten statischen
Subzielgenerators mit 10 Ausgabeknoten, 40 versteckten Knoten
bei einer Lernrate
von
![]() .
.
Größere Lernraten führten bei diesem Problem zu schlechterer Performanz. Der Grund liegt in der aufgrund der nahe beieinanderliegenden zahlreichen Hindernisse vergleichsweise komplexen Zielfunktion. Je komplexer die Zielfunktion (je kleiner der Einzugsbereich globaler oder lokaler Minima), desto kleiner muß i.a. die Lernarte gewählt werden, und desto mehr Trainingsiterationen sind i.a. erforderlich. Unglücklicherweise gibt es aufgrund der Problemabhängigkeit geigneter Lernraten keine allgemeine Methode zur optimalen Lernrateneinstellung. Die einfachste (und in dieser Arbeit verwendete) Methode zur Auffindung brauchbarer Lernraten besteht von Fall zu Fall im systematischen Probieren.
 |