Die Summe der Gradienten für verschiedene Probleme ![]() ist
gleich dem Gradienten der Summe. Daher genügen uns
für die verschiedenen Architekturen Methoden zur Berechnung
von
ist
gleich dem Gradienten der Summe. Daher genügen uns
für die verschiedenen Architekturen Methoden zur Berechnung
von
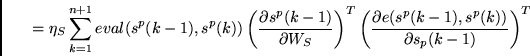 |
(4.9) |
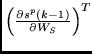 stellt eine Jacobimatrix dar.)
stellt eine Jacobimatrix dar.)
Ist ![]() selbst ein BP-Netzwerk (wie z.B. in
[106]), so verwenden wir
nach Abschluß von
selbst ein BP-Netzwerk (wie z.B. in
[106]), so verwenden wir
nach Abschluß von ![]() 's Trainingsphase
konventionelles BP zur Berechnung von
's Trainingsphase
konventionelles BP zur Berechnung von
| (4.10) |
Für Architektur 1 ist nun die Berechnung von (4.9) nicht mehr
schwierig: Das Fehlersignal für ![]() '
'
![]() -ten Ausgabeknoten
(
-ten Ausgabeknoten
(
![]() ,
,
![]() )
korrespondierend zur
)
korrespondierend zur
![]() -ten
Komponente seines
Ausgabevektors
-ten
Komponente seines
Ausgabevektors
Architektur 2 fordert ein etwas komplexeres, von
BPTT (siehe Kapitel 2) inspiriertes Verfahren.
Falls ![]() ein Ausgabeknoten von
ein Ausgabeknoten von ![]() und
und ![]() ist, so ist das
Fehlersignal für
ist, so ist das
Fehlersignal für
![]() gleich
gleich
| (4.11) |
| (4.12) |
| (4.13) |
| (4.14) |
| (4.15) |
Analog zu BPTT braucht man auch bei obigem Verfahren nicht
![]() vollständige Kopien der beteiligten Netze anzulegen -
es genügt, alle zu den verschiedenen Iterationsschritten
auftretenden Aktivationen zu speichern.
vollständige Kopien der beteiligten Netze anzulegen -
es genügt, alle zu den verschiedenen Iterationsschritten
auftretenden Aktivationen zu speichern.
Wie viele Subziele braucht man für welche Aufgaben? Die einfachste Antwort ist wohl die folgende: Versuche, eine gegebenen Aufgabe zunächst ohne Subziel zu lösen. Falls das nicht klappt, versuche es mit einem Subziel, dann mit zwei, etc. Eine mögliche Erweiterung dieses Versuch/Irrtum-Ansatzes bestünde darin, ein viertes Modul daraufhin zu trainieren, Start/Ziel-Kombinationen auf die minimale Anzahl der benötigten Subziele abzubilden.