



Nächste Seite: ARCHITEKTUR
Aufwärts: WELTMODELLBAUER
Vorherige Seite: WELTMODELLBAUER
Inhalt
Nehmen wir an, ein (später noch genauer zu
spezifizierendes) Steuermodul 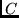 beantwortet den
beantwortet den
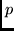 -ten Zustandsvektor
-ten Zustandsvektor 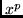 aus der Umgebung mit
einem `Aktionsvektor'
aus der Umgebung mit
einem `Aktionsvektor' 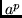 .
Die Umgebung berechnet ihrerseits aus einem Zustandsvektor
.
Die Umgebung berechnet ihrerseits aus einem Zustandsvektor 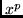 und
einem Aktionsvektor
und
einem Aktionsvektor  mittels einer Evaluationsfunktion
mittels einer Evaluationsfunktion  ein Resultat (z.B. einen neuen Zustand, oder einen Reinforcement-Wert,
oder beides)
ein Resultat (z.B. einen neuen Zustand, oder einen Reinforcement-Wert,
oder beides)
Setzen wir weiterhin voraus, daß ein `distanziertes Performanzmaß'
bestimmte erwünschte Zustandsvektoren 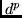 favorisiert.
(Liefert
favorisiert.
(Liefert  beispielsweise `Schmerzsignale' unterschiedlicher
Intensität, so zeichnen sich erwünschte Zustände durch
die Abwesenheit von Schmerz aus.)
Ein sinnvolles derartiges zu minimierendes Performanzmaß ist
beispielsweise `Schmerzsignale' unterschiedlicher
Intensität, so zeichnen sich erwünschte Zustände durch
die Abwesenheit von Schmerz aus.)
Ein sinnvolles derartiges zu minimierendes Performanzmaß ist
mit
Das in diesem Abschnitt zu besprechende Problem
besteht darin, daß  in der Regel unbekannt ist -
man kann aus
in der Regel unbekannt ist -
man kann aus 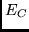 nicht sofort durch Differenzieren
einen Lernalgorithmus herleiten.
Wir haben es nicht mit einfachem überwachten
Lernen zu tun.
nicht sofort durch Differenzieren
einen Lernalgorithmus herleiten.
Wir haben es nicht mit einfachem überwachten
Lernen zu tun.
Eine Lösung des Problems besteht darin,  selbst
durch eine differenzierbare Menge parametrisierter Funktionen
(mit adaptiven Parametern) zu approximieren.
Ein zusätzliches (später noch genauer zu
spezifizierendes) Weltmodell
selbst
durch eine differenzierbare Menge parametrisierter Funktionen
(mit adaptiven Parametern) zu approximieren.
Ein zusätzliches (später noch genauer zu
spezifizierendes) Weltmodell 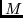 läßt sich dazu verwenden,
die Konkatenation
läßt sich dazu verwenden,
die Konkatenation
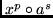 der Vektoren
der Vektoren
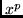 und
und  mit
einem den zu erwartenden geänderten Umgebungszustand
prophezeihenden `Prediktionsvektor'
mit
einem den zu erwartenden geänderten Umgebungszustand
prophezeihenden `Prediktionsvektor' 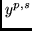 zu beantworten.
Für
zu beantworten.
Für 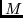 müssen wir dazu ein zweites Hilfs-Performanzmaß einführen:
müssen wir dazu ein zweites Hilfs-Performanzmaß einführen:
Das mit Hilfe von 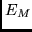 trainierte Modul
trainierte Modul 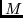 erlaubt uns, wie
bald zu sehen sein wird, die Anwendung der Kettenregel zur
Minimierung der uns eigentlich interessierenden Zielfunktion
erlaubt uns, wie
bald zu sehen sein wird, die Anwendung der Kettenregel zur
Minimierung der uns eigentlich interessierenden Zielfunktion 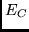 .
.




Nächste Seite: ARCHITEKTUR
Aufwärts: WELTMODELLBAUER
Vorherige Seite: WELTMODELLBAUER
Inhalt
Juergen Schmidhuber
2003-02-20
Related links in English: Recurrent networks - Fast weights - Subgoal learning - Reinforcement learning and POMDPs - Unsupervised learning and ICA - Metalearning and learning to learn
Deutsche Heimseite

![]() in der Regel unbekannt ist -
man kann aus
in der Regel unbekannt ist -
man kann aus ![]() nicht sofort durch Differenzieren
einen Lernalgorithmus herleiten.
Wir haben es nicht mit einfachem überwachten
Lernen zu tun.
nicht sofort durch Differenzieren
einen Lernalgorithmus herleiten.
Wir haben es nicht mit einfachem überwachten
Lernen zu tun.
![]() selbst
durch eine differenzierbare Menge parametrisierter Funktionen
(mit adaptiven Parametern) zu approximieren.
Ein zusätzliches (später noch genauer zu
spezifizierendes) Weltmodell
selbst
durch eine differenzierbare Menge parametrisierter Funktionen
(mit adaptiven Parametern) zu approximieren.
Ein zusätzliches (später noch genauer zu
spezifizierendes) Weltmodell ![]() läßt sich dazu verwenden,
die Konkatenation
läßt sich dazu verwenden,
die Konkatenation
![]() der Vektoren
der Vektoren
![]() und
und ![]() mit
einem den zu erwartenden geänderten Umgebungszustand
prophezeihenden `Prediktionsvektor'
mit
einem den zu erwartenden geänderten Umgebungszustand
prophezeihenden `Prediktionsvektor' ![]() zu beantworten.
Für
zu beantworten.
Für ![]() müssen wir dazu ein zweites Hilfs-Performanzmaß einführen:
müssen wir dazu ein zweites Hilfs-Performanzmaß einführen:

![]() trainierte Modul
trainierte Modul ![]() erlaubt uns, wie
bald zu sehen sein wird, die Anwendung der Kettenregel zur
Minimierung der uns eigentlich interessierenden Zielfunktion
erlaubt uns, wie
bald zu sehen sein wird, die Anwendung der Kettenregel zur
Minimierung der uns eigentlich interessierenden Zielfunktion ![]() .
.