Das hier beschriebene System sollte als on-line Repräsentant einer Menge von Variationen des in Abschnitt 7.5.1 beschriebenen Prinzips angesehen werden.
Tabelle 7.1 liefert einen Überblick über verschiedene zeitabhängige
Aktivationsvektoren, die für die Beschreibung von Architektur
und Algorithmus relevant sind.
![]() , falls ein externer Lehrer zur Zeit
, falls ein externer Lehrer zur Zeit ![]() einen Zielvektor
einen Zielvektor
![]() bereitstellt, und 0 sonst.
Falls
bereitstellt, und 0 sonst.
Falls
![]() gilt, nimmt
gilt, nimmt ![]() einen `Defaultwert'
an, z.B. den Nullvektor.
einen `Defaultwert'
an, z.B. den Nullvektor.
|
A besitzt ![]() Eingabeknoten,
Eingabeknoten,
![]() versteckte Knoten, und
versteckte Knoten, und
![]() Ausgabeknoten (siehe Tabelle 7.1).
Bei reinen Vorhersageproblemen ist
Ausgabeknoten (siehe Tabelle 7.1).
Bei reinen Vorhersageproblemen ist
![]() .
C verfügt über
.
C verfügt über
![]() versteckte Knoten und
versteckte Knoten und
![]() Ausgabeknoten.
Alle Nichtausgabeknoten von
Ausgabeknoten.
Alle Nichtausgabeknoten von ![]() weisen
gerichtete Verbindungen zu allen Nichteingabeknoten von
weisen
gerichtete Verbindungen zu allen Nichteingabeknoten von ![]() auf.
auf.
![]() 's Eingabeknoten besitzen
gerichtete Verbindungen zu allen Nichteingabeknoten von
's Eingabeknoten besitzen
gerichtete Verbindungen zu allen Nichteingabeknoten von ![]() .
Dies ermöglicht
.
Dies ermöglicht ![]() 's Eingabeknoten, zu bestimmten
(kritischen) Zeitpunkten als Eingabeknoten für
's Eingabeknoten, zu bestimmten
(kritischen) Zeitpunkten als Eingabeknoten für ![]() zu fungieren.
Weitere
zu fungieren.
Weitere ![]() Eingabeknoten für
Eingabeknoten für ![]() dienen zur eindeutigen Repräsentation `kritischer' Zeitschritte.
Diesen zusätzlichen Eingabeknoten entspringen
gerichtete Verbindungen zu allen Nichteingabeknoten von
dienen zur eindeutigen Repräsentation `kritischer' Zeitschritte.
Diesen zusätzlichen Eingabeknoten entspringen
gerichtete Verbindungen zu allen Nichteingabeknoten von ![]() .
Schließlich sind alle versteckten Knoten von
.
Schließlich sind alle versteckten Knoten von ![]() Quellen
gerichteter Verbindungen zu allen Nichteingabeknoten von
Quellen
gerichteter Verbindungen zu allen Nichteingabeknoten von ![]() .
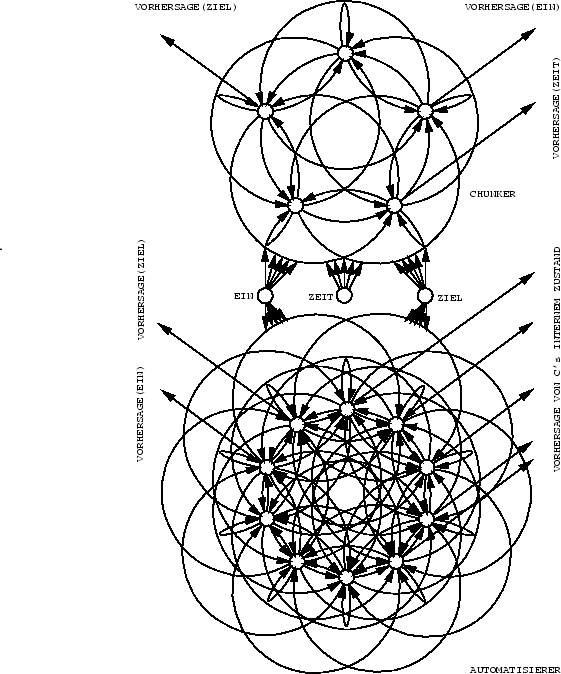
Siehe Abbildung 7.2.
.
Siehe Abbildung 7.2.
 |
Falls ![]() gilt, versucht
gilt, versucht
![]() , seine Vorhersage
, seine Vorhersage
![]() dem Wert
dem Wert ![]() anzugleichen.
Weiterhin bemüht sich
anzugleichen.
Weiterhin bemüht sich ![]() ,
,
![]() zu erreichen und damit
zu erreichen und damit ![]() vorherzusagen.
Hierbei sehen wir das Zielvorhersageproblem wieder als speziellen
Fall eines Eingabevorhersageproblems an.
Ist
vorherzusagen.
Hierbei sehen wir das Zielvorhersageproblem wieder als speziellen
Fall eines Eingabevorhersageproblems an.
Ist ![]() und konnte
und konnte ![]()
![]() nicht korrekt vorhersagen,
so versucht
nicht korrekt vorhersagen,
so versucht ![]() ,
,
![]() zu erreichen.
zu erreichen.
![]() legt es weiterhin darauf an,
legt es weiterhin darauf an,
![]() der nächsten nicht vom Lehrer definierten
Eingabe für
der nächsten nicht vom Lehrer definierten
Eingabe für ![]() gleichzusetzen.
Diese Eingabe mag unter Umständen noch weit in der Zukunft liegen.
Schließlich versucht
gleichzusetzen.
Diese Eingabe mag unter Umständen noch weit in der Zukunft liegen.
Schließlich versucht ![]() ,
,
![]() zu erreichen und damit den Zustand
von
zu erreichen und damit den Zustand
von ![]() zu rekonstruieren. Dies ermöglicht die Kollapsoperation.
Die Aktivationen von
zu rekonstruieren. Dies ermöglicht die Kollapsoperation.
Die Aktivationen von ![]() 's Ausgabeknoten werden dabei als Teil
von
's Ausgabeknoten werden dabei als Teil
von ![]() 's Zustand angesehen.
's Zustand angesehen.
Sowohl ![]() als auch
als auch ![]() werden gleichzeitig durch einen konventionellen
Algorithmus für rekurrente Netze trainiert.
Häufig (siehe z.B. das in Abschnitt 7.4.1 besprochene Experiment)
bietet sich `abgeschnittenes BPTT' an
(siehe Kapitel 2).
werden gleichzeitig durch einen konventionellen
Algorithmus für rekurrente Netze trainiert.
Häufig (siehe z.B. das in Abschnitt 7.4.1 besprochene Experiment)
bietet sich `abgeschnittenes BPTT' an
(siehe Kapitel 2).
Die (inzwischen geläufige) Aktualisierungsprozedur für jedes der beteiligten rekurrenten Netze sieht wie folgt aus:
Wiederhole für eine konstante Iterationsanzahl (typischerweise 1 oder 2):

Nun die Details des Ein-/Ausgabeverhaltens und der zu minimierenden Zielfunktionen (in pseudo-algorithmische Form gefaßt):
