Wir konstruieren eine stochastische Grammatik, i.e. eine
Grammatik, bei der die Anwendung jeder Produktionsregel mit
einer von vornherein festgelegten Wahrscheinlichkeit stattfindet.
Produziert Zeichenkette ![]() die Zeichenkette
die Zeichenkette ![]() mit
Wahrscheinlichkeit
mit
Wahrscheinlichkeit ![]() , so schreiben wir formal
, so schreiben wir formal
Die Grammatik ![]() sei wie folgt definiert (Regeln werden durchnumeriert):
sei wie folgt definiert (Regeln werden durchnumeriert):
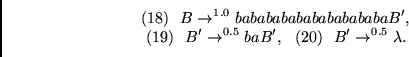 |
(7.5) |
![]() erzeugt eine unendliche Menge von Zeichenreihen,
von denen jede mindestens die Länge
erzeugt eine unendliche Menge von Zeichenreihen,
von denen jede mindestens die Länge
![]() aufweist. Das erste Terminalsymbol jeder Zeichenkette
ist entweder
aufweist. Das erste Terminalsymbol jeder Zeichenkette
ist entweder ![]() oder
oder ![]() . Dann folgt eine sehr lange
aus
. Dann folgt eine sehr lange
aus ![]() 's und
's und ![]() 's bestehende Unterkette.
Das letzte Terminalzeichen ist 1, falls das erste Terminalzeichen
's bestehende Unterkette.
Das letzte Terminalzeichen ist 1, falls das erste Terminalzeichen ![]() war, und 2 sonst.
war, und 2 sonst.
Wir nennen die am Ende jeder Zeichenreihe
auftretenden Symbole ![]() und
und ![]() `Sequenzklassifikatoren'.
Ziel unseres Systems soll die richtige Vorhersage der
Sequenzklassifikatoren sein, ohne sie tatsächlich beobachtet zu haben.
Um dies zu erreichen, muß das System
Ereignisse berücksichtigen, die zumindest 1200 Zeitschritte in
der Vergangenheit zurückliegen.
`Sequenzklassifikatoren'.
Ziel unseres Systems soll die richtige Vorhersage der
Sequenzklassifikatoren sein, ohne sie tatsächlich beobachtet zu haben.
Um dies zu erreichen, muß das System
Ereignisse berücksichtigen, die zumindest 1200 Zeitschritte in
der Vergangenheit zurückliegen.
Zunächst wurde wieder ein konventionelles rekurrentes Netz
getestet.
Die 6 verschiedenen Terminalzeichen wurden jeweils
durch einen Bitvektor der Länge 6 mit einer einzigen
Komponente ![]() repräsentiert. Auch die
Netzwerkausgaben (die Vorhersagen) waren demgemäß 6-dimensional.
repräsentiert. Auch die
Netzwerkausgaben (die Vorhersagen) waren demgemäß 6-dimensional.
Dem konventionellen Netzwerk war es
mit verschiedenen Anzahlen versteckter Knoten,
verschiedenen Lernraten, und verschiedenen Gewichtsinitialisierungen
zwischen -0.5 und 0.5 (wie nach den Experimenten aus dem
letzten Unterabschnitt erwartet) nicht möglich, innerhalb von
![]() Trainingssequenzpräsentationen die Sequenzklassifikatoren
korrekt vorherzusagen.
Ich vermute, daß auch
Trainingssequenzpräsentationen die Sequenzklassifikatoren
korrekt vorherzusagen.
Ich vermute, daß auch
![]() Trainingssequenzpräsentationen nicht ausgereicht hätten -
mangelnde Rechenzeit verhinderte allerdings die Bestätigung dieses
Verdachts.
Trainingssequenzpräsentationen nicht ausgereicht hätten -
mangelnde Rechenzeit verhinderte allerdings die Bestätigung dieses
Verdachts.
Ein Multiebenensystem hingegen traf
bei der Lösung der Aufgabe
auf keine nennenswerten Schwierigkeiten.
Es wurde
eine aus drei Ebenen bestehende Prediktorenhierarchie
verwendet. Alle drei Prediktoren ![]() ,
, ![]() ,
, ![]() ließen sich als rekurrente Netze implementieren, die durch `abgeschnittenes
BPTT' (siehe Kapitel 2)
trainiert wurden, wobei die zu jedem Zeitschritt jeder
Zeitskala auftretenden Fehlersignale lediglich
3 Zeitschritte (!) `in die Vergangenheit' zurückpropagiert wurden
(mehr waren bei diesem Experiment nicht nötig).
Alle 3 Prediktoren besaßen jeweils 6 Eingabeknoten, je einen
für die 6 verschiedenen Terminalzeichen
(für das Experiment waren keine eindeutigen
Zeitschrittrepräsentationen erforderlich).
Als deterministische Ausgabe jedes Prediktors
ließen sich als rekurrente Netze implementieren, die durch `abgeschnittenes
BPTT' (siehe Kapitel 2)
trainiert wurden, wobei die zu jedem Zeitschritt jeder
Zeitskala auftretenden Fehlersignale lediglich
3 Zeitschritte (!) `in die Vergangenheit' zurückpropagiert wurden
(mehr waren bei diesem Experiment nicht nötig).
Alle 3 Prediktoren besaßen jeweils 6 Eingabeknoten, je einen
für die 6 verschiedenen Terminalzeichen
(für das Experiment waren keine eindeutigen
Zeitschrittrepräsentationen erforderlich).
Als deterministische Ausgabe jedes Prediktors ![]() wurde
derjenige Bitvektor der Länge 1 angesehen, der
der eigentlich reellwertigen Ausgabe von
wurde
derjenige Bitvektor der Länge 1 angesehen, der
der eigentlich reellwertigen Ausgabe von ![]() am nächsten war.
Jeder Prediktor verfügte über 3 versteckte Knoten.
Alle Gewichte wurden zufällig zwischen -0.1 und 0.1
initialisiert.
am nächsten war.
Jeder Prediktor verfügte über 3 versteckte Knoten.
Alle Gewichte wurden zufällig zwischen -0.1 und 0.1
initialisiert.
Zunächst wurde ![]() mittels 333 gemäß (7.6) generierter
Trainingssequenzen trainiert (weniger hätten auch gereicht).
Nach Einfrieren von
mittels 333 gemäß (7.6) generierter
Trainingssequenzen trainiert (weniger hätten auch gereicht).
Nach Einfrieren von ![]() 's
Gewichten fand
's
Gewichten fand ![]() 's
Trainingsphase mit ebenfalls 333 Sequenzpräsentationen statt.
Schließlich dienten 333 Sequenzen zur Adjustierung von
's
Trainingsphase mit ebenfalls 333 Sequenzpräsentationen statt.
Schließlich dienten 333 Sequenzen zur Adjustierung von
![]() 's Gewichten. Alle drei Netze verwendeten eine Lernrate
von 0.333. Die insgesamt 999 Sequenzpräsentationen
genügten, dem System beizubringen,
die Sequenzklassifikatoren korrekt vorherzusagen.
's Gewichten. Alle drei Netze verwendeten eine Lernrate
von 0.333. Die insgesamt 999 Sequenzpräsentationen
genügten, dem System beizubringen,
die Sequenzklassifikatoren korrekt vorherzusagen.
![]() lernte im wesentlichen, daß
lernte im wesentlichen, daß ![]() normalerweise von
normalerweise von
![]() gefolgt wird, und umgekehrt. Dies entspricht der lokalen
in den Regeln (15) - (20) enthaltenen Struktur.
Da allerdings dank der Regeln (1) - (14)
die von
gefolgt wird, und umgekehrt. Dies entspricht der lokalen
in den Regeln (15) - (20) enthaltenen Struktur.
Da allerdings dank der Regeln (1) - (14)
die von ![]() vorhergesagten Werte glegentlich falsch sind (manchmal
treten 2
vorhergesagten Werte glegentlich falsch sind (manchmal
treten 2 ![]() 's oder 2
's oder 2 ![]() 's in Folge auf, oder auch eines
der Zeichen
's in Folge auf, oder auch eines
der Zeichen ![]() ),
bekam
),
bekam ![]() durchschnittlich alle 21 Zeitschritte (auf
durchschnittlich alle 21 Zeitschritte (auf ![]() 's Skala)
eine von
's Skala)
eine von ![]() unerwartete Eingabe.
unerwartete Eingabe.
![]() lernte nun seinerseits die in seinen Eingaben
enthaltene durch die Regeln (9) - (14) gegebene `globalere Struktur'.
Die einzigen von
lernte nun seinerseits die in seinen Eingaben
enthaltene durch die Regeln (9) - (14) gegebene `globalere Struktur'.
Die einzigen von ![]() unerwarteten Ereignisse bestanden
nun in die Anfängen und Enden der präsentierten Sequenzen.
Für
unerwarteten Ereignisse bestanden
nun in die Anfängen und Enden der präsentierten Sequenzen.
Für ![]() war es schließlich einfach, die nach den Regeln (1) - (8)
existierende Beziehung
zwischen Sequenzanfängen und -enden zu entdecken und
die Sequenzklassifikatoren korrekt vorherzusagen.
Weitere vergleichbare Experimente finden sich in [37].
war es schließlich einfach, die nach den Regeln (1) - (8)
existierende Beziehung
zwischen Sequenzanfängen und -enden zu entdecken und
die Sequenzklassifikatoren korrekt vorherzusagen.
Weitere vergleichbare Experimente finden sich in [37].
Testaufgaben wie die soeben beschriebene zeigen, daß auf dem Prinzip der Geschichtskompression basierende Systeme in gewissen Trainingsumgebungen mindestens 1000 mal schneller lernen können als konventionelle rekurrente Netze. Dabei ist dies noch eine sehr vorsichtige Abschätzung - aufgrund mangelnder Rechnerzeit war es nicht möglich, herauszufinden, wie lange ein konventionelles Netz zur Lösung obiger Aufgabe braucht. Weiterhin kann es sein, daß (wie im obigen Experiment) die an der Hierarchie beteiligten Prediktoren wesentlich weniger Operationen pro Zeitschritt benötigen als ein konventionelles rekurrentes Netzwerk - einfach deswegen, weil sie auf ihrer gedehnten Zeitskala Fehler häufig nur relativ wenige Zeitschritte in die Vergangenheit zurückpropagieren müssen. In gewissen Umgebungen reichen also lokale Lernalgorithmen aus, um in der Hierarchie beliebig lange Zeitspannen zu überbrücken. In solchen Fällen lassen sich demnach zwei Fliegen mit einer Klappe schlagen.
Es sollte nun klar sein, daß man durch Wahl komplexerer Grammatiken als (7.6) die Vorteile einer Prediktorenhierarchie im Vergleich zu den `konventionellen' Verfahren aus Kapitel 2 beliebig deutlich herausstellen kann - die hier an einem speziellen Beispiel demonstrierte mindestens 1000-fache Überlegenheit der neuen Methodik stellt bei weitem keine obere Schranke dar.