Der Anfangszustandsvektor ![]() der
Repräsentationsknoten sei für alle Sequenzen
der
Repräsentationsknoten sei für alle Sequenzen ![]() der gleiche.
Der Eingabevektor zur Zeit
der gleiche.
Der Eingabevektor zur Zeit ![]() der Sequenz
der Sequenz ![]() sei
die Konkatenation
sei
die Konkatenation
![]() der Eingabe
der Eingabe ![]() und des vorangegangenen internen Zustands
und des vorangegangenen internen Zustands ![]() .
Die Repräsentation des bis zum Zeitpunkt
.
Die Repräsentation des bis zum Zeitpunkt ![]() beobachteten Sequenzpräfixes sei durch
beobachteten Sequenzpräfixes sei durch ![]() selbst gegeben.
selbst gegeben.
Wir minimieren und maximieren im wesentlichen dieselben
Zielfunktionen wie im stationären Fall.
Für den ![]() -ten Repräsentationsknoten,
dem nun rekurrente Verbindungen zu sich selbst
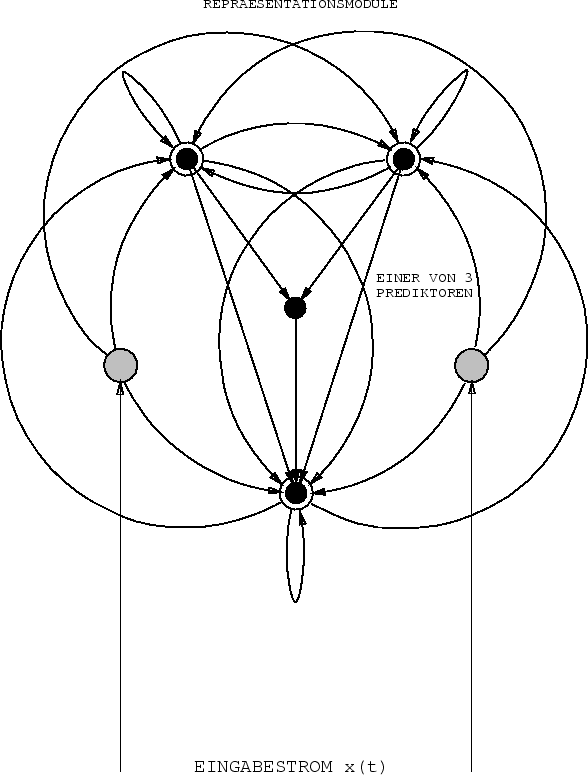
und zu den anderen Modulen entspringen (siehe Abbildung 6.4),
gibt es wieder einen adaptiven Prediktor
-ten Repräsentationsknoten,
dem nun rekurrente Verbindungen zu sich selbst
und zu den anderen Modulen entspringen (siehe Abbildung 6.4),
gibt es wieder einen adaptiven Prediktor
![]() , der seinerseits nicht rekurrent zu sein braucht.
, der seinerseits nicht rekurrent zu sein braucht.
![]() 's Eingabe zur Zeit
's Eingabe zur Zeit ![]() ist
die Konkatenation
der Ausgaben
ist
die Konkatenation
der Ausgaben ![]() aller Repräsentationsknoten
aller Repräsentationsknoten
![]() .
.
![]() 's eindimensionale Ausgabe
's eindimensionale Ausgabe ![]() wird gemäß der Zielfunktion
wird gemäß der Zielfunktion

 |
Die einzige Möglichkeit, die ein Repräsentationsknoten wahrnehmen kann, um sich selbst vor auf den übrigen Repräsentationsknoten beruhenden Voraussagen zu schützen, besteht darin, mittels rekurrenter Verbindungen Eigenschaften der Eingabesequenzen zu speichern, die von den von den übrigen Knoten gespeicherten Aspekten statistisch unabhängig sind.
Um angemessene Gewichtsänderungen zu bestimmen, wird lediglich Information über den Zustand zum lezten Zeitschritt benötigt. Dies hat einen (im Gegensatz zu den ersten drei Methoden aus Kapitel 2) lokalen Algorithmus zur Folge. Trotzdem erlaubt das Verfahren theoretisch, eindeutige Repräsentationen beliebig langer Sequenzen und all ihrer Untersequenzen zu finden - wie sich durch Induktion über die Länge der längsten Eingabesequenz sehen läßt:
1. ![]() kann eindeutige Repräsentationen der
Anfänge aller Sequenzen lernen.
kann eindeutige Repräsentationen der
Anfänge aller Sequenzen lernen.
2. Angenommen, alle Sequenzen und Untersequenzen der
Länge ![]() sind bereits eindeutig in
sind bereits eindeutig in ![]() repräsentiert.
Auch wenn zu jedem Zeitpunkt nur der letzte Zustand, nicht
aber frühere Zustände berücksichtigt werden, kann
repräsentiert.
Auch wenn zu jedem Zeitpunkt nur der letzte Zustand, nicht
aber frühere Zustände berücksichtigt werden, kann
![]() eindeutige Repräsentationen aller
Sequenzen und Subsequenzen
der Länge
eindeutige Repräsentationen aller
Sequenzen und Subsequenzen
der Länge ![]() lernen.
lernen.
Obige Gedankenführung vernachlässigt allerdings mögliche `cross-talk'-Effekte. Die Experimente des nächsten Abschnittes zeigen jedoch die Anwendbarkeit der Methode.